PRISMA EJERCICIOS RESUELTOS PDF
APRENDIZAJES ESPERADOS
• Conocer la definición y características de un prisma.
• Calcular la superficie y volumen de este sólido.
• Conocer la definición y características del tronco de prisma.
• Aplicar lo aprendido en los problemas tipo examen de admisión.
Así como en la geometría plana es muy frecuente el uso de triángulos y cuadriláteros. También en la geometría del espacio hay sólidos cuyo estudio y aplicación a la realidad son muy frecuentes.
Por ejemplo en las construcciones de las casas , edificios , etc. , es muy común ver las columnas de forma prismática o cilíndrica.
También las paredes, los tanques de ciertas cisternas u otros objetos que son de nuestra utilidad.
Con el presente capítulo conoceremos mejor a estas formas geométricas
PRISMA
Un prisma es un poliedro en el cual , dos de sus caras son regiones poligonales congruentes y paralelos denominadas bases y el resto de caras son regiones paralelogramicas denominadas caras laterales.
Las aristas comunes entre las caras laterales y la bases se denominan aristas básicas y las aristas comunes entre las caras laterales se denominan aristas laterales, estas son paralelas y de igual longitud.
NOTACIÓN : Prisma pentagonal ABCDE - FGHIJ ; un prisma es nombrado según él número de lados que tenga su base, así tenemos por ejemplo , si la base tiene seis lados , se denomina prisma hexagonal.
SECCIÓN TRANSVERSAL
Es la sección plana determinada en el prisma por un plano paralelo a su base.
SECCIÓN RECTA
Es la sección determinada en el prisma por un plano perpendicular y secante a todas sus aristas laterales. En todo prisma se realizan los siguientes cálculos.
ÁREA DE SUPERFICIE LATERAL
Es la suma de las áreas de las regiones de todas las caras laterales.
ÁREA DE LA SUPERFICIE TOTAL
Es la suma de las áreas de las regiones de todas las caras.
VOLUMEN
CLASIFICACIÓN
Los prismas se clasifican según la inclinación de su base, en:
PRISMA OBLICUO :
Es aquel prisma cuyas aristas laterales no son perpendiculares a las bases .
PRISMA RECTO :
Es aquel prisma cuyas aristas laterales son perpendiculares a las bases .
PARALELEPÍPEDO :
Es aquel prisma cuya bases son regiones paralelográmicas .
PARALELEPÍPEDO RECTANGULAR RECTOEDRO U ORTOEDRO :
Es aquel Paralelepípedo cuyas caras son regiones rectangulares.
DIAGONAL DE UN PARALELEPÍPEDO:
Es el segmento de recta que une dos vértices no coplanares; todo paralelepípedo tiene cuatro diagonales que se intersectan en su punto medio.
Se clasifica:
1) PARALELEPÍPEDO RECTO:
las bases son paralelogramos y las caras laterales son rectángulos.
2) PARALELEPÍPEDO RECTANGULAR, RECTOEDRO, ORTOEDRO
las seis caras son rectángulos.
3) CUBO O HEXAEDRO REGULAR
las seis caras son cuadrados.
4) ROMBOEDRO
las seis caras son rombos.
PRISMA REGULAR
Es aquel prisma recto cuyas bases son regiones poligonales regulares.
Para construir cajas cúbicas , hexagonales , para empaquetado de artefactos, es necesario realizar el diseño sobre una plancha de cartón y luego realizar el corte correspondiente , tal como se muestra en la figura.
TRONCO DE PRISMA
Es una porción de prisma comprendida entre una de sus bases y un plano no paralelo a las bases, secante a todas sus aristas laterales.
TRONCO DE PRISMA TRIANGULAR OBLICUO
Es aquel determinado en un prisma triangular.
TRONCO DE PRISMA TRIANGULAR RECTO ÁREA DE LA SUPERFICIE LATERAL:
es la suma de las áreas de las caras laterales, las caras laterales son trapecios rectos.
ÁREA DE LA SUPERFICIE TOTAL:
es la suma de las áreas de todas las caras.
VOLUMEN :
es el producto del área de su base por el promedio de sus aristas laterales
VOLUMEN DE UN TRONCO DE PRISMA RECTO TRIANGULAR
El volumen de un tronco de prisma recto de base triangular se calcula multiplicando el área de la base por el promedio de las longitudes de sus aristas.
VOLUMEN DE UN TRONCO DE PRISMA OBLICUO TRIANGULAR :
El volumen de un tronco oblicuo de base triangular se obtiene al multiplicar el área de su base por el promedio de las longitudes de sus alturas .
DESARROLLO DE LA SUPERFICIE DEL PRISMA RECTO
ÁREA LATERAL :
El área lateral de un prisma recto es igual al producto del perímetro de su base por la altura del prisma.
PROPIEDADES GENERALES DE LOS PARALELEPIPEDOS
I) Como las caras opuestas de un paralelepípedo son paralelogramos que tienen sus lados iguales y paralelos dos a dos , dichas caras son iguales y paralelas .
II) Las diagonales de un paralelepípedo se cortan en su punto medio .
III) cualquier plano diagonal que se tome es un paralelogramo y como sus diagonales son las mismas que la del paralelepípedo dichas diagonales del paralelepípedo se cortan en su punto medio.
TEOREMA :
El volumen de un tronco de prisma recto es igual al área de la base multiplicado por el promedio de las aristas del tronco Muchas cajas de cartón tienen a menudo forma de cuboides.
POSTULADO DE BUENAVENTURA CAVALIERI
Si dos sólidos tienen sus bases en dos planos paralelos y sus secciones con todo plano paralelo a los planos de sus bases , tienen áreas iguales , entonces los dos sólidos tienen el mismo volumen.
PROBLEMAS PROPUESTOS
PREGUNTA 1 :
Calcular el volumen de un cubo si su arista mide 4u.
A) 16 u³
B) 64
C) 25
D) 26
E) 28
Rpta. : "B"
PREGUNTA 2 :
Las dimensiones de un rectoedro son 7cm, 6cm y 5 cm. Hallar el volumen del rectoedro .
A) 210cm³
B) 200
C) 180
D) 196
E) 160
Rpta. : "A"
PREGUNTA 3 :
En un paralelepípedo rectangular su diagonal mide 10u y forma un ángulo que mide 45° con la base y un ángulo que mide 30° con una cara lateral , entonces el volumen (en u³) del sólido limitado por el paralelepípedo .
A) 210√2
B) 200√2
C) 180√2
D) 196√2
E) 125√2
Rpta. : "E"
PREGUNTA 4 :
Las dimensiones de un paralelepípedo rectangular son 2x , x y x , el área de su superficie total es igual a 160cm² . hallar el valor de “x”.
A) 1 cm
B) 2 cm
C) 3 cm
D) 4 cm
E) 5 cm
Rpta. : "D"
PREGUNTA 5 :
Con relación a una caja rectangular, el área del fondo, del frente y del lado; es 32cm² , 24cm² y 12cm² respectivamente . Calcular el volumen de la caja .
A) 84 cm³
B) 96
C) 105
D) 120
E) 140
Rpta. : "B"
PREGUNTA 6 :
Calcule el área de la superficie lateral de un tronco de prisma triangular oblicuo, si la sección recta es regular, cuyo lado mide 3 u, y la suma de longitudes de las aristas laterales es 15 u.
A) 40 u²
B) 45 u²
C) 15 u²
D) 60 u²
E) 75 u²
Rpta. : "B"
PREGUNTA 7 :
Calcule el volumen del prisma triangular, si el área de una de sus caras laterales es 50 y la distancia de la arista opuesta a dicha cara lateral es 3.
A) 60
B) 66
C) 68
D) 75
E) 72
Rpta. : "D"
PREGUNTA 8 :
Calcular el área de la superficie total paralelepípedo rectangular , sabiendo que sus dimensiones están en progresión aritmética de razón 4 y su diagonal mide 5√11 .
A) 420
B) 454
C)480
D) 492
E) 512
Rpta. : "B"
PREGUNTA 9 :
Dado un prisma recto, cuya base es un hexágono regular inscrito en un círculo de 8m de radio y cuya altura es igual al diámetro del círculo. Calcular 𝕍/𝔸 en metros, donde 𝔸 es el área lateral y 𝕍 es el volumen del prisma.
A) 2√3
B) 2√2
C) 3√2
D) 5√3
E)√2
Rpta. : "A"
PREGUNTA 10 :
Un tronco de prisma triangular recto tiene por aristas básicas a segmentos cuyas longitudes son 8 ; 12 y 6µ. Las aristas laterales opuestas a estos lados miden 15 ; 5 y 10µ respectivamente, halle el área lateral del tronco.
A) 220 u²
B) 250
C) 270
D) 3000
E) 320
Rpta. : "C"
PREGUNTA 11 :
Un tronco de prisma recto cuya base es un cuadrado ABCD de lado 1m , se levantan perpendicularmente al plano de su base las cuales miden:
AE= 3 m; BF= 10 m CG= 9 m y DH= x m . Calcular el volumen del tronco de prisma. (en m³).
A) 36
B) 27
C) 18
D) 6
E) 12
Rpta. : "D"
PREGUNTA 12 :
Una batea de 10 pies de largo y sección trapecial isósceles de altura 2 pies, base inferior 2 pies y base superior 3 pies. Se vierte agua en la batea a una razón constante . Cuando el volumen del agua es de 45/2 pies³. ¿A que altura de la base se encuentra el agua?
A) 2/3
B) 1/4
C) 3/2
D) 1/2
E) 1
Rpta. : "E"
PREGUNTA 13 :
En un triángulo ABC se traza AM y BN, perpendiculares al plano que contiene a dicho triángulo y en el mismo semiespacio. Si BN=2(MA) y S es punto medio de MC, calcule la razón de volúmenes de los sólidos MSBN y ABCM.
A) 1
B) 2/3
C) 1/4
D) 1/2
E) 1/3
Rpta. : "A"
PREGUNTA 14 :
Dado un prisma, calcule la razón entre el número de aristas y el número de caras laterales.
A) 2
B) 1,5
C) 1
D) 2,5
E) 3
Rpta. : "E"
PREGUNTA 15 :
En un prisma hexagonal regular ABCDEF -A'B'C'D'E'F' de volumen 48√3 se ubica M punto medio de DD', si AA'= 8 calcule A'M.
A) 4√2
B) 3
C) 6
D) 5
Rpta. : "A"
PREGUNTA 16 :
En un prisma cuadrangular regular ABCD - EFGH de volumen 216√2 𝑢³ si ACGE es un cuadrado, calcule el área de la superficie lateral.
A) 127√2 𝑢³
B) 144√2 𝑢³
C) 146√2 𝑢³
D) 136√2 𝑢³
E) 196√2 𝑢³
Rpta. : "B"
PREGUNTA 17 :
Se tiene un prisma oblicuo de siete caras. Calcule la suma de ángulos internos de la base del prisma.
A) 540°
B) 900°
C) 840°
D) 720°
E) 680°
Rpta. : "A"
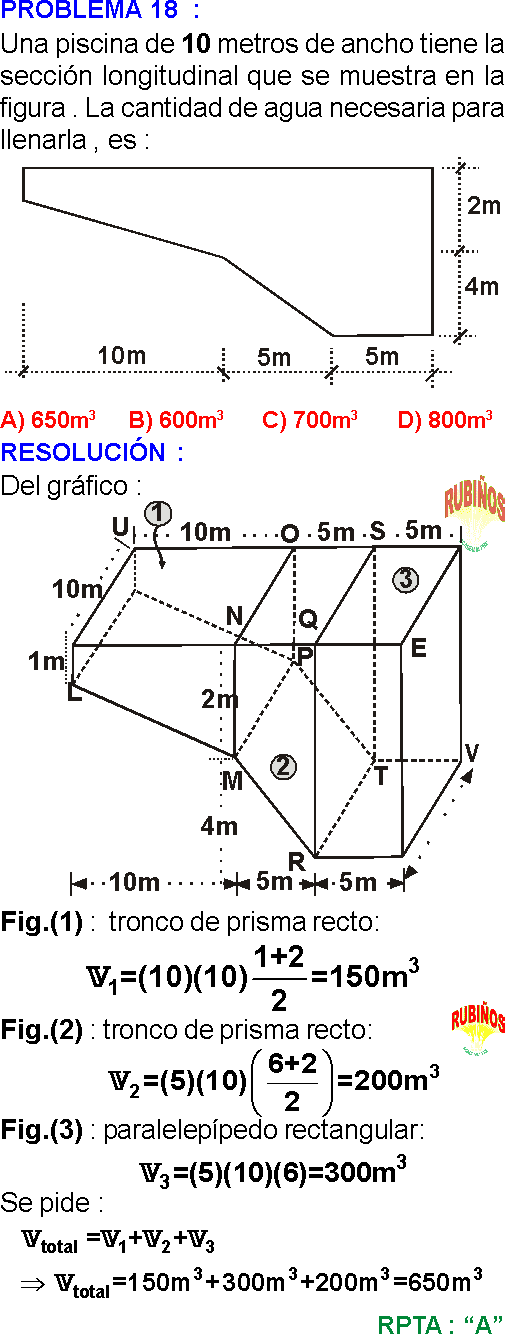
PREGUNTA 18 :
En un hexaedro regular de volumen igual a 27, se traza un plano secante a la superficie lateral que divide al segmento que une los centros de las bases en la razón de 3 a 2. Calcule el volumen del tronco de prisma cuadrangular de menor volumen que se ha formado.
A) 24/5
B) 14/5
C) 32/5
D) 54/5
E) 43/5
Rpta. : "D"
PREGUNTA 19 :
Indique la secuencia correcta de verdad (V) o falsedad (F) respecto a los siguientes enunciados.
I. En todo prisma, sus bases son paralelas y congruentes.
II. En un prisma regular, sus aristas laterales son iguales con las aristas básicas.
III. En todo prisma, el número de aristas básicas es el doble del número de aristas laterales.
A) VVV
B) VFV
C) VFF
D) FVV
E) FVF
Rpta. : "B"
PREGUNTA 20 :
Un tronco de prisma triangular regular, ABC - DEF, la base regular ABC tiene área igual a 16. Si la distancia entre los centroides es igual a 12, calcule el volumen de dicho sólido.
A) 191
B) 192
C) 193
D) 102
E) 125
Rpta. : "B"
PREGUNTA 21 :
Se tiene una región equilátera ABC cuyo lado mide √3; hacia el mismo semiespacio, por A y B, se levantan las perpendiculares al plano AE=2 y BF=6. Calcule el volumen del sólido ABCEF.
A) 4 𝑢³
B) 3√2 𝑢³
C) 3 𝑢³
D) 2√3 𝑢³
E) 2 𝑢³
Rpta. : "D"
PREGUNTA 22 :
En un tronco de prisma triangular oblicuo, la longitud del segmento que une los baricentros de sus bases es 16. Calcule la longitud de la menor arista, si estas están en razón de 3, 4 y 5.
A) 4
B) 12
C) 48
D) 16
E) 8
Rpta. : "B"
PREGUNTA 23 :
Se tiene un prisma cuadrangular regular ABCD-EFGH, tal que AC=6 y m∢ EDG = 74º. Calcule el área de la superficie lateral del prisma.
A) 8√7 𝑢²
B) 4√14 𝑢²
C) 16√7 𝑢²
D) 12√14 𝑢²
E) 32√7 𝑢²
Rpta. : "D"
PREGUNTA 24 :
En un tronco de prisma regular ABCD-EFGH, la base ABCD es una región cuadrada de lado igual a 6. Si AE= 3 y CG= 8, calcule el volumen del tronco.
A) 198 𝑢³
B) 186 𝑢³
C) 200 𝑢³
D) 210 𝑢³
E) 236 𝑢³
Rpta. : "A"
PROBLEMAS RESUELTOS
PREGUNTA 1 :
El desarrollo lateral de un prisma cuadrangular regular es un cuadrado de lado 18 m. Calcula el volumen del prisma.
A) 360,5 m³
B) 362,5 m³
C) 364,5 m³
D) 371,6 m³
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 2 :
Colocando cinco cubos verticalmente, se determina un prisma de diagonal 18; calcula el área total del prisma.
A) 216 u²
B) 172 u²
C) 241 u²
D) 264 u²
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 3 :
En un prisma regular ABCD-EFGH cuya arista básica mide 4m y P es punto medio de CG.
Si AP = 2√17 m, calcule (en m²) el área de la superficie total del prisma.
A) 112
B) 224
C) 256
D) 290
E) 178
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 4 :
Si con un galón de pintura se pintan 30m². ¿Cuántos galones se necesitarán para pintar las paredes de una habitación que tiene por dimensiones 20 m, 10 m y 3 m respectivamente, si la habitación tiene una puerta de 1,5m×2m, una ventana de 8,5m×2m y dos ventanas de 2,5 m×2 m?
A) 1
B) 3
C) 4
D) 5
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 5 :
En un prisma hexagonal regular, la arista lateral es el doble de su arista básica y el volumen del prisma es 24√3 u³. Calcule el área lateral del prisma.
A) 36 u²
B) 64 u²
C) 40 u²
D) 50 u²
E) 48 u²
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 6 :
Un acuarista elaboró un novedosos acuario, cuya base es un hexágono de 10 cm de arista, y una altura de 15 cm. Halle la cantidad de vidrio que utilizó:
A) (900 + 150√3) cm²
B) 800 cm²
C) 1800 cm²
D) 1000 cm²
E) 700√3 cm²
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 7 :
En un prisma hexagonal regular, la arista lateral es el doble de su arista básica, si su volumen es 24√3 . Calcule el área de su superficie lateral.
A) 56u²
B) 36u²
C) 48u²
D) 64u²
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 8 :
Se tiene un terreno PQR, QR=8, QP=6, PR=10, luego se levanta las perpendiculares ⊥PN, ⊥QS y ⊥RT, PN=3, QS=10 y RT=5. Calcule el área de la malla que limita el terreno formado por las perpendiculares.
A) 139
B) 143
C) 131
D) 157
E) 128
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 9 :
En un prisma hexagonal regular ABCDEF-GHIJKL, se inscribe una pirámide regular tal que su base coincide con la base ABCDEF y su vértice coincide con el centro de la base superior. La arista lateral de la pirámide mide 20 u y forma con el plano de la base un ángulo cuya medida es 60º. Calcule el volumen del Prisma.
A) 3 500 u³
B) 4 200 u³
C) 4 000 u³
D) 5 200 u³
E) 4 500 u³
RESOLUCIÓN :
Rpta. : "E"
