MÁXIMOS Y MÍNIMOS RELATIVOS USANDO DERIVADAS Y PUNTOS CRITICOS EJERCICIOS RESUELTOS PDF

• CLICK AQUI VER PDF 1  
• VER PDF 2 

MÁXIMOS Y MÍNIMOS RELATIVOS DE UNA FUNCIÓN 

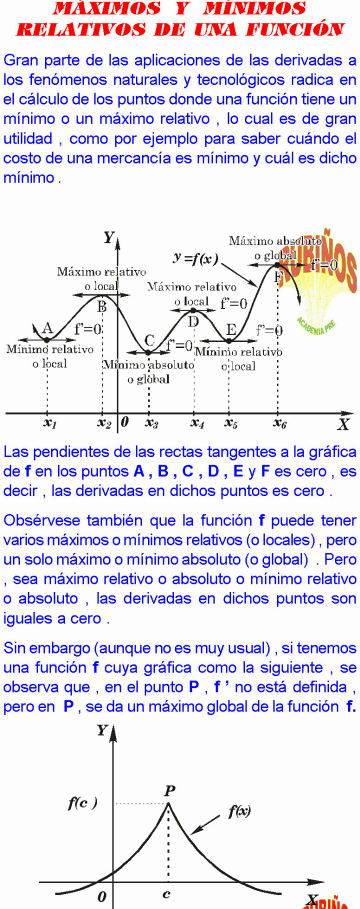
Gran parte de las aplicaciones de las derivadas a los fenómenos naturales y tecnológicos radica en el cálculo de los puntos donde una función tiene un mínimo o un máximo relativo , lo cual es de gran utilidad , como por ejemplo para saber cuándo el costo de una mercancía es mínimo y cuál es dicho mínimo . 

Las pendientes de las rectas tangentes a la gráfica de f en los puntos A , B , C , D , E y F es cero , es decir , las derivadas en dichos puntos es cero . 

Obsérvese también que la función f puede tener varios máximos o mínimos relativos (o locales) , pero un solo máximo o mínimo absoluto (o global) . 

Pero , sea máximo relativo o absoluto o mínimo relativo o absoluto , las derivadas en dichos puntos son iguales a cero . Sin embargo (aunque no es muy usual) , si tenemos una función f cuya gráfica como la siguiente , se observa que , en el punto P , f ’ no está definida , pero en P , se da un máximo global de la función f. En esta sección vamos a dedicarnos a calcular los máximos y mínimos de funciones con diferentes propósitos. En muchas situaciones de la vida real se requiere de la optimización de una cantidad. Otras veces, la naturaleza opera de manera que minimiza algo, por ejemplo, la electricidad siempre pasa a través del medio que ofrece mínima resistencia, la luz, al pasar de un medio a otro, siempre sigue una trayectoria que hace minimo el tiempo de trayecto de un punto a otro, etc. 

En este tipo de problemas siempre es recomendable primero identificar la variable que se desea minimizar (o maximizar), luego hacer l.ID modelo matemático del problema relacionando las variables que están involucradas en el problema. 

Después optimizar (minimizar o maximizar) la cantidad que deseamos. 

PROBLEMAS DE MÁXIMOS Y MÍNIMOS. 

Los métodos para determinar los máximos y mínimos de las funciones se pueden aplicar a la solución de problemas prácticos, para resolverlos tenemos que transformar sus enunciados en fórmulas, funciones o ecuaciones. Debido a que hay múltiples tipos de ejercicios no hay una regla única para sus soluciones, sin embargo puede desarrollarse una estrategia general para abordarlos, la siguiente es de mucha utilidad. 

ESTRATEGIA PARA RESOLVER 

PROBLEMAS APLICADOS A LA OPTIMIZACIÓN. 

a) Identificar los hechos dados y las cantidades desconocidas que se tratan de encontrar. 

b) Realizar un croquis o diagrama que incluya los datos pertinentes introduciendo variables para las cantidades desconocidas. 

c) Enunciar los hechos conocidos y las relaciones entre las variables. 

d) Determinar de cuál de las variables se desea encontrar el máximo o el mínimo y expresa resta variable como función de una de las otras variables. 

e) Encontrar los valores críticos de la función obtenida. 

f) Utilizar el criterio de la primera o de la segunda derivada para determinar si esos valores críticos son máximos o mínimos. 

g) Verificar si hay máximos o mínimos en la frontera del dominio de la función que se obtuvo anteriormente.

 h) MUCHA DEDICACIÓN Y PRÁCTICA. 

1.) Hallar dos números cuya suma es 18, sabiendo que el producto de uno por el cuadrado el otro es máximo. Ejemplo 1 : Determinar los puntos críticos de la función : f(x) = x2 – 6x + 7 Resolución : Derivando la función resulta : f’(x) = 2x – 6 Como f ’(x) existe para todo x , entonces los únicos puntos críticos de f(x) son aquellos en que f ’ (x) se hace cero . f ’ (x) = 0 2x – 6 = 0 x = 3 Ejemplo 2 : Determinar los puntos críticos de la función : f(x) = 2x3 – 6x2 – 18x + 1 Resolución : Hallamos la derivada de la función : f ’ (x) = 6x2 – 12x – 18 Igualamos a cero dicha derivada : f ’(x) = 6x2 – 12x – 18 = 0 6(x2 – 2x – 3) = 0 6(x – 3)(x + 1) = 0 x = 3 ; x = 1 ...(puntos críticos) OBSERVACIONES : I) Una función puede carecer de puntos críticos. Ejemplo : Sea : f(x) = 3x + 5 f ’(x) = 3 f ’(x) = 3 = 0 x0 “En ningún lugar del dominio la pendiente de la función se hace cero” II) Una función puede tener infinitos puntos críticos Ejemplo : Sea: f(x) = sen x f ’ (x) = cos x f ’ (x) = cos x = 0 “En todos los puntos de abscisa : la pendiente se hace cero” Ejemplo 3 : Consideremos la función f(x) = x3 ; . La gráfica de f se muestra en la figura adjunta . Es claro que f’(0) = 0 , de lo cual se sigue que 0 es un punto crítico de f . Sin embargo , 0 no es punto de extremo local de f . Comentario : “El punto crítico puede ocurrir para un extremo relativo máximo o un extremo relativo mínimo” En A: ocurre un valor crítico x0 que determina un extremo máximo relativo . En B : ocurre un valor crítico x0 que determina un extremo mínimo relativo . Mínimo y máximo relativo El número f(c) es un mínimo relativo de la función f , si existe un intervalo ]a ; b[ que contiene a c, tal que para todo . Si f(x) < f(c). entonces f(c) es un máximo relativo de la función en f . Al menor de todos los mínimos relativos en [a ; b] se le llama mínimo absoluto y al mayor , máximo absoluto . Si f está difinida en un intervalo I , y si c es un número del dominio , tal que f ’(c) = 0 ó f ’ (c) no existe o c es uno de los extremos del intervalo I (si es que fuese cerrado) ; entonces decimos que c es un punto crítico de la función f . Del gráfico anterior, podemos deducir que para la existencia de un máximo o mínimo de una función , esta debe ser continua en un intervalo cerrado . Así tenemos el siguiente teorema : Teorema de la existencia Sea f una función continua en un intervalo cerrado [a ; b] , entonces f tiene un máximo y un mínimo en dicho intervalo . Ahora nos preguntamos : ¿cómo podemos calcular los mínimos y máximos relativos y/o absolutos de una función en un intervalo dado? Para entender esto , basta con dar una chequeada a la gráfica anterior y podemos concluir : “Para encontrar máximos y/o mínimos relativos de una función continua f , es un punto crítico x = c , basta con que la función sea creciente por un lado de ‘‘c’’ y decreciente por el otro (o viceversa)”. Esto trae consigo el siguiente teorema.