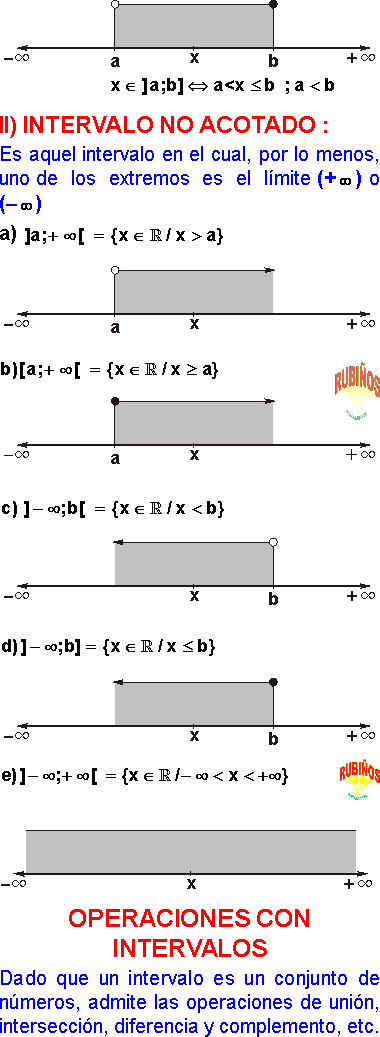OPERACIONES CON INTERVALOS EJERCICIOS RESUELTOS EN PDF Y VIDEOS
intervalos ejercicios resueltos pdf operaciones con intervalos ejercicios resueltos pdf operaciones con intervalos ejercicios propuestos ejercicios resueltos de intervalos abiertos cerrados y semiabiertos notacion de intervalos ejercicios resueltos intervalos infinitos ejercicios resueltos ejercicios de intervalos abiertos y cerrados ejercicios de intervalos en la vida cotidianaRECTA NUMÉRICA REAL Es una recta geométrica donde se establece una biyección entre los números reales y los puntos de la recta, es decir, a cada punto de la recta le corresponde un único número real y recíprocamente a cada número real le corresponde un único punto de la recta. Por eso se dice biyección o correspondencia biunívoca o perfecta negativos positivos _00 , , ~'--/-+-,_,,_:._.fi-+-, --+-- __ , -2 -1-112 O 1/2 2 3 ... +00 INTERVALO Es un subconjunto del conjunto de los números reales, es decir, es un conjunto formado por números reales definidos por la propiedad de que sus elementos satisfacen ciertas desigualdades. Así representamos la desigualdad a < b sobre la recta numérica: M x N a Se observa que el punto M, que representa al número a, está a la izquierda de N, que representa al número b. Esto nos demuestra que existen números reales entre a y b, o sea a < x y x < b, que se pueden escribir a < x < b; luego diremos que un intervalo es un conjunto de números reales, los cuales se encuentran entre dos extremos a los que denominaremos extremo inferior y extremo superior. Asimismo, existen dos tipos de intervalos: los acotados "Nota Si a=b ---7 (a; b)={ }= (Es el conjunto vacío) li>Nota S· b {[a; b]={a} I 0= ---7 (a; b) = Intervalos acotados Un intervalo se dice acotado si sus extremos son finitos. Entre ellos tenemos: Intervalo abierto El intervalo abierto está determinado por dos números a y b, donde a S b. Es el conjunto de todos los números x E lRpara los que a < x < b. Notación: (a; b) o la; b[ Matemáticamente: (a; b)={x E lR/ a < x < b} x a b Intervalo cerrado El intervalo cerrado está determinado por los extremos a y b, donde a S b. Es el conjunto de todos los números x E lRpara los que a S x S b. Notación: [a; b] Matemáticamente: [a; b]={XE lR/ asxs b} x a b Intervalos semiabiertos o semicerrados Si a S b, los siguientes intervalos se consideran semiabiertos o semicerrados. (a;b]={xE lR/a a} [a; +oo)={x/x ~ a} (-00; a