PIRÁMIDE EJERCICIOS RESUELTOS PDF
APRENDIZAJES ESPERADOS :
• Conocer la definición y características de una pirámide.
• Calcular la superficie y volumen de este sólido.
• Conocer la definición y características del tronco de pirámide.
• Aplicar lo aprendido en los problemas tipo examen de admisión.
Pirámide es una palabra nos recuerda Egipto y los monumentos que ahí sirvieron de tumba a sus faraones.
La más grande de éstas es la de Keops, que data del 2600 a.J.C. aproximadamente y es de base cuadrada y con unas dimensiones impresionantes: 230 m de arista de la base y 146 m de altura. Está formada por 2,3 millones de bloques de piedra, cada uno de los cuales pesa aproximadamente 20 toneladas.
PIRÁMIDE
Es aquel poliedro en el cual una de sus caras es una región poligonal cualquiera denominada base , y sus otras caras son regiones triangulares denominadas caras laterales , todas ellas tienen un vértice en común el cual se le denomina vértice o cúspide de la pirámide.
ÁREA DE LA SUPERFICIE LATERAL
Es la suma de las áreas de las regiones de las caras laterales.
ÁREA DE LA SUPERFICIE TOTAL
Es la suma de las áreas de las regiones de todas las caras.
VOLUMEN
De acuerdo al número de lados de su base ; las pirámides pueden ser triangulares , cuadrangulares pentagonales ,......si su base tiene tres , cuatro , cinco..... lados respectivamente ; tal como se muestra en la siguiente figura.
PIRÁMIDE REGULAR
Es aquella pirámide cuya base está limitada por un polígono regular (triángulo equilátero , cuadrado , pentágono regular, etc.) y, Además, tiene todas sus aristas laterales de igual longitud. En toda pirámide regular las caras laterales son congruentes y el pie de altura es el centro de la base
APOTEMA DE LA PIRÁMIDE REGULAR
Es la altura de cualquiera de sus caras laterales.
Es de notar que el apotema de la pirámide forma, junto con el apotema de la base y la altura de la pirámide, un triángulo rectángulo.
Es la perpendicular trazada del vértice de la pirámide hacia una arista básica .
En toda pirámide regular se cumple:
Las caras laterales están limitados por triángulos isósceles congruentes entre sí.
Las caras laterales y la base forman ángulos diedros de medidas iguales.
Las aristas laterales forman con la base ángulos de medidas iguales.
PIRÁMIDE IRREGULAR
Es aquella que no tiene todas las características de una pirámide regular .
PROPIEDAD :
Si en una pirámide, su base es un polígono inscrito en una circunferencia y la altura cae en el centro de la base , entonces sus aristas laterales serán congruentes.
PROPIEDAD :
La relación de los volúmenes de dos pirámides que tienen la misma altura es igual a la relación de las áreas de las bases.
POSTULADO DE BUENAVENTURA CAVALIERI
Si dos sólidos de igual altura tienen bases iguales equivalentes y las secciones planas determinadas por planos paralelos a las bases , a igual distancia de éstas son polígonos de igual área, entonces dichos sólidos tienen el mismo volumen.
PIRÁMIDES SEMEJANTES
Todo plano secante a una pirámide y paralelo a su base, determina una pirámide parcial semejante al total.
PROPIEDADES :
En dos pirámides semejantes se cumple:
• Sus líneas homólogas son proporcionales.
• Las áreas, de su bases, de sus superficies totales; son proporcionales a los cuadrados de las longitudes de sus líneas homólogas.
• Sus volúmenes son proporcionales a los cubos de las longitudes de sus líneas homólogas.
TEOREMA :
Si se corta una pirámide cualquiera por un plano paralelo a la base se obtiene una pirámide parcial semejante a la pirámide total.
TRONCO DE PIRÁMIDE
Es la porción de pirámide comprendida entre la base y la sección plana determinada por un plano secante a la pirámide y paralelo a su base.
A la base y a dicha sección se le denomina base del tronco de pirámide; su caras laterales son regiones trapeciales, sus bases son regiones poligonales semejantes y su altura es la distancia entre sus bases.
TRONCO DE PIRÁMIDE REGULAR
Es aquel tronco de pirámide cuyas bases son regionales poligonales regulares de modo que sus centros están sobre una misma recta perpendicular a dichas bases.
Sus caras laterales son regionales trapeciales isósceles congruentes entre sí, la altura de cada una de ellas se denomina apotema del tronco de pirámide.
TEOREMA :
Si en una pirámide triangular se traza un plano no paralelo a las bases se forman dos pirámides cumpliéndose que la relación de volúmenes es igual a la relación de los productos de las aristas que concurren en el vértice común .
TRONCO DE PIRÁMIDE REGULAR
Es el sólido que se determina al cortar a una pirámide regular con un plano paralelo a su base. Sus caras laterales son trapecios isósceles iguales.
SUGERENCIAS :
☛ Toda pirámide regular tiene base regular y la proyección de su vértice coincide con el centro de la base.
☛ En las pirámides regulares trabajar con una parte que considere las apotemas de la base y de la pirámide, además de la altura.
PROBLEMAS PROPUESTOS
PREGUNTA 1 :
El área de la superficie lateral de una pirámide cuadrangular regular es 600m², el apotema de la pirámide mide 25m . calcular la longitud de sus aristas básicas.
A) 6cm
B) 12
C) 3
D) 18
E) 14
Rpta. : "B"
PREGUNTA 2 :
¿Cuánto mide el apotema y la altura de una pirámide cuadrangular regular si su arista lateral mide 20 cm y la arista de la base 24 cm?
A) 4√7
B) 2√7
C) √7
D) 3√7
E) 4√5
Rpta. : "A"
PREGUNTA 3 :
En una pirámide triangular, se traza un plano secante y paralelo a su base, tal que biseca a la altura de la pirámide. Calcule la razón de volúmenes de los sólidos determinados.
A) 1/2
B) 1/3
C) 1/5
D) 1/6
E) 1/7
Rpta. : "E"
PREGUNTA 4 :
Una pirámide regular de base cuadrada es equivalente con un cubo. Si la arista del cubo mide 6 y la arista básica de la pirámide mide 9, calcular la altura de la pirámide.
A) 6
B) 12
C) 8
D) 18
E) 10
Rpta. : "C"
PREGUNTA 5 :
En una pirámide cuadrangular regular, una arista básica mide 10 y una arista lateral mide 13. Calcule el área de la superficie lateral de la pirámide.
A) 200 𝑢²
B) 360 𝑢²
C) 260 𝑢²
D) 240 𝑢²
E) 390 𝑢²
Rpta. : "D"
PREGUNTA 6 :
Determinar el volumen de una pirámide hexagonal regular, si su arista lateral mide 6 cm y que ésta forma con la base un ángulo que mide 30°.
A) 81√3/2 𝑢³
B) 2√13
C) 124
D) 96
E) 144
Rpta. : "A"
PREGUNTA 6 :
El volumen de un tronco de pirámide es 208 𝑢³, su altura 12 y el área de una de sus bases 36 𝑢². Calcule el área de la otra base.
A ) 3 𝑢²
B) 4 𝑢²
C) 8 𝑢²
D) 9 𝑢²
E) 6 𝑢²
Rpta. : "B"
PREGUNTA 7 :
Se tiene una pirámide regular cuadrangular V - ABCD cuyo volumen es 125 𝑐𝑚³, en VC se ubica el punto M tal que 3VM= 2(MC). Calcule el volumen de la pirámide M - ABCD.
A) 60 𝑐𝑚³
B) 100 𝑐𝑚³
C) 75 𝑐𝑚³
D) 90 𝑐𝑚³
E) 45 𝑐𝑚³
Rpta. : "C"
PREGUNTA 8 :
En un tronco de pirámide triangular regular, los inradios de las bases miden 1 y 2. Calcule el área de la superficie lateral si el apotema del tronco mide 3.
A) 48√3 𝑢²
B) 54 √3 𝑢²
C) 27√3 𝑢²
D) 36√3 𝑢²
E) 52√3 𝑢²
Rpta. : "C"
PREGUNTA 9 :
En una pirámide regular P - ABCDEF, O es centro de la base ABCDEF, tal que m∢PBO= 45° y AB= 2. Calcule el volumen de esta pirámide.
A) 6√3 𝑢³
B) 4√3 𝑢³
C) 5√3 𝑢³
D) 8√3 𝑢³
E) 7√3 𝑢³
Rpta. : "B"
PREGUNTA 10 :
La altura de un tronco de pirámide cuadrangular regular es 6 m y los lados de las bases miden 1,2m y 4,7m respectivamente. ¿Cuál es la longitud de su apotema?
a) 6,25m
b) 7,5
c) 10,5
d) 5,25
e) 11,25
Rpta. : "A"
PREGUNTA 11 :
En una pirámide cuadrangular regular O-ABCD, su arista básica mide a y su altura mide 2a . Calcule la distancia entre BD y OA .
A) a
B) a/3
C) 2a/5
D) 2a/3
E) a/5
Rpta. : "D"
PREGUNTA 12 :
Una pirámide triangular tiene volumen 120. Calcule el volumen del sólido que tiene como vértices los puntos medios de las aristas .
A) 40
B) 50
C) 60
D) 80
E) 100
Rpta. : "C"
PREGUNTA 13 :
Calcule el área de la superficie lateral de un tronco de pirámide regular ABCD-EFGH si se sabe que m∡FBH= 90°. Su arista lateral mide 2 y determina un ángulo de 60° con la base.
A) 2√7
B) 3√7
C) 4√7
D) 5√7
E) 6√7
Rpta. : "E"
PREGUNTA 14 :
Se tiene un foco iluminado estando a 12m del piso. ¿A cuántos metros del nivel del piso se debe colocar una placa rectangular de 8m de largo y 4m. de ancho para que proyecte una sombra de 288m² , si la vertical del foco pasa por el centro del rectángulo.
A) 9m
B) 8m
C) 10m
D) 11m
E) 12m
Rpta. : "B"
PREGUNTA 15 :
En una pirámide triangular ABCD de base BCD sean M y N baricentros de las caras BCD y ABC, AM y ND se intersectan en F. Si FM = 7m; calcular la longitud de AF (en M ).
A) 19
B) 17
C) 21
D) 18
E) 15
Rpta. : "C"
PREGUNTA 16 :
Un tronco de pirámide de bases paralelas tiene por base mayor un cuadrado de lado 2 unidades. Si la altura del tronco es de 3 unidades y su volumen es 7 unidades cúbicas. ¿Cuánto mide el lado de la base menor?.
A) 1/2
B) 3
C) 4
D) 3/2
E) 1
Rpta. : "E"
PREGUNTA 17 :
En un tronco de pirámide, se traza un plano secante y paralelo a las bases, que divide a la arista lateral en la razón de 2 a 3. Si la sección determinada está más próxima a la base menor y las áreas de las bases son iguales a 4 y 9, calcule el área de la sección determinada.
A) 144/25
B) 161/25
C) 144/17
D) 164/25
E) 256/25
Rpta. : "A"
PREGUNTA 18 :
Un tronco de pirámide pentagonal regular tiene de perímetros de sus bases 15 cm y 45 cm; y la arista lateral mide 5 cm. Halle el apotema del tronco (en cm).
A) 6
B) 3
C) 4
D) 2
E) 1
Rpta. : "C"
PREGUNTA 19 :
El volumen de un tronco de pirámide cuadrangular es 74m³ , si su altura mide 6m. y el área de una de las bases es 16m². ¿Cuál es el área de la otra base?.
A) 49m²
B) 25m²
C) 9m²
D) 16m²
E) 12m²
Rpta. : "C"
PREGUNTA 20 :
El área de la superficie lateral de una pirámide cuadrangular regular es 128 𝑐𝑚². Si el radio de la circunferencia circunscrita a la base es 2√2 𝑐𝑚, calcule el volumen de la pirámide:
A) 67√15/3 𝑐𝑚³
B) 32√7 𝑐𝑚³
C) 32√15 𝑐𝑚³
D) 65√15/3 𝑐𝑚³
E) 64√15/3 𝑐𝑚³
Rpta. : "E"
PREGUNTA 21 :
Desde un punto exterior a un plano se trazan tres oblicuas congruentes de 14 m de longitud, de modo que sus pies son los vértices de un triángulo equilátero cuya área es 81√3/4 m². Calcule la distancia del punto al plano.
A) 19
B) 17
C) 21
D) 18
E) 13
Rpta. : "E"
PREGUNTA 22 :
Calcule el volumen de una pirámide O-ABC, cuyas caras laterales determinan diedros de medida 45° con la base, si AB=13, BC=15 y AC=14 .
A) 100
B) 106
C) 108
D) 112
E) 115
Rpta. : "D"
PREGUNTA 23 :
Se tiene un prisma recto de base cuadrangular de volumen 𝕍 . Calcule el volumen del sólido, cuyos vértices son los puntos de intersección de las diagonales en todas las caras .
A) 𝕍/6
B) 𝕍/3
C) 𝕍/4
D) 𝕍/12
E) 𝕍/8
Rpta. : "A"
PREGUNTA 24 :
Se tiene una pirámide V - ABCD, tal que ABCD es un paralelogramo, cuyas diagonales miden AC= 10 y BD= 8.
Calcule el valor de (VA)² + (VC)² – (VB)² – (VD)²
A) 24
B) 20
C) 28
D) 18
Rpta. : "D"
PREGUNTA 25 :
Halle el volumen de una pirámide triangular regular cuya base está inscrita en una circunferencia de radio 2 y forma con las caras laterales diedros que miden 45°.
A) √3
B) 2√3
C) 3√3
D) √3/2
Rpta. : "A"
PREGUNTA 26 :
En una pirámide A - BCD, las caras ABC, ADC y ABD forman ángulos de igual medida con la base e iguales a 60°. Si el área de la base es 60 𝑢², calcule el área de la superficie lateral de la pirámide.
A) 150 𝑢²
B) 160 𝑢²
C) 170 𝑢²
D) 190 𝑢²
E) 120 𝑢²
Rpta. : "E"
PROBLEMAS RESUELTOS
PREGUNTA 1 :
En una pirámide cuadrangular regular el apotema de la base es 6 cm y el apotema del sólido es 10 cm. Calcula el volumen de la pirámide.
A) 250 cm³
B) 384 cm³
C) 275√3 cm³
D) 420 cm³
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 2 :
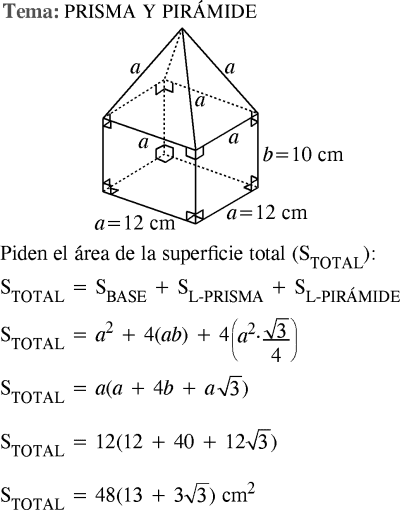
En una empresa se realizó un intercambio de regalos para fomentar el compañerismo entre sus trabajadores. Uno de esos regalos se representa en la figura, cuya base es un prisma cuadrangular regular, y la parte superior es una pirámide cuadrangular regular con caras laterales en forma de triángulos equiláteros. Calcule el área de la superficie de dicho regalo.
A) 42(15 + 3√3) cm²
B) 144(3 + √3) cm²
C) 24(11 + 3√3) cm²
D) 48(13 + 3√3) cm²
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 3 :
La base de una pirámide es un hexágono regular de √3 m de apotema. Si la altura es el doble del apotema de su base, entonces el volumen de dicho sólido, en m³, es
A) 8
B) 10
C) 12
D) 14
E) 16
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 4 :
Se tiene una pirámide regular V-ABCDEF, se ubica los puntos medios M,N y S en las aristas VA, VE y VD, luego se grafica el prisma triangular recto MNS-PQR tal que P, Q y R están en la base de la pirámide. El área de la superficie lateral y la altura del prisma es de 30√3 y 10 respectivamente. Calcule el volumen de la pirámide.
A) 10√3
B) 40
C) 20√3
D) 40√3
RESOLUCIÓN :
Rpta. : "D"