INDUCCIÓN Y DEDUCCIÓN EJERCICIOS RESUELTOS DE RAZONAMIENTO LÓGICO MATEMÁTICO PDF
PREGUNTA 1 :
En la siguiente secuencia de figuras formadas por cubos idénticos, ¿cuántas caras de los cubos están en contacto entre sí en la figura 40?
.png)
A) 80
B) 68
C) 160
D) 100
RESOLUCIÓN :
.png)
Rpta. : "C"
PREGUNTA 2:
En su preparación para ingresar a la universidad, José se propone resolver una cantidad de problemas cada semana, de acuerdo con la siguiente secuencia:
¿Cuántos problemas resolverá en la décima semana?
A) 124
B) 200
C) 100
D) 144
RESOLUCIÓN :
.png)
Rpta. : "D"
PREGUNTA 3 :
En la siguiente secuencia de figuras, calcule la suma de todos los elementos de la figura 11.
A) 2626
B) 2642
C) 2662
D) 2862
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 4 :
La municipalidad de Lima usó material reciclable para sus adornos navideños. En uno de sus adornos usó botellas idénticas: sobre la pared de un edificio, armaron un gran árbol navideño en forma triangular usando botellas de plástico en desuso, como se muestra en la figura. Si en la base hay 100 pares de botellas, ¿cuántas botellas en total se utilizaron para construir dicho árbol?
A) 10 000
B) 5050
C) 10100
D) 5500
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 5 :
Eduardo cada vez que llega su padrino se pone muy contento, pues siempre le dejan una buena propina, esta vez su padrino le dice: “si resuelves la siguiente operación sin calculadora, te daré de propina en soles, la suma de cifras del resultado”.
¿Cuánto recibirá de propina Eduardo?
.png)
A) S/ 179
B) S/ 253
C) S/ 549
D) S/ 457
RESOLUCIÓN :
.png)
Rpta. : "D"
PREGUNTA 6 :
¿Cuántas filas tendrá el arreglo triangular, formado por 120 monedas?
a) 14
b) 20
c) 16
d) 15
e) 18
RESOLUCIÓN :
.png)
Rpta. : "D"
PREGUNTA 7:
Las torres mostradas han sido construidas con piezas cúbicas idénticas a la que muestra la figura 1. Determine el número de cubos que tendrá la torre de la figura 10.
A) 2025
B) 2500
C) 3025
D) 2916
RESOLUCIÓN :
.png)
Rpta. : "C"
PREGUNTA 8 :
La municipalidad de cierto distrito necesita construir un conjunto de 38 estructuras metálicas, como las que muestra la secuencia de figuras adjunta. Luego de convocar a varios cerrajeros, optó por contratar a uno que cobrará por cada estructura metálica de acuerdo con el número máximo de triángulos que se pueda contar en dicha estructura. Si por cada triángulo que se pueda contar en la estructura cobra S/1,5, ¿cuánto cobrará por la estructura correspondiente a la figura 38?
A) S/ 2340
B) S /1170
C) S/1380
D) S/ 2370
RESOLUCIÓN :
.png)
Rpta. : "A"
PREGUNTA 9 :
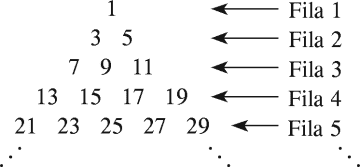
En la siguiente secuencia, halle la suma de todos los números ubicados en la fila 10.
A) 1 012
B) 1 009
C) 1 010
D) 1 010
E) 1 008
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 10 :
En la secuencia de figuras, determine el número de hexágonos de la figura 37.
.png)
A) 188
B) 192
C) 187
D) 177
RESOLUCIÓN :
.png)
Rpta. : "C"
PREGUNTA 11 :
En el siguiente arreglo numérico triangular, halle el primer término de la fila 21.
A) 144
B) 441
C) 421
D) 444
E) 134
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 12 :
En la figura mostrada se tienen 20 rombos y 3 rectas paralelas, ¿cuántos puntos de intersección existen en total?
.png)
A) 198
B) 156
C) 158
D) 202
RESOLUCIÓN :
El número de puntos de intersección es:
3(2×20) + 2×19 + 2×20 = 198
Rpta. : "A"
PREGUNTA 13 :
El arreglo numérico mostrado cuenta con 10 filas, calcule la suma del primer y último término de la fila 10.
.png)
A) 240
B) 238
C) 236
D) 210
RESOLUCIÓN :
.png)
Rpta. : "C"
Nunca olvides que el primer paso es comprender el problema, una vez logrado esto debes dar el siguiente paso: idear cómo afrontarlo; cada problema debe ser un reto, para ello debes leer atentamente la parte teórica y rescatar las mayores observaciones de cada ejemplo.
Después de haber resuelto un problema, debes valorar más el proceso inductivo-deductivo y no tanto la respuesta, ello te permitirá salir airoso en cada problema siguiente.
El objetivo entonces del presente capítulo será estudiar los diversos conceptos y aplicarlos manejando criterios adecuados, desarrollando, además, ejemplos necesarios para un mejor desenvolvimiento dentro del curso de razonamiento y actividades en general.
Quizá en algunas ocasiones, durante la búsqueda de la solución de alguna interrogante relacionada con nuestra vida diaria o al intentar resolver problemas netamente matemáticos, nos hayamos encontrado un tanto desorientados sobre cómo afrontarlos, entonces nos asaltó la duda y surgieron las eternas preguntas:
¿Por dónde empezar?
¿Qué estrategia plantear y seguir?
Parte de culpa de estar en dicha situación la tiene el hecho de no tener en claro los conceptos de razonamiento, pensamiento creativo, lógica deductiva, lógica inductiva, etc.
En consecuencia, nos corresponde revertir esta situación, poniendo en práctica nuestra capacidad de raciocinio y análisis objetivo.
Contribuiremos a ello, en esta parte del curso, desarrollando la parte inductiva deductiva de nuestro razonamiento para lograr, de esta manera, un mayor grado de abstracción.
Las expresiones: "soy incapaz para la matemática", "no he nacido para los números", "me falta memoria para aprender todas las fórmulas", etc., etc., son un producto amargo del tipo de enseñanza memorística y mecanizada que hemos recibido desde nuestra infancia, debido a la falta de un sistema educativo adecuado, objetivo y verdaderamente científico capaz de satisfacer las expectativas de la gran mayoría de estudiantes y no sólo de un sector, cuyo beneficio obedece claramente a intereses egoístas.