GEOMETRÍA EVALUACIÓN RESUELTA DE ADMISIÓN UNIVERSIDAD

PREGUNTA 81 :

En un prisma hexagonal regular, la arista lateral es el doble de su arista básica y el volumen del prisma es 24√3 u³. Calcule el área lateral del prisma.

A) 36 u²

B) 48 u²

C) 40 u²

D) 50 u²

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 82 :

En un cono de 8 cm de altura y de radio 5, calcule la generatriz del cilindro inscrito en el cono si el área lateral del cilindro es 20𝛑 u².

A) 2

B) 4

C) 6

D) 8

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 83 :

En un cubo de arena se hace una excavación de una esfera cuyo diámetro es igual a la arista del cubo y el radio de la esfera es 3 cm. Calcule el volumen restante de la arena.

A) 12(5 –𝛑) u³

B) 24(6 –𝛑) u³

C) 36(6 –𝛑) u³

D) 26(5 –𝛑) u³

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 84 :

En un triángulo rectángulo ABC se prolonga la hipotenusa hasta un punto D.

Si BC=CD=7 y AD=32, calcule la altura relativa a la hipotenusa.

A) 6,25

B) 6,72

C) 5,12

D) 5,25

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 85 :

En un paralelogramo de lados 6 y 16, la distancia entre los lados menores es 8. Calcule la distancia entre los lados mayores.

A) 1

B) 3

C) 5

D) 4

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 86 :

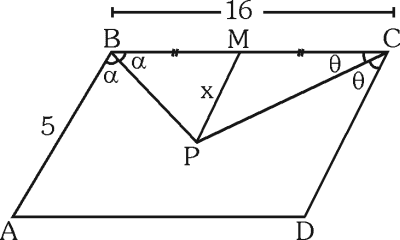
En un paralelogramo ABCD, AB=5 y BC=16. Si P es el punto de intersección de las bisectrices interiores de los ángulos B y C, calcule la distancia del punto P al punto medio del lado BC.

A) 2

B) 4

C) 6

D) 8

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 87 :

En un triángulo de lados 6 y 12 se inscribe un rombo, calcule el lado de dicho rombo.

A) 1

B) 2

C) 3

D) 4

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 88 :

En un triángulo rectángulo, la longitud de uno de sus catetos es BC=√2. Si el otro cateto tiene por longitud la tercera parte de la hipotenusa, calcule la longitud de la hipotenusa.

A) 0,5

B) 1

C) 1,5

D) 2

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 89 :

Del gráfico, calcule el área sombreada, si PQ=2, R=√2 (T: punto de tangencia).

A) 2√2 – 2 – 𝛑/2

B) 2√2 – 1 – 𝛑/2

C) 2√2 + 1 – 𝛑/2

D) 2√2 – 1 – 𝛑/2

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 90 :

Se tienen los segmentos colineales y consecutivos AM y MB, tal que el segmento MN es perpendicular a AB, tal que NB=AB=5 y MN=2(AM). Calcule el área de la región triangular MNB.

A) 4 u²

B) 5 u²

C) 6 u²

D) 8 u²

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 91 :

En el gráfico, AB=BL=LP=PC y AD=DL=LQ=QC. Calcule: x+y

A) 50º

B) 30º

C) 40º

D) 60º

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 92 :

En un cuadrado ABCD, se construye internamente el triángulo equilátero APD. Calcule la medida del ángulo determinado por los segmentos BD y AP.

A) 50º

B) 90º

C) 75º

D) 80º

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 93 :

Se tienen dos triángulos equiláteros, uno inscrito y el otro circunscrito a una misma circunferencia. Si el área de la región determinada por las dos regiones triangulares es 9√3 u², calcule la longitud de la circunferencia.

A) 3𝛑

B) 2𝛑

C) 4𝛑

D) 6𝛑

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 94 :

Se tienen, sobre una recta, los puntos consecutivos A, B, C y D, tal que

BC=5 y 7AD – BC=2AC+7BD.

Calcule AB.

A) 2

B) 3

C) 4

D) 1

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 95 :

Se tienen dos circunferencias circunscritas a dos hexágonos regulares. Si sus radios miden 4 y 8, calcule la relación de áreas de las regiones determinadas entre las circunferencias y sus polígonos regulares inscritos.

A) 1/4

B) 1/2

C) 1/8

D) 1/6

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 96 :

Se tiene un globo inflado con helio atado con una cuerda al piso de un campo. Si un viento empuja al globo 30 m horizontalmente y si la cuerda que lo sostiene mide 50 m, calcule a qué altura del piso queda el globo.

A) 30

B) 40

C) 50

D) 45

RESOLUCIÓN :