FACTORIZACIÓN POR ARTIFICIOS SUMAS RESTAS QUITA Y PON CAMBIO DE VARIABLE EJEMPLOS EJERCICIOS RESUELTOS PDF
ARTIFICIOS DIVERSOS
Para facilitar la factorización se puede hacer uso de los siguientes artificios:
POR CAMBIO DE VARIABLE
Cuando se repite una misma expresión en el polinomio, se usa el cambio de variable.
EJEMPLO 1 :
Factorice el polinomio
V(x)=(x² + x + 2)² – 5 (x²+x+2)+6
RESOLUCIÓN :
Haciendo el cambio de variable:
x²+ x + 2 = a
Con lo cual, el polinomio quedará así:
a² – 5a + 6 = (a – 3)(a – 2)
Como a = x² + x + 2
Entonces reponiendo:
V(x) = (x²+ x + 2 – 3) (x²+ x + 2 – 2)
Luego:
V(x)=(x²+x–1)(x²+x)=x(x+1)(x²+x –1)
EJEMPLO 2 :
Factorice el polinomio:
A(x)=(x²+ 3x+1)² – 6(x²+3x+1)+5
RESOLUCIÓN :
Haciendo cambio de variable:
a = x²+ 3x + 1, entonces:
A = a² – 6a + 5 = (a – 1)(a – 5)
Luego, restituyendo:
A(x)=(x²+ 3x+1 – 1)(x²+3x+1– 5)
= (x²+ 3x)(x²+ 3x – 4)
A(x)=x(x+3)(x+4)(x – 1)
POR AGRUPACIÓN ADECUADA
Aplicando la propiedad asociativa de la multiplicación y en forma adecuada para luego hacer un cambio de variable, se simplifica el proceso operativo.
EJEMPLO 3 :
Factorice:
B(x)=(x+2)(x+3)(x+5)(x+6) – 40
RESOLUCIÓN :
Agrupemos los factores de 2 en 2 tal que resulta una expresión repetida; para ello la suma de términos independientes en cada grupo debe ser una misma cantidad.
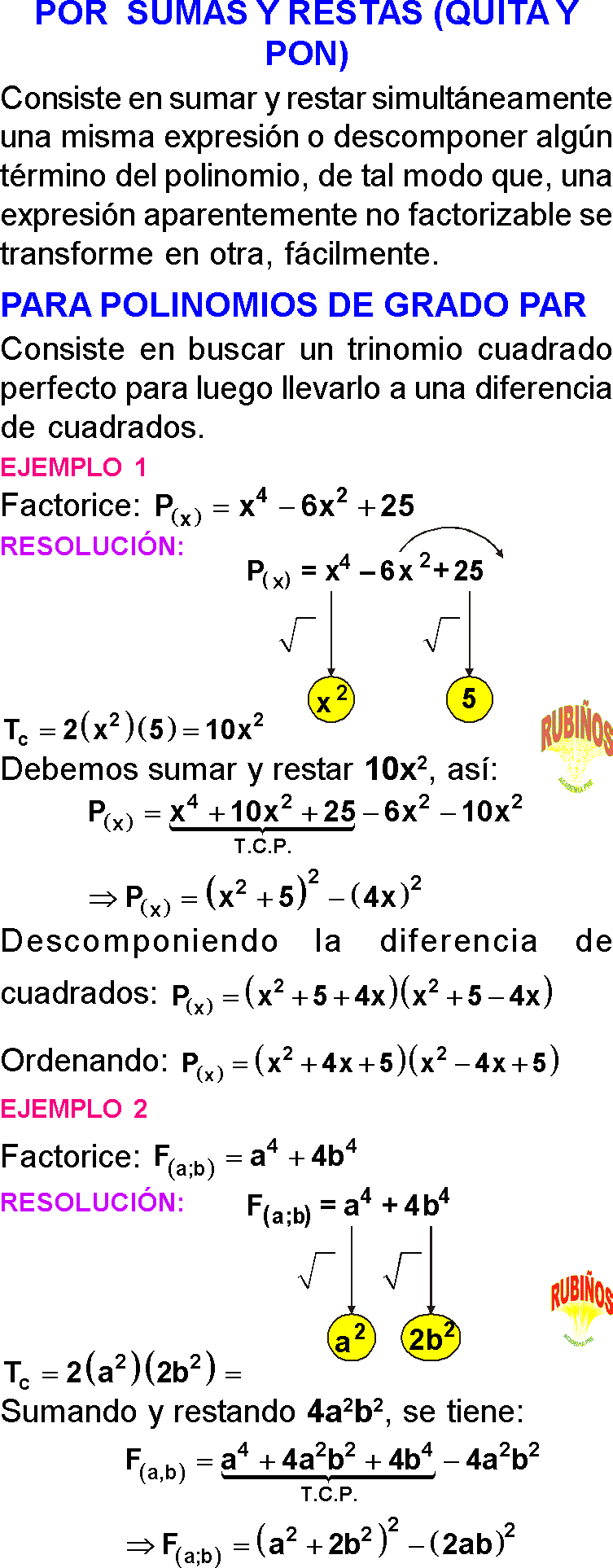
POR MÉTODO DE SUMAS Y RESTAS (Y OTROS ARTIFICIOS)
Se inspecciona el dato, comparándolo con alguna identidad conocida, la mayoría de veces será necesario aumentar algunos términos para construir en forma completa aquella identidad sugerida por el dato, naturalmente que aquellos términos agregados deben ser quitados también para así no alterar el origen .
Este método conduce la mayoría de las veces a una diferencia de cuadrados , suma de cubos o diferencia de cubos.
EJEMPLO 4 :
Factorizar:
x⁴ + 64y⁴
RESOLUCIÓN :
Sumando y restando:
16x²y²x⁴ + 64y⁴ + 16x²y²– 16x²y²x⁴+ 16x²y²+ 6⁴y⁴ –16x²y²(x²+ 8y²)²– (4xy)² de donde:
(x²+ 8y²+ 4xy)(x²+ 8y²– 4xy)
EJEMPLO 5 :
Factorizar: P(x) = x⁴+ 4a⁴
RESOLUCIÓN :
=(x²)²+(2a²)²+2(x²)(2a²)–2(x²)(2a²)
= (x²+ 2a²)² – (2ax)²
= (x²+ 2a²+ 2ax)(x²+ 2a²– 2ax)
EJEMPLO 6 :
Factorizar:
(a+b+c–2)²+(a+b+c–1)²–5(a+b+c+1)²
RESOLUCIÓN :
Si dos o más términos se repiten constantemente, se sugiere hacer cambio de variable.
Haciendo: x = a + b + c
Entonces al reemplazar resulta:
(x – 2)² +(x –1)² – 5(x + 1)
= x²– 4x +4+x²– 2x+1– 5x – 5
=2x²–11x=x(2x–11)
Pero como: x=a+b+c
Entonces la factorización pedida será:
(a+b+c)[2(a+b+c) – 11 ]
EJEMPLO 7 :
Factorice:
E(x) = x⁵+ x + 1
RESOLUCIÓN :
Cuando el polinomio es de grado impar, se busca generalmente una suma o diferencia de cubos. En nuestro caso le sumamos y restamos x²
E(x) = x⁵ – x² + x² + x + 1, agrupando
E(x)= (x⁵– x²) + (x²+ x + 1)
E(x)= x²(x³ – 1) + (x²+ x + 1)
E(x)= x²(x –1)(x²+x+1) + (x²+ x +1)
E(x)=(x³ – x²)(x²+ x + 1) + (x²+ x +1)
E(x)= (x²+x+1) (x³ – x²+ 1)