DIFERENCIA DE CONJUNTOS EJEMPLOS Y EJERCICIOS RESUELTOS PDF
CONJUNTO DIFERENCIA
La diferencia de dos conjuntos (A – B) es la operación que nos permite obtener un nuevo conjunto que agrupe a todos los elementos de A que no pertenecen a B.
El conjunto diferencia (A–B) en ese orden es aquel que está formando únicamente por los elementos exclusivos de A, es decir no deben pertenecer a B.
Dados dos conjuntos A y B, el conjunto diferencia entre A y B es el conjunto formado por todos los elementos de A que no pertenecen a B.
Al conjunto diferencia entre A y B se le representa por A – B, y se lee «diferencia de A y B».
EJEMPLO 1 :
Sean los conjuntos:
A= {1; 2; 3; 4; 5}
B= {3; 4; 6}
A – B es otro conjunto cuyos elementos pertenecen al conjunto A pero no al conjunto B, es decir: {1; 2; 5}
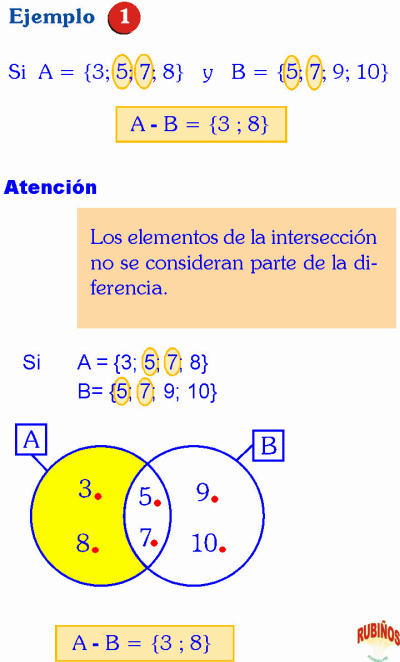
Los elementos de la intersección no se consideran parte de la diferencia.
EJEMPLO 2 :
Sean los conjuntos:
P={a, b, c, d, e}
Q = {b, c, d}
Calcular: P – Q
RESOLUCIÓN :
Como se podrá observar, el conjunto "Q" está contenido en el conjunto "P" es decir, Q⊂P.
Entonces, existen elementos que pertenecen al conjunto P pero no al conjunto Q.
Entonces: P – Q = {a; e}
EJEMPLO 3 :
Sean los conjuntos:
M={2; 4; 6}
N = {1; 3}
Calcular M – N
RESOLUCIÓN :
Como se podrá observar, los dos conjuntos son disjuntos (no tienen elementos comunes). En este caso, la diferencia es: {2; 4; 6}
EJEMPLO 4 :
Sean los conjuntos:
A = {2; 4; 6; 8)
B = {4; 6; 9}
Calcular A – B y B – A
RESOLUCIÓN :
Calculamos A – B = {2; 8}
Calculamos B – A = {9}
Observa que A–B, es diferente que B–A, entonces: A – B≠B – A
EJERCICIO 1 :
Dados los conjuntos:
A = {1; 2; 3; 5}
B = {2; 4; 5; 6; 7}
Hallar: A – B
RESOLUCIÓN :
Como se observará los elementos comunes para ambos conjuntos son: 2 y 5, luego la diferencia A – B es lo que sobra del conjunto A, o sea: A – B = {1; 3}
Y la diferencia B – A es lo que sobra del conjunto B, o sea: B – A= {4; 6; 7}
EJERCICIO 2 :
Dados los conjuntos:
A = {2; 4; 6}
B = {3;5}
Hallar: A – B
RESOLUCIÓN :
Como se observa los dos conjuntos son disjuntos, o sea, no hay ningún elemento en común. Luego:
A – B= A ⇒ A – B= {2; 4; 6}
EJERCICIO 3 :
Sean los conjuntos
A = {1; 2; 3; 4; 5; 6}
B = {2; 3; 5}
Hallar: A – B
RESOLUCIÓN :
A – B= {1;4;6}
Son elementos que sobran de A
Pero: B – A=Ø={ }; no sobra ningún elemento en B
EJERCICIO 4 :
Sean los conjuntos
A={x∈ℕ/3≤x<9}
B={x∈ℕ/2< x≤8}
Hallar: A – B
RESOLUCIÓN :
De la expresión: 3≤x<9; los valores que toma “x” son:
3; 4; 5; 6; 7 y 8. ⇒ A = {3; 4; 5; 6; 7; 8}
De la expresión: 2< x≤8; los valores que toma “x” son:
3; 4; 5; 6; 7 y 8. ⇒ B ={3; 4; 5; 6; 7; 8}
Luego: A – B =Ø={ }
EJERCICIO 5 :
Dados los conjuntos:
A = {1; 2; 3; 4; 5}
B= {3; 4; 5}
C = {2; 3}
Calcular:
a) A – B =
b) A – C =
c) B – C =
EJERCICIO 6 :
Dados los conjuntos:
P = {a, b, c, d}
Q = {b, c, d, e}
R = {a, b, c, d, f}
Calcular:
a) Q – P =
b) Q – R =
c) P – R =





















.gif)
.gif)
.gif)
.gif)

