ÁNGULOS DIEDROS Y TRIEDROS EJERCICIOS RESUELTOS PDF
APRENDIZAJES ESPERADOS
• Conocer la definición de ángulo diedro
• Aplicar adecuadamente el concepto de planos perpendiculares.
• Entender como calcular la distancia entre dos rectas alabeadas.
• Aplicar lo aprendido en la resolución de problemas.
• Conocer la definición de ángulo triedro y su clasificación.
• Reconocer a los diedros que se construyen en esta figura geométrica.
• Aplicar adecuadamente los teoremas relacionados al triedro en los problemas.
En nuestro día a día siempre nos vamos a encontrar con situaciones que nos dan la idea de planos, por ejemplo una laptop, el techo de algunas casas, etc. En estos casos la disposición de los planos nos pueden representar la idea de una nueva figura geométrica.
También podemos tener en cuenta que, cuando se realiza alguna construcción, se debe tener en cuenta las especificaciones del plano, ya que en ella encontraremos la información necesaria para realizar dicha edificación de la manera precisa y segura, por ejemplo las distintas distancias entre ciertas vigas y/o columnas.
ÁNGULO DIEDRO :
Es la figura geométrica formada por la unión de dos semiplanos que tienen en común su recta de origen a la cual se le denomina arista del ángulo diedro (Los semiplanos deben estar en distintos planos).
MEDIDA DEL ÁNGULO DIEDRO:
por un punto de la arista del diedro se trazan dos rectas perpendiculares a la arista, cada una de las perpendiculares se encuentran en cada una de las caras.
PLANOS PERPENDICULARES :
Dos planos son perpendiculares, cuando determinan un diedro que mide 90°.
PLANO BISECTOR DE UN ÁNGULO DIEDRO :
Es aquel plano que contiene a la arista del ángulo diedro y que determina con las caras otros dos ángulos diedros de igual medida.
Todo punto del plano bisector está a igual distancia de las caras de dicho ángulo diedro.
DIEDROS CONGRUENTES:
dos diedros son congruentes cuando tienen igual medida. Clasificación de los ángulos diedros :
Según su medida los ángulos diedros se clasifican en:
DIEDRO AGUDO:
si su ángulo plano es agudo.
DIEDRO RECTO:
si su ángulo plano es recto.
DIEDRO OBTUSO:
si su ángulo plano es obtuso.
DIEDRO LLANO:
si su ángulo plano es llano. Como en la Geometría Plana, según su posición, los diedros también pueden ser: consecutivos, adyacentes y opuestos por la arista.
También hay diedros complementarios (si sus ángulos planos suman 90°) y diedros suplementarios (si sus ángulos planos suman 180°).
ÁREA DE PROYECCIÓN ORTOGONAL DE UNA FIGURA PLANA SOBRE UN PLANO DADO :
El área de la proyección ortogonal de una región plana sobre un plano dado, es igual al producto del área de dicha región con el coseno del ángulo diedro determinado por el plano de la región y el plano dado.
ÁNGULO POLIEDRO
El ángulo poliedro, ángulo sólido o anguloide, es la porción de espacio que se encuentra delimitado por tres o más ángulos planos no coplanarios que tienen el vértice común.
ELEMENTOS :
VÉRTICE:
es el vértice común de los ángulos planos.
CARAS: son los ángulos planos.
ARISTAS: son los lados de los ángulos planos, cada arista pertenece a dos caras.
DIEDROS:
son los ángulos diedros que forman los planos de dos caras contiguas.
ÁNGULO TRIEDRO
El triedro es un ángulo poliedro de tres caras. Es decir es aquel ángulo sólido que se determina por tres rayos concurrentes entre sí dos a dos.
PROPIEDADES DE UN ÁNGULO TRIEDRO :
I) En todo ángulo triedro la suma de los valores de sus caras es mayor que 0° pero menor que 360°.
0° < a + b + c < 360°
II) En todo ángulo triedro el valor de una cara es menor que la suma de las otras dos pero mayor que la diferencia de ellas mismas.
b – c < a < b + c
a – c < b < a + c
a – b < c < a + b
III) En todo ángulo triedro la suma de sus ángulos diedros es mayor que 180° pero menor que 540°.
IV) En todo triedro la suma de los dos diedros es menor al tercero aumentando en 180º
TEOREMA :
En todo ángulo poliedro la suma de las caras es menor que 360º y mayor que 0º.
CLASES DE ÁNGULOS TRIEDROS
I) UNIRECTÁNGULO: Una cara mide 90°.
II) BIRECTÁNGULO: Dos caras miden 90°.
III) TRIRECTÁNGULO:
Las tres caras miden 90°.
IV) ISÓSCELES:
Dos caras son de igual medida.
V) EQUILÁTERO:
Las tres caras son de igual medida.
En todo triedro a dos diedros desiguales se oponen caras desiguales, y a mayor diedro se opone mayor cara.
Si un triedro tiene dos caras iguales los diedros opuestos son también iguales.
En todo triedro isósceles, el plano bisector del diedro comprendido entre las caras iguales, es perpendicular a la tercera cara, y determina dos ángulos iguales.
Toma en cuenta :
Los ángulos triedros se clasifican según los siguientes criterios:
I) Por la comparación de las medidas de sus caras :
TRIEDRO ESCALENO :
Es aquel que tiene sus tres caras de diferentes medidas.
TRIEDRO ISÓSCELES :
Es aquel que tiene dos caras de igual medida a los cuales se oponen diedros congruentes.
CONGRUENCIA DE TRIEDROS
En los triedros pueden demostrarse estos cuatro criterios de congruencia , los tres primeros se corresponden con los tres de los triángulos
PRIMER CRITERIO DE CONGRUENCIA :
Dos triedros que tengan iguales una cara e igual diedros adyacentes a dicha cara serán congruentes.
SEGUNDO CRITERIO DE CONGRUENCIA :
Dos triedros que tengan respectivamente iguales 2 caras e igual el diedro comprendidas por dichas caras serán congruentes.
TRIEDRO EQUILÁTERO :
Es aquel que tiene sus tres caras de igual medida y sus tres ángulos diedros congruentes.
II) POR EL NÚMERO DE CARAS RECTAS (DE MEDIDA IGUAL A 90°) :
TRIEDRO RECTÁNGULO
Es aquel que tiene una cara que mide 90°.
TRIEDRO BI-RECTÁNGULO
Es aquel que tiene dos caras que miden 90°.
A los cuales se oponen diedros que miden 90°.
TRIRECTÁNGULO
Es aquel que tiene sus tres caras que miden 90°, entonces sus tres diedros miden 90°.
TERCER CRITERIO DE CONGRUENCIA :
Dos triedros son congruentes si tiene sus tres caras iguales.
CUARTO CRITERIO DE CONGRUENCIA :
Dos triedros son congruentes cuando tienen iguales los tres diedros.
TRIEDRO POLAR O TRIEDRO SUPLEMENTARIO
Se llama triedro polar o suplementario de un triedro dado aquel cuyas aristas son perpendiculares a las caras del otro.
TEOREMA:
Cuando dos triedros son suplementarios o polares se cumple que las caras de uno de ellos son los suplementos de los diedros del
GUIA DE CLASE
PREGUNTA 1 :
Dos caras de un ángulo triedro miden 100° y 160°. La tercera cara puede medir:
a) 80°
b) 110°
c) 60°
d) 40°
e) 20°
PREGUNTA 2 :
En el interior de un ángulo diedro se ubica un punto “P” que dista 6 y 5 cm de las caras y 10 cm de la arista. Calcular la medida de dicho ángulo diedro.
a) 45°
b) 60°
c) 67°
d) 53°
e) 97°
PREGUNTA 3 :
Un triángulo al ser proyectado sobre un plano determina un triángulo cuya área es la mitad del área del primero. El diedro que forman los planos de los dos triángulos mide:
a) 15°
b) 45°
c) 30°
d) 60°
e) 75°
PREGUNTA 4 :
Dos caras de un triedro miden 120° y 130° respectivamente, la tercera cara puede medir:
a) 10°
b) 20°
c) 110°
d) 120°
e) 130°
PREGUNTA 5 :
En un diedro AB que mide 30° se traza una esfera tangente a las caras del diedro en "P" y "Q". Hallar "PQ", si la distancia del centro de la esfera a AB es 12.
a) 3
b) 4
c) 6
d) 8
e) 9
PREGUNTA 6 :
Se tiene un triángulo rectángulo ABC: AB = 12; BC = 16. Por el vértice “B” se levanta la perpendicular BF al plano de ABC. Si: BF = 9,6. Hallar la medida del ángulo diedro que forman ABC y AFC.
a) 30°
b) 60°
c) 37°
d) 53°
e) 45°
PREGUNTA 7 :
¿Cuál es el máximo valor entero que puede asumir una cara de un triángulo equilátero?
a) 90°
b) 105°
c) 120°
d) 135°
e) 119°
PREGUNTA 8 :
Dos caras de un triedro miden 115° y 125°. Determinar entre qué valores puede variar la tercera cara.
a) 30° y 150°
b) 40° y 150°
c) 60° y 200°
d) 50° y 200°
e) 10° y 120°
PREGUNTA 9 :
En el triángulo rectángulo ABC los catetos AB y BC miden 15 y 20m respectivamente. Por “B” se levanta BP perpendicular al plano del triángulo, luego se une “P” con “A” y “C”. Calcular la medida del diedro AC, si: BP = 16 m.
a) 53°
b) 30°
c) 60°
d) 37°
e) 45°
PREGUNTA 10 :
Dos caras de un triedro miden 45° y el diedro comprendido mide 90°. Determinar el valor de la tercera cara.
a) 30°
b) 45°
c) 60°
d) 90°
e) 120°
PREGUNTA 11 :
Un ángulo diedro es de 114°. Calcular la medida del ángulo formado por las semirectas perpendiculares a sus caras trazadas desde un punto cualquiera del plano bisector del diedro.
a) 114°
b) 46°
c) 66°
d) 60°
e) 90°
PREGUNTA 12 :
Sea ABC un triángulo equilátero de 18 u de lado cuyo ortocentro es “M”. Si en “M” se levanta una perpendicular MD=√27 u al plano que contiene al triángulo. Hallar el ángulo diedro formado por el triángulo ADC y ABC.
a) 60°
b) 75°
c) 90°
d) 45°
e) 30°
PREGUNTA 13 :
Si en un triángulo rectángulo ABC recto en B, trazamos perpendicular al plano del triángulo donde BP=3,6 m, BC=12 my AB=9 m , hallar la medida del diedro P–AC–B.
A) 37º
B) 37°/2
C) 53°/2
D) 45°/2
E) 53º
PREGUNTA 14 :
En un triángulo ABC , recto en B, AB = 6 y BC=8. Por el vértice B se traza BF perpendicular al plano ABC tal que BF=4,8. Calcular la medida del ángulo que forman los planos ABC y AFC.
A) 30º
B) 37º
C) 45º
D) 53º
E) 60º
PREGUNTA 15 :
Se tiene un triángulo rectángulo ABC, recto en B, tal que AB = 8 y BC = 6. Si la distancia de al plano P que pasa por AC mide 2,4. Calcular la medida del diedro que forma el plano P con el plano del triángulo ABC.
A) 15º
B) 30º
C) 37º
D) 53º
E) 45º
PREGUNTA 16 :
Dado un ángulo diedro, tal que las distancias de un punto exterior a las caras de la arista miden:10√2 ; 12 y 20u respectivamente. Hallar la medida del ángulo diedro.
a) 72°
b) 68°
c) 98°
d) 82°
e) 60°
PROBLEMAS PROPUESTOS
PREGUNTA 1 :
Dos caras de un triedro miden 80° y 118° respectivamente. Halle los valores enteros , mínimo y máximo de la medida de la tercera cara.
A) 40°, 161°
B) 60°, 161°
C)30°, 161°
D) 28°, 161°
E) 39°, 161°
Rpta. : "E"
PREGUNTA 2 :
En un ángulo diedro, las distancias de un punto interior a las caras y a la arista miden 4√2 u, 4 u y 8 u respectivamente. Calcule la medida del ángulo diedro.
A) 65º
B) 70º
C) 75º
D) 80º
E) 85º
Rpta. : "C"
PREGUNTA 3 :
En un triángulo ABC , recto en B, los lados miden AB=6 y BC = 8 . Por el vértice de B se traza BF perpendicular al plano ABC tal que BF = 4,8.
Hallar la medida del ángulo diedro que forman los planos ABC y AFC .
A) 15°
B) 30°
C) 45°
D) 75°
E) 90°
Rpta. : "C"
PREGUNTA 4 :
El área proyectada de un cuadrado sobre un plano que pasa por una de sus diagonales es de 18,6 𝑐𝑚², si el ángulo formado por dichas superficies es de 53°.
Halle el área (en 𝑐𝑚²) del cuadrado.
A) 30,0
B) 30,5
C) 30,75
D) 31
E) 31,5
Rpta. : "A"
PREGUNTA 5 :
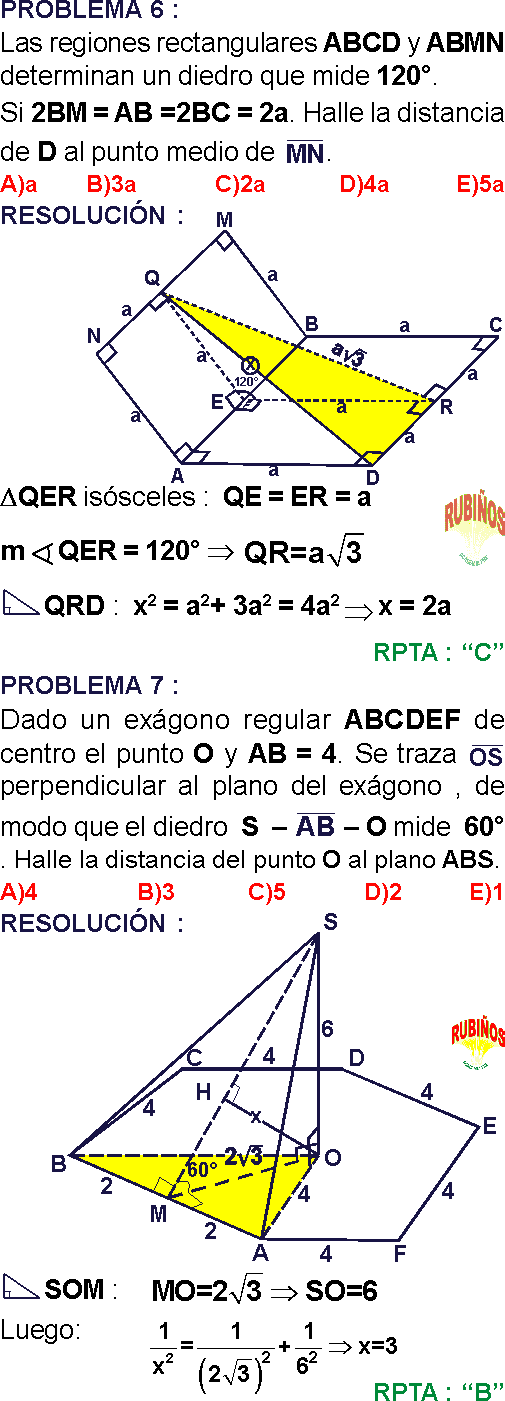
Las regiones rectangulares ABCD y ABMN determinan un diedro que mide 120°.
Si 2BM = AB =2BC = 2a. Halle la distancia de D al punto medio de MN .
A) a
B) 3a
C) 2a
D) 4a
E) 5a
Rpta. : "C"
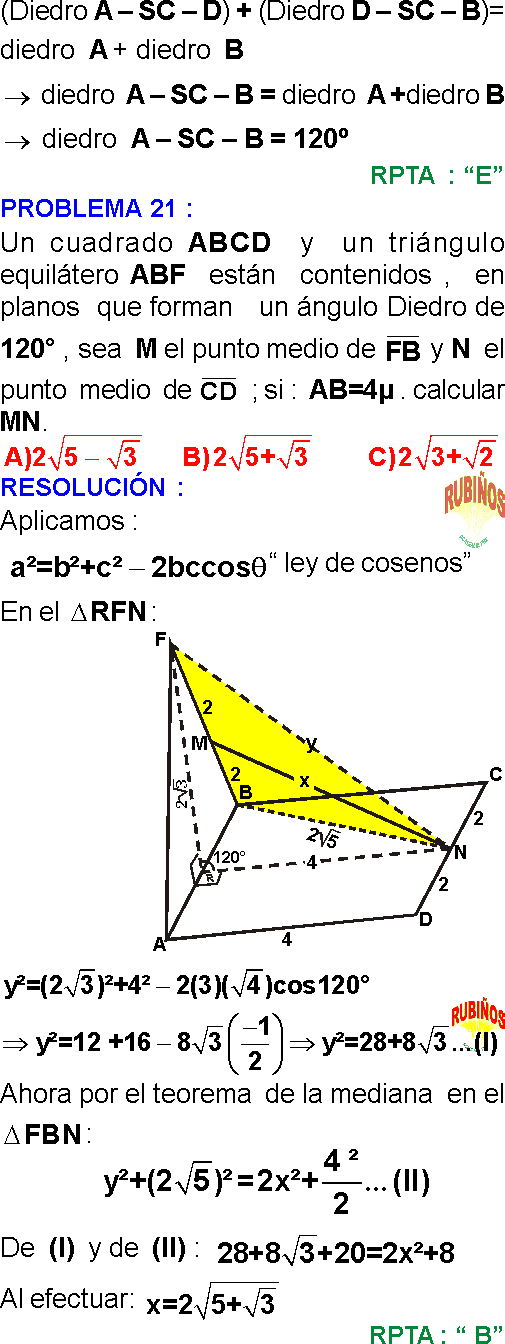
PREGUNTA 6 :
Dado un exágono regular ABCDEF de centro el punto O y AB = 4. Se traza perpendicular al plano del exágono , de modo que el diedro S–AB–O mide 60° . Halle la distancia del punto O al plano ABS.
A) 4
B) 3
C) 5
D) 2
E) 1
Rpta. : "B"
PREGUNTA 7 :
En un tetraedro O – ABC,OA=BC,OB=AC y OC= AB. Además se cumple AC >OC>AO. Halle la suma del máximo y mínimo entero de la cara AOC.
A) 90°
B) 100°
C) 120°
D) 150°
E) 160°
Rpta. : "D"
PREGUNTA 8 :
Dos regiones cuadradas están contenidos en plano perpendiculares ; ABCD y ABEF. Halle la medida del ángulo que determinan las rectas AC y BF .
A) 45°
B) 150°
C) 90°
D) 120°
E) 135°
Rpta. : "D"
PREGUNTA 9 :
Se tiene un triángulo ABC recto en B, contenido en un plano P, se ubica E un punto exterior a dicho plano tal que EA = EB = EC, si la distancia de E al plano P es 49 y AB = 14. Halle la medida del ángulo diedro (BC).
A) Arc tg 45
B) Arc tg 7
C) Arc tg 10
D) Arc tg 11
E) Arc tg 13
Rpta. : "B"
PREGUNTA 10 :
De las siguientes proposiciones.
I) En todo triedro convexo , un diedro exterior es menor que la suma de los otro dos y mayor que su diferencia.
II) La distancia de dos rectas que se cruzan en el espacio es el segmento perpendicular a ambas y cuyos extremos se encuentran uno en cada recta .
III) La proyección de toda poligonal sobre un plano es otra poligonal .
Son verdaderas :
A) Todas
B) Sólo II
C) I y III
D) I y II
E) II y III
Rpta. : "B"
PREGUNTA 11 :
Indicar la verdad de las siguientes proposiciones :
A) En todo triedro a caras congruentes se oponen diedros congruentes.
B) En todo triedro la suma de las medidas de los ángulos de sus caras está entre 180° y 540°
C) Triedro equilátero es aquel cuya medida de los ángulos de sus caras miden 60° cada uno
A) VVF
B) VFF
C) FFF
D) FFV
E) FVV
Rpta. : "B"
PROBLEMA 1 :
En la pirámide P–ABC, de altura PA , M es punto medio de PC y AM=BC.
Si m∢ABC=90°, calcula el orden de las medidas de los ángulos CPB , PCB y PBC.
A) 45°, 45°, 90°
B) 30°, 75°, 75°
C) 30°, 60°, 90°
D) 60°, 60°, 60°
RESOLUCIÓN :
Rpta. : "C"
PROBLEMA 2 :
Del vértice A del cuadrado ABG D se traza AP perpendicular al plano que contiene al cuadrado mencionado. Luego, se une el punto P con- los puntos medios M y N de BC y CD respectivamente. Si AP=18cm y AB=12√2cm, en el tetraedro A-PMN calcule la medida del ángulo diedro P-MN-A.