CARDINAL DE UN CONJUNTO EJEMPLOS Y EJERCICIOS RESUELTOS PDF
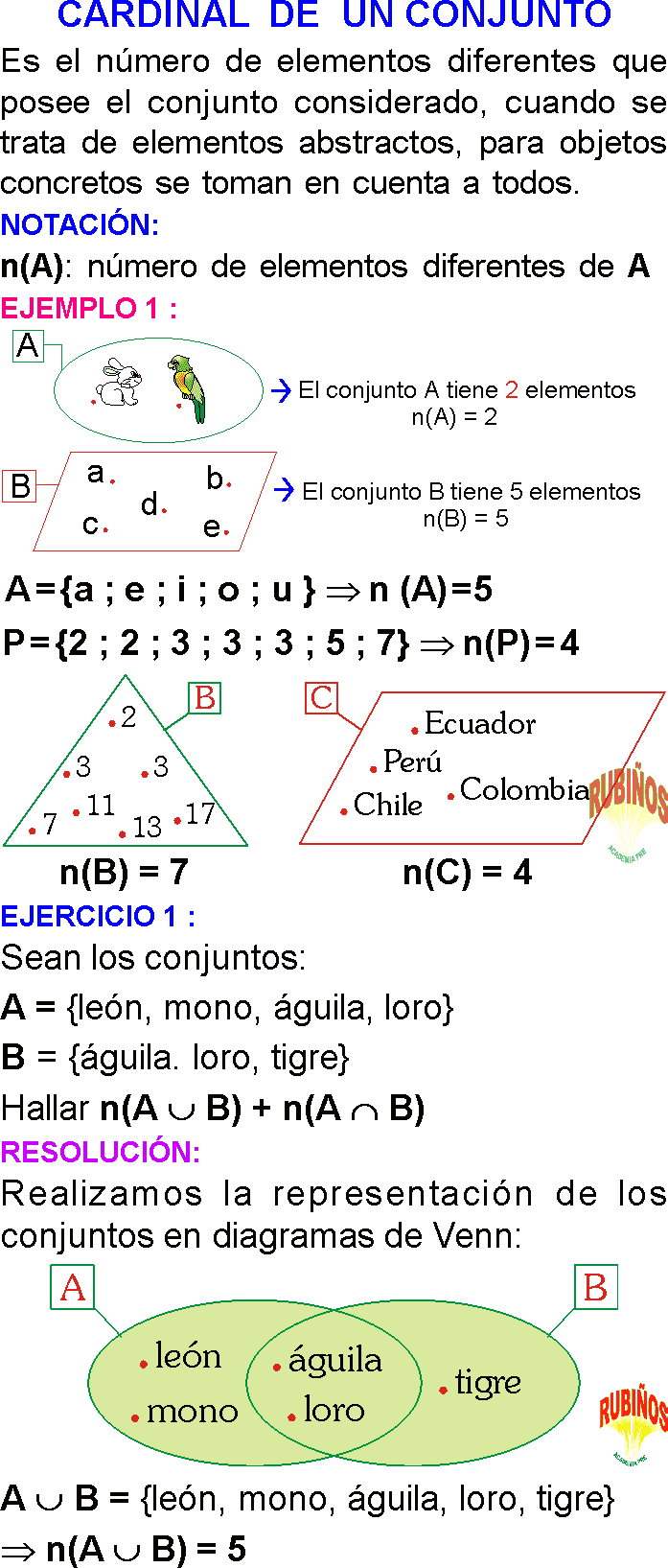
El cardinal de un conjunto es el número de elementos diferentes que posee el conjunto considerado, cuando se trata de elementos abstractos, para objetos concretos se toman en cuenta a todos.
NOTACIÓN:
n(A) : número de elementos diferentes de A
PROPIEDADES DEL NÚMERO DE ELEMENTOS DE UN CONJUNTO
EJERCICIO 1 :
Sean los conjuntos:
A = {león, mono, águila, loro}
B = {águila. loro, tigre}
Hallar n(A∪B) + n(A∩B)
EJERCICIO 2 :
Sean los conjuntos:
P = {1; 4; 5; 6}
Q = {2; 3; 5; 6; 7}
Hallar n(P – Q) + n(Q – P)
EJERCICIO 3 :
Si: n(A)=8 ; n(B)=10 y n(A∪B)=16
Halle: n(A∩B)
EJERCICIO 4 :
Dados los conjuntos:
A = {números naturales menores que 6}
B = {números naturales mayores que 3 y menores que 8}
Hallar n(A) + n(B)
EJERCICIO 5 :
Dados los conjuntos:
P = {letras de la palabra pluma}
Q = {letras de la palabra maíz}
Hallar n(P) + n(Q)
PRACTICA PROPUESTA
PREGUNTA 1 :
Halle el cardinal del conjunto
A={3x+ 2/ 2 < x < 10; x∈ℤ}
A) 5
B) 6
C) 7
D) 8
Rpta. : "C"
PREGUNTA 2 :
Si B = {(x + 1) / x∈ℕ ∧ 3x< x + 14}
Dar como respuesta el cardinal de B
A) 4
B) 5
C) 6
D) 7
E) 8
Rpta. : "D"
PREGUNTA 3 :
Si A = {(x² + 4) / x∈ℤ ∧ –4 < x < 6}
Hallar n(A)
A) 4
B) 5
C) 6
D) 7
E) 8
Rpta. : "C"
PREGUNTA 4 :
Halle el cardinal del conjunto
A= {(3x+ 2)∈ℤ/ 2 < x < 10}
A) 7
B) 14
C) 22
D) 23
Rpta. : "D"
PREGUNTA 5 :
Indique cuánto suman los elementos comunes de R y S.
R = {(x²+1) /x∈ℤ; 0 < x < 6}
S = {(x²+1)∈ℤ / 0 < x < 6}
A) 50
B) 60
C) 62
D) 42
Rpta. : "B"
PREGUNTA 6 :
Si el conjunto P={x – 3/9 ≤ x < 19; x∈ℤ}, ¿cuál de las siguientes proposiciones es correcta?
A) 17 pertenece al conjunto P.
B) 8 no pertenece al conjunto P.
C) El cardinal del conjunto P es 13.
D) Un elemento del conjunto P es 14.
Rpta. : "D"