ÁREAS DE REGIONES CUADRANGULARES EJERCICIOS RESUELTOS PDF
APRENDIZAJES ESPERADOS
• Conocer las fórmulas para calcular las áreas de regiones cuadrangulares.
• Identificar los nombres de las áreas de las regiones cuadrangulares , de acuerdo a la clasificación de los cuadriláteros.
• Aplicar lo aprendido en la resolución de problemas sobre regiones cuadrangulares.
A lo largo de la historia de la humanidad el hombre siempre ha tenido la necesidad de obtener las medidas de los terrenos, ya sea por el reparto de tierras o por el conocimiento de la extensión de la propiedad de la cual era propietario.
Esta necesidad lo llevó a realizar cálculos para obtener las medidas de las más variadas formas, de allí que esto a quedado catalogado en los libros de agrimensura a modo de tablas gráficas que permiten obtener el área de diferentes regiones
ÁREA DE REGIONES CUADRANGULARES
REGIÓN CUADRANGULAR
Es una región plana cuyo contorno es un cuadrilátero.
Para nuestro estudio sólo trabajaremos con cuadriláteros convexos.
POSTULADO :
El área de una región cuadrada es igual a la longitud de su lado elevado al cuadrado.
TEOREMAS
☛ El área de una región rectangular es igual al producto de dos de sus lados no congruentes.
☛ El área de una región paralelográmica es igual al producto de uno de sus lados por la altura relativa a ella.
☛ El área de una región limitada por un trapecio es igual a la semisuma de las bases, multiplicado por la altura.
FÓRMULA GENERAL :
El área de una región cuadrangular es igual al semiproducto de las longitudes de sus diagonales multiplicando con el seno de la medida del ángulo determinado por dichas diagonales.
ÁREA DE UNA REGIÓN TRAPECIAL
El área de una región trapecial es igual al producto de la semisuma de las longitudes de las bases con la longitud de la altura de dicho trapecio.
• La razón de las áreas de una región cuadrangular ya sea convexa o no convexa con la región que se determina al considerar los puntos medios de los lados del cuadrilátero inicial es 2.
• Al trabajar con regiones trapeciales, si está trazada una diagonal se debe trazar la otra diagonal y aplicar el correspondiente teorema.
ÁREA DE UNA REGIÓN PARALELOGRÁMICA
ÁREA DE UNA REGIÓN ROMBOIDAL
El área de una región romboidal es igual al producto de las longitudes de un lado y a la altura relativa a dicho lado.
ÁREA DE UNA REGIÓN ROMBAL :
El área de una región rombal es igual al semiproducto de las longitudes de sus diagonales.
ÁREA DE UNA REGIÓN RECTÁNGULAR :
El área de una región rectangular es igual al producto de las longitudes de dos de sus lados consecutivos.
ÁREA DE UNA REGIÓN CUADRADA :
El área de una región cuadrada es igual al cuadrado de la longitud de su lado.
FÓRMULAS ADICIONALES
ÁREA DE UNA REGIÓN CUADRANGULAR CIRCUNSCRITA A UNA CIRCUNFERENCIA
El área de un cuadrilátero circunscrito a una circunferencia es igual al semiperímetro multiplicado por el inradio.
ÁREA DE UNA REGIÓN CUADRANGULAR INSCRITA EN UNA CIRCUNFERENCIA
El área de una región cuadrilátera inscrita en una circunferencia es igual a la raíz cuadrada del producto de las diferencias del semiperímetro de dicha región cuadrilátera con la longitud de cada uno de sus lados.
ÁREA DE UNA REGIÓN CUADRANGULAR INSCRITA Y CIRCUNSCRITA A UNA CIRCUNFERENCIA :
El área de una región cuadrilátera inscrita y circunscrita a una circunferencia es igual a la raíz cuadrada del producto de las longitudes de sus lados.
Cuando en un problema consideren la comparación de las áreas de dos regiones, se sugiere trabajar con regiones comunes o tomar en cuenta regiones conocidas.
PROPIEDADES DE ÁREAS EN REGIONES CUADRANGULARES
PROPIEDADES PARA TRAPEZOIDES :
El área de la región de un cuadrilátero es igual al doble del área de la región del cuadrilátero que se forma al unir los puntos medios de los lados de dicho cuadrilátero.
PROPIEDADES PARA TRAPECIOS
Al trabajar con regiones trapeciales, si está trazada una diagonal se debe trazar la otra diagonal y aplicar el correspondiente teorema.
PROPIEDADES PARA PARALELOGRAMOS
El área de una región paralelográmica se calcula como el producto de un lado y la altura relativa a dicho lado, además como el producto de dos lados consecutivos y el seno del ángulo formado por dichos lados.
EN UN POLÍGONO REGULAR :
El área de la región de un polígono regular es igual al semiproducto de su perímetro y de su apotema.
PROBLEMAS RESUELTOS
PREGUNTA 1 :
Se tiene un triángulo rectángulo isósceles y un cuadrado, cuyas regiones son equivalentes. Calcule la relación de la hipotenusa y la diagonal del cuadrado.
A) 1
B) √2
C) 2√2
D) 3
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 2 :
En un trapecio isósceles ABCD. Si AB=5, BC=4 y AD=10.
Calcule el área del trapecio.
A) 25u²
B) 26u²
C) 27u²
D) 28u²
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 3 :
En el gráfico, ABCD es un rectángulo donde AB=3 y BC=4. Calcula el área de la región sombreada.
A) 13,5
B) 14,5
C) 15,5
D) 16,5
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 4 :
Se tiene el paralelogramo ABCD, AB=6, BC=10, una de las alturas es 8. Calcule la otra altura.
A) 1,5
B) 2,5
C) 2
D) 3
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 5 :
Se tiene un trapecio ABCD, se traza BD de tal manera que la m∢CBD=35º, m∢BCD=110º y AD=2BC=2CD. Calcule la medida del ángulo BAD.
A) 40º
B) 45º
C) 50º
D) 55º
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 6 :
A) 3√3/4 cm
B) √3 cm
C) 3√3/5 cm
D) 3√3/2 cm
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 7 :
Sobre un segmento AB se ubica el punto medio C y sobre BC se ubica el punto D, desde C, D y B se levantan perpendicularmente CF, DG y BH de 10 m de longitud cada uno. Si el área de la región AFGD es igual al área de la región DGHB, calcula CD si AB=12 m.
A) 1,5
B) 2
C) 2,5
D) 3,5
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 8 :
En la figura, AB//CD y AD//BC, las áreas de las regiones triangulares BTF y ATD son 16 cm² y 25 cm² respectivamente. Halle el área de la región ABCD
A) 89 cm²
B) 88 cm²
C) 85 cm²
D) 80 cm²
E) 90 cm²
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 9 :
Halle el área de la región sombreada:
A) 24 u²
B) 96 u²
C) 48 u²
D) 98 u²
E) 100 u²
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 10 :
En una circunferencia de radio cuatro, se inscribe un cuadrado, luego se construye exteriormente los triángulos equiláteros formándose un octógono del cual nos piden el área.
A) 32(√3 + 1)
B) 32(√2 + 1)
C) 16(√2 + 1)
D) 32(√5 + 1)
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 11 :
En un trapecio ABCD, cuyas bases BC y AD miden 19cm y 27cm respectivamente. Si P es un punto de AD tal que al unir con el punto C resultan dos regiones equivalentes en el trapecio ABCD. Calcule (en cm) la longitud de AP.
A) 4
B) 8
C) 3
D) 5
E) 6
RESOLUCIÓN :
Rpta. : "A"
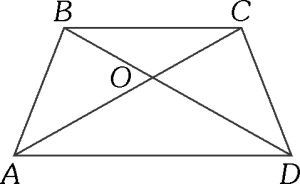
PREGUNTA 12 :
En la figura adjunta, ABCD es un trapecio, donde las diagonales determinan los triángulos AOD y BOC de áreas 25 m² y 16 m², respectivamente. Calcular el área del trapecio.
A) 66 m²
B) 70 m²
C) 81 m²
D) 91 m²
E) 101 m²
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 13 :
Por el vértice B de un rectángulo ABCD se traza una recta perpendicular a BD. Si los vértices A y C distan de dicha recta en 15 m y 10 m respectivamente, el área de dicha región rectangular, en m², es:
A) 125√6
B) 120√6
C) 110√6
D) 130√3
E) 135√3
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 14 :
Es un cuadrilátero ABC, el punto P divide al segmento AC en la razón 1/3 sobre 3 donde AP<PC. Si las áreas de las regiones triangulares ABD y BDC se miden 70 m² y 30 m², respectivamente, entonces el área de la región triangular PBD en m² es
A) 45
B) 44
C) 42
D) 40
E) 39
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 15 :
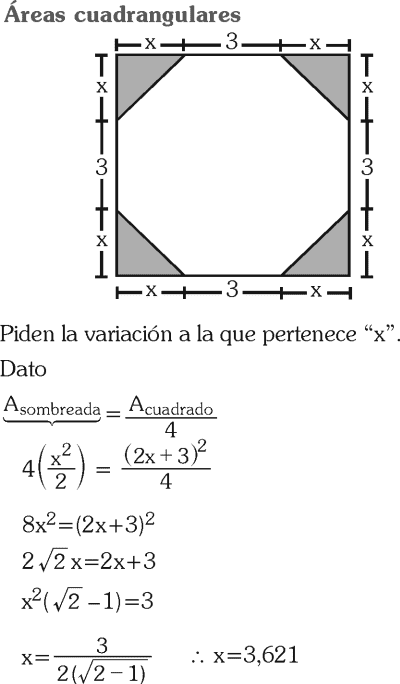
En el gráfico, la suma de las áreas de las regiones sombreadas isósceles es igual a la cuarta parte del área de la región cuadrada ABCD; encuentra a qué intervalo pertenece “x”.
A) 0,5 < x < 1
B) 1 < x < 2,5
C) 2,5 < x < 3,1
D) 3,1 < x < 4
RESOLUCIÓN :
Rpta. : "D"
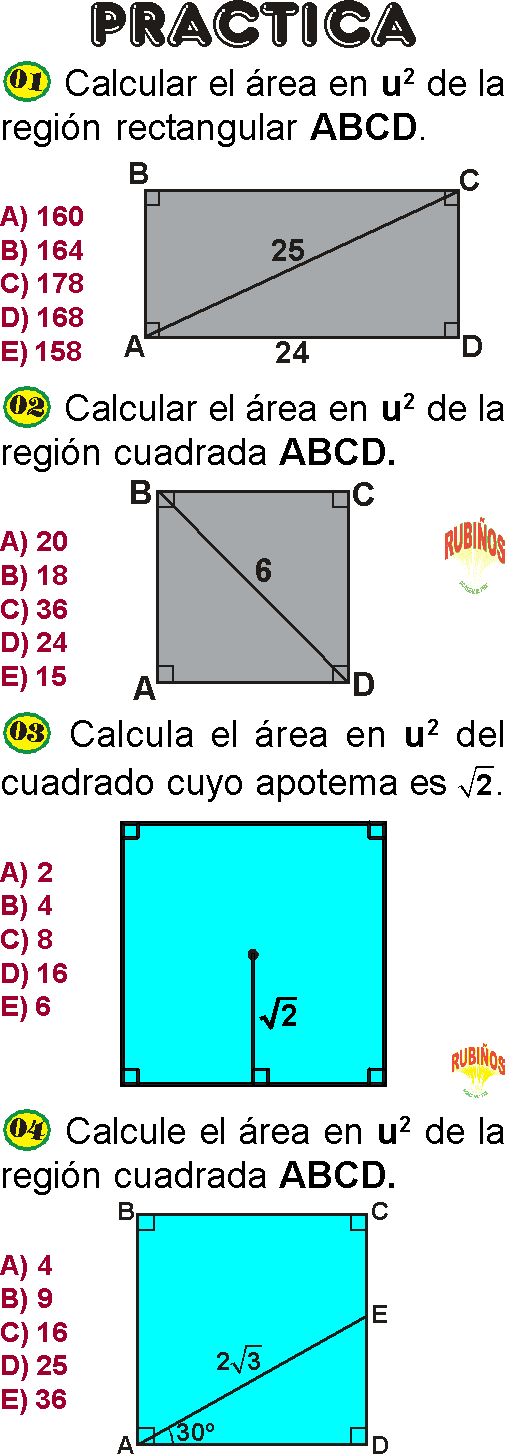
PRACTICA
PREGUNTA 1 :
En un trapecio ABCD circunscrito a una circunferencia de radio 3 u, los lados no paralelos AB y CD miden 7 u y su respectivamente. Calcule el área de la región trapecial ABCD.
A) 35 u2
B) 25 u2
C) 45 u2
D) 32 u2
E) 26 u2
Rpta. : "C"
PREGUNTA 2 :
En un rombo cuyo lado mide 5 m y uno de los ángulos agudos es igual a 53°. Calcule el área de la región rombal.
A) 24 m2
B) 18 m2
C) 20 m2
D) 32 m2
E) 30 m2
Rpta. : "C"
PREGUNTA 3 :
Calcule el área de la región cuadrada inscrita en una semicircunferencia de 3√5 m de radio.
A) 24 m2
B) 12 m2
C) 18 m2
D) 36 m2
E) 8 m2
Rpta. : "C"
PREGUNTA 4 :
Una región triangular y trapecial tienen áreas y alturas iguales. Si la base de la región triangular mide 18 m, calcule la longitud de a base media del trapecio.
A) 10 m
B) 12 m
C) 9 m
D) 8 m
E) 16 m
Rpta. : "C"
PREGUNTA 5 :
En una región rombal ANCD, la m∢A = 74° y su perímetro es 20. Calcule el área de dicha región.
A) 42 u2
B) 24 u2
C) 35 u2
D) 36 u2
E) 18 u2
Rpta. : "B"
PREGUNTA 6 :
En la figura, CF = 3 y EC = 6. Calcule el área de la región cuadrada ABCD.
A) 169
B) 196
C) 125
D) 150
E) 144
PREGUNTA 7 :
Si el radio de la circunferencia inscrita en un rombo mide 7 m, halle el área de la región rombal si su perímetro es 64 m.
A) 100 m2
B) 140 m2
C) 160 m2
D) 224 m2
E) 280 m2
PREGUNTA 8 :
Halle la longitud de la diagonal de un cuadrado si el área de su región es 12 u2.
A) 3√6
B) 3
C) 2√3
D) 3√3
E) 2√6
PREGUNTA 9 :
Las diagonales de un trapezoide simétrico miden 20 m y 30 m. Calcule el área de su región.
A) 150√3 m2
B) 150 m2
C) 200 m2
B) 300√3 m2
E) 300 m2
PREGUNTA 10 :
Se tiene un trapecio de bases AB = 28 m y DC = 64 m, se toman los puntos M y P sobre las bases AB y DC respectivamente. Si el segmento PM divide al trapecio en dos cuadriláteros equivalentes y PD = 24 m, calcule MB.
A) 8 m
B) 12 m
C) 6 m
D) 3 m
E) 9 m
PREGUNTA 11 :
Calcule el área de una región rombal cuyo lado mide 5 m si la suma de las longitudes de sus diagonales es 14 m.
A) 20 m2
B) 35 m2
C) 48 m2
D) 24 m2
E) 40 m2
PREGUNTA 12 :
En una región rombal ABCD, la m∢B = 106º y su perímetro es 40. Calcule el área de dicha región.
A) 85
B) 90
C) 84
D) 48
E) 96
PREGUNTA 13 :
En una región romboidal dos de sus lados miden 12 y 18, una de sus alturas mide 15. Calcule el área de dicha región.
A) 180
B) 270
C) 150
D) 140
E) 200
PREGUNTA 14 :
En una región rectangular ABCD, BC = 4AB y su perímetro es 50. Calcule el área de dicha región.
A) 130
B) 100
C) 120
D) 140
E) 110
