ÁNGULOS VERTICALES EJERCICIOS RESUELTOS PDF
OBJETIVOS :
✎ Definir y ejemplificar los ángulos verticales de elevación, depresión y de observación.
✎ Contextualizar en lo cotidiano los ángulos verticales.
✎ Utilizar las definiciones de los ángulos verticales y los casos de resolución de triángulos rectángulos en la resolución de los problemas dirigidos y tipo examen de admisión.
ÁNGULOS VERTICALES
Se llama así a aquellos ángulos que están contenidos en un plano vertical.
Los ángulos verticales son determinados en el instante en el cual se realiza una observación, estos ángulos se determinan en el punto desde el cual se está observando entre dos líneas imaginarias trazadas por dicho punto y que permitirán la observación; según su ubicación estos ángulos serán ángulos de elevación, ángulos de depresión o ángulos de observación.
ÁNGULO DE ELEVACIÓN
Es el ángulo formado por la línea horizontal y la línea visual cuando el objeto se encuentra por encima de la línea horizontal. Para determinar un ángulo de elevación debemos de trazar una línea horizontal que pasa por el ojo del observador y la línea visual está por encima de la horizontal.
ÁNGULO DE DEPRESIÓN
Es el ángulo formado por la línea horizontal y la línea visual cuando el objeto se encuentra por debajo de la línea horizontal. Para determinar el ángulo de depresión debemos de trazar una línea horizontal que pasa por el ojo del observador y la línea visual que está debajo de la horizontal.
ÁNGULO DE OBSERVACIÓN
Es el ángulo formado por dos líneas visuales , También se denomina ángulo de visibilidad.
El instrumento que nos ayuda a medir los ángulos verticales, así mismo los ángulos horizontales, es el teodolito, que tiene aplicación sobre todo en la industria de la construcción
TEODOLITO :
El teodolito es un instrumento de medición mecánico-óptico universal que sirve para medir ángulos verticales y, sobre todo, horizontales, ámbito en el cual tiene una precisión elevada.
Con otras herramientas auxiliares puede medir distancias y desniveles. Es portátil y manual; está hecho para fines topográficos e ingenieros, sobre todo en las triangulaciones. Con ayuda de una mira y mediante la taquimetría, puede medir distancias. Un equipo más moderno y sofisticado es el teodolito electrónico, más conocido como estación total. Básicamente, el teodolito actual es un telescopio montado sobre un trípode y con dos círculos graduados, uno vertical y otro horizontal, con los que se miden los ángulos con ayuda de lentes.
CONSIDERACIONES PARA LA RESOLUCIÓN DE PROBLEMAS
☛ La estatura de las personas se deberá considerar hasta sus ojos.
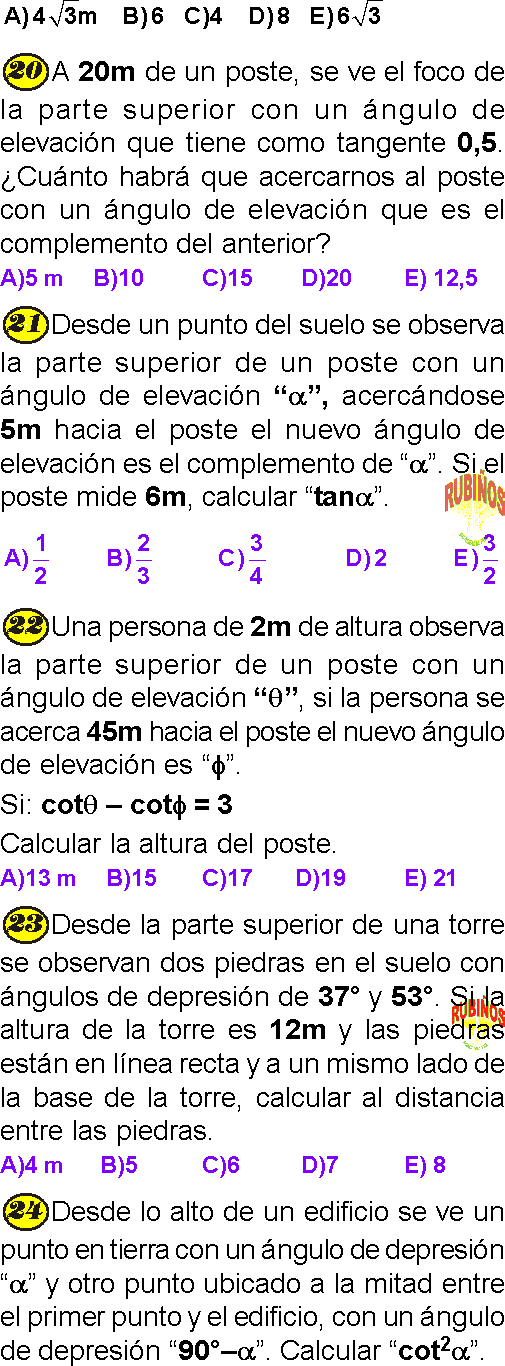
☛ Toda persona u objeto que posea una altura, será considerada perpendicular al nivel del suelo, a no ser que el problema indique otra situación .
☛ De no indicarse desde que altura se realiza la observación y no siendo esta altura la incógnita del problema, se deberá considerar que se está observando desde un punto del suelo .
PRIMERA PRACTICA
PREGUNTA 1 :
Un poste de 2m de longitud es apoyado sobre una pared, formando con éste un ángulo de 30°, calcula la distancia entre la parte más baja del poste y la pared.
a) 5
b) 4
c) 8
d) 6
e) 3
Rpta. : "E"
PREGUNTA 2 :
Un observador se encuentra a 4m de la base de un poste de 3m de altura. ¿Cuál es el ángulo de elevación respectivo?
a) 30°
b) 53°
c) 45°
d) 60°
e) 37°
Rpta. : "E"
PREGUNTA 3 :
La parte superior de un edificio de 24 m de altura es observada bajo un ángulo de elevación de 53°. ¿Cuál es la distancia entre el observador y el pie del edificio?
a) 18m
b) 16m
c) 12m
d) 19m
e) 15m
Rpta. : "A"
PREGUNTA 4 :
A 40 m del pie de un poste la elevación angular para lo alto del mismo es de 37°. ¿Cuál es la altura del poste?
a) 24 m
b) 20 m
c) 30 m
d) 28 m
e) 40 m
Rpta. : "C"
PREGUNTA 5 :
Desde la parte superior de un morro de 15 m de altura se observa un objeto que está ubicado a 20 m del pie del morro. ¿Cuál es el ángulo de depresión?
a) 30°
b) 45°
c) 37°
d) 16°
e) 53°
Rpta. : "E"
PREGUNTA 6 :
Desde un punto en tierra , se divisa lo alto de un edificio con un ángulo de elevación β . Si la altura del edificio es "h", ¿A qué distancia del edificio se encuentra el punto de observación?.
A) hsenβ
B) hcosβ
C) htanβ
D) hcotβ
Rpta. : "D"
PREGUNTA 7 :
Desde lo alto de un faro, se observa un mismo lado, dos barcos anclados, con un ángulo de depresión de 53° y 37°. Si los barcos están separados una distancia de 14m, ¿Cuál es la altura del faro ?.
A) 16m
B) 12
C) 24
D) 32
E) 8
Rpta. : "C"
PREGUNTA 8 :
Desde lo alto y bajo de un muro se observa lo alto de un poste con ángulos de elevación de 37° y 45°, respectivamente. Si la distancia entre muro y poste es 8m , halle la suma de sus alturas.
A) 10m
B) 20
C) 12
D) 24
E) 6
Rpta. : "A"
PREGUNTA 9 :
Una persona de 1,75m de altura observa la parte superior de una torre con un ángulo de elevación de 37°. Después de avanzar 5m en dirección a la torre, desde el extremo superior de la persona con un ángulo de depresión de 45°. Calcular la altura de la torre.
A) 15m
B) 15,5
C) 15,75
D) 16,75
E) 17
Rpta. : "D"
PREGUNTA 10 :
Desde el extremo superior de una torre de 24m de altura se observan los puntos “A” y “B” con ángulos de depresión de 37° y 53° respectivamente, si los puntos A y B se encuentran alineados con la torre. Determinar la distancia entre dichos puntos .
A) 14m
B) 18
C) 32
D) 6
E) 16
Rpta. : "A"
PREGUNTA 11 :
La elevación de una torre desde un punto A al oeste de ella es 60° y desde un punto B al sur de A , la elevación es de 30° . Si la torre tiene 75 m de altura ,Determinar la distancia comprendida entre A y B .
A) 50√6
B) 30√3
C) 32√6
D) 6√31
E) 16√2
Rpta. : "A"
PREGUNTA 12 :
Calcule la medida aproximada del ángulo de elevación del Sol, cuando una persona de h metros de estatura proyecta una sombra de 2h metros de longitud en un terreno a nivel.
A) 15°
B) 18°
C) 18,5°
D) 26,5°
E) 30°
Rpta. : "D"
PREGUNTA 13 :
Una persona de 1,65 m de estatura observa la base de un poste de luz con un ángulo de depresión de 37° y la parte superior de este con un ángulo de elevación cuya tangente es 5. Calcule la altura del poste.
A) 12 m
B) 12,3 m
C) 13 m
D) 12,65 m
Rpta. : "D"
PREGUNTA 14 :
Un niño observa la parte superior de un edificio con un ángulo de elevación de 18,5°. Si el niño se encuentra a 24m del pie del edificio, ¿cuánto deberá caminar (en m)en dirección del edificio, para obtener la parte superior de este con un ángulo de 26,5°?
A) 4
B) 8
C) 10
D) 12
E) 16
Rpta. : "B"
PREGUNTA 15 :
Una estatua de 5 metros de altura descansa sobre una pedestal de 4m de alto. Si desde un punto en el piso se observa la cabeza de la estatua con un ángulo de elevación 2θ y el ángulo de visual de la estatua es θ, halle la distancia del observador al pedestal y cos2θ.
A) 6 y 0,6
B) 7 y 0,7
C) 8 y 0,8
D) 10 y 0,9
E) 12 y 0,8
Rpta. : "E"
PREGUNTA 16 :
Un avión que vuela horizontalmente observa en tierra una casa con ángulo de depresión β. Se desplaza a partir de ese instante una distancia igual al triple de su altura y el nuevo ángulo de depresión de la casa crece y es igual al complemento de β. Calcule cot²β + tan²β.
A) 11
B) 12
C) 13
D) 15
Rpta. : "A"
PREGUNTA 17 :
Desde un avión que vuela sobre la línea que separa a dos ciudades A y B, se observa con ángulos de depresión de 30° y 45°. Halle la altura a la cual se encuentra el avión, sabiendo que la distancia que separa a las dos ciudades es 125( √3 + 1) km.
A) 120 km
B) 110 km
C) 125 km
D) 150 km
Rpta. : "C"
PREGUNTA 18 :
Desde un globo aerostático, una persona observa en una misma dirección dos barcos con ángulos de depresión de 53° y 45°, respectivamente. Si los barcos distan entre sí 80 m, calcule la altura de vuelo del globo.
A) 320 m
B) 340 m
C) 350 m
D) 600 m
Rpta. : "A"
PREGUNTA 19 :
Un avión vuela en línea recta y horizontalmente a una altura de 2420 m. Desde un punto en tierra es observado con un ángulo de elevación de 53°. Calcule la distancia entre ese punto y el avión.
A) 2400 m
B) 3200 m
C) 3000 m
D) 3025 m
Rpta. : "D"
PREGUNTA 20 :
Desde el último piso de un edificio de altura 3h se observa la parte superior de una torre de altura 5h con un ángulo de elevación θ y la parte baja de esa torre con un ángulo de depresión de 30°. Calcule cotθ.
A) √3/2
B) 3/2
C) 5/2
D) √3/9
Rpta. : "A"
SEGUNDA PRACTICA
PREGUNTA 1 :
La elevación angular de la parte superior de una torre vista desde el pie de un poste es de 60°, y desde la parte superior del poste, que tiene 30 m de altura, el ángulo de elevación mide 30°. Luego la altura de la torre es:
a) 15 m
b) 30 m
c) 45 m
d) 60 m
e) 75 m
Rpta. : "C"
PREGUNTA 2 :
Desde un punto en el suelo se observa la parte más alta de una torre con un ángulo de elevación de 60°, si se retrocede 40 m y se vuelve a observar la parte más alta, el ángulo de elevación es de 30°. Hallar la altura de la torre.
a) 20√3 m
b) 10√3 m
c) 30 m
d)15√3 m
e) 10 m
Rpta. : "A"
PREGUNTA 3 :
Una persona ubicada en la parte más alta de un edificio observa a dos puntos opuestos a ambos lados del edificio con ángulos de depresión de 37° y 53°. Si los puntos distan entre sí 20 metros, hallar la suma de las visuales.
a) 20 m
b) 22 m
c) 24 m
d) 26 m
e) 28 m
Rpta. : "A"
PREGUNTA 4 :
Desde lo alto de un edificio se ve un punto en tierra con un ángulo de depresión "α", y a otro punto ubicado a la mitad entre el primer punto y el edificio con un ángulo de depresión “90°–α”. Calcular "Ctg α".
a) √2
b) √2/2
c) 2√2
d) √2/4
e) 1
Rpta. : "A"
PREGUNTA 5 :
Un avión vuela horizontalmente a una altura constante, antes de pasar sobre dos puntos en tierra “A” y “B” los observa con ángulos de depresión de 45° y 37° respectivamente. Cuando está sobre “B” es visto desde “A” con un ángulo de elevación “α". ¿Cuánto vale Tgα?
a) 1
b) 2
c) 3
d) 4
e) 6
Rpta. : "C"
PREGUNTA 6 :
La estatura de un hombre es 1,68 m. Observa su sombra a las 2 de la tarde, asumiendo que amanece a las 6 de la mañana y que él sol sigue una trayectoria circular sobre el hombre. ¿Cuánto mide su sombra aproximadamente?
a) 79 cm
b) 48 cm
c) 97 cm
d) 84 cm
e) 63 cm
Rpta. : "C"
PREGUNTA 7 :
Desde el décimo piso de un edificio de 16 pisos, se observa un punto en el suelo con un ángulo de depresión “θ”. De la azotea del edificio se observa el mismo punto con un ángulo de depresión igual al complemento de θ. Hallar: Ctg θ.
a) 2/3
b) 1/3
c) 1
d) 4/3
e) 5/3
Rpta. : "D"
PREGUNTA 8 :
Un niño de 100cm de estatura mira un OVNI con un ángulo de elevación de 45°. Luego el OVNI pasa sobre el niño volando a una altura constante y es visto nuevamente ahora con un ángulo de elevación de 53°. Si la distancia horizontal entre la primera y segunda observación fue de 182 m. Hallar a que altura volaba el OVNI.
a) 104 m
b) 105 m
c) 106 m
d) 204 m
e) 183 m
Rpta. : "B"
PREGUNTA 9 :
Un mono se encuentra a 24 m de altura en el tronco de una palmera, y ve a una mona que está en el suelo con un ángulo de depresión de 53°. Luego, ambos se dirigen en forma simultánea hacia la base la palmera, y cuando la mona ha avanzado la mitad de la distancia que la separaba de la palmera inicialmente mira al mono con un ángulo de elevación de 45°; entonces la distancia que los separa en ese instante es:
a) 9√2/2 m
b) 9 m
c) 9√2m
d)18√2 m
e) 18 m
Rpta. : "C"
PREGUNTA 10 :
Un avión que vuela a una altura constante de 6000 m pasa sobre una ciudad, 2 minutos después es visto desde la ciudad, con un ángulo de elevación de 37°, ¿cuál es la velocidad constante del avión en km/h?
a) 480
b) 120
c) 960
d) 240
e) 360
Rpta. : "D"
PREGUNTA 11 :
Desde un punto se observa la parte más alta de un edificio con un ángulo de elevación “θ", si después de avanzar las 2/3 partes de la distancia original que separaba al observador del pie del edificio, el ángulo de elevación fue el complemento de "θ". Calcular "θ".
a) 15°
b) 45°
c) 60°
d) 30°
e) 22°30'
Rpta. : "D"
PREGUNTA 12 :
Una persona colocada a 36 m de una torre, observa su parte más alta con un ángulo de elevación “α" (Tgα =7/12). ¿Qué distancia habría que alejarse para que el ángulo de elevación sea θ? Donde: Tgθ = 1/4
a) 12 m
b) 13 m
c) 48 m
d) 15 m
e) 20 m
Rpta. : "C"
PREGUNTA 13 :
Una persona se dirige a un edificio, y observa lo alto del mismo bajo un ángulo de elevación “x”; después de caminar 10 m observa la misma altura con un ángulo de elevación “θ". Si la altura del edificio es 30 m, hallar: Tgx( Tgθ + 0,333...)
a) 1
b) 2
c) 3
d) 4
e) 5
Rpta. : "A"
PREGUNTA 14 :
Un avión que inicialmente se encuentra a 2700 m de altura, sobre un objeto, empieza a caer con un ángulo de 37° por debajo de la línea horizontal, avanzando 500 m luego retoma su posición horizontal avanzando una distancia “x” y el piloto observa el objeto con un ángulo de depresión de 45°. Calcular “x”.
a) 2400 m
b) 1800 m
c) 2400√2
d) 2100√2
e) 2000 m
Rpta. : "E"
PREGUNTA 15 :
Dos personas de estaturas “H” y “h” (H>h) se encuentran paradas frente a frente separadas una cierta distancia. La persona de menos estatura observa la cabeza de la otra persona con un ángulo de elevación α y sus pies con un ángulo de depresión "β". Hallar: "H/h".
a) 1+TgαTgβ
b) 1+TgαCtgβ
c) 1+CtgαTgβ
d) 1+CtgαCtgβ
e) 1+SenαCosβ
Rpta. : "B"
PREGUNTA 16 :
Desde lo alto de un faro a 15m sobre el nivel del mar se observa una boya con un ángulo de depresión cuya tangente es 3/2; desde la base del faro a 8 m sobre el nivel del mar se vuelve a observar la boya, con un ángulo de depresión “θ”. Calcule el valor de "Tgθ"
a) 5/4
b) 4/5
c) 3/4
d) 4/3
e) 3/5
Rpta. : "B"
PREGUNTA 17 :
Un ratón observa el borde superior de un muro con un ángulo de elevación de 37°; luego avanza 28 m acercándose al muro en línea recta y, lo vuelve a observar con un ángulo de elevación de 53°. Si el ratón tarda 3 segundos en llegar a la base del ° muro desde su segunda posición, determine la velocidad constante en m/seg con que se desplaza el roedor.
a) 18
b) 16
c) 14
d) 12
e) 10
Rpta. : "D"
PREGUNTA 18 :
Desde dos puntos “P” y “Q” situados al Sur y al Este de un poste de luz se observa su foco con ángulos de elevación que son complementarios. Si la distancia PQ es igual al triple de la altura del poste, y uno de los ángulos de elevación mencionados mide “θ".
Hallar: Tgθ + Ctgθ
a) 1
b) 3
c) 9
d) 11
e) 7
Rpta. : "D"
PREGUNTA 19 :
Subiendo por un camino inclinado un ángulo de 37º respecto a la horizontal, se divisa lo alto de un poste con un ángulo de elevación de45º. Si el poste se encuentra a 20m del punto de observación; ¿Cuál es la altura del poste?
A) 2m
B) 3m
C) 6m
D) 4m
E) 8m
Rpta. : "D"
PREGUNTA 20 :
Cuando observamos una torre desde un punto en el terreno distante 2 m más que su altura el ángulo de elevación mide “α”, pero si se observa de otro punto en el terreno distante 2 m menos que su altura el ángulo de elevación mide “2α”. Luego la altura de la torre es:
a) √7 m
b) ( √6 –1) m
c) ( √7 –1) m
d) ( √6 +1) m
e) ( √7 +1) m
Rpta. : "E"
PREGUNTA 21 :
Una antena de radio de 15m. de longitud se encuentra en la azotea de un edificio. Desde un punto del plano horizontal que pasa por la base del edifico las elevaciones angulares de la parte superior e inferior de la antena son “α” y “β” respectivamente.
Si: tanα = 0,76 y tanβ=0,19 Determinar (en m) la altura del edifico.
A) 4
B) 5
C) 6
D) 7
E) 8
Rpta. : "B"
PREGUNTA 22 :
Desde un punto de tierra se ve lo alto de una torre con un ángulo de elevación “θ”. Nos acercamos una distancia igual a la altura de la torre y el ángulo de elevación es ahora 37º. Calcule: ctgθ (Tomar: sen37º = 0,6)
A) 53
B) 43
C) 73
D) 3
E) 2
Rpta. : "C"
PREGUNTA 23 :
Una persona colocada a la orilla del rio ve un árbol plantado sobre la ribera opuesta bajo un ángulo de elevación de 60º se aleja 40mts, y nuevo ángulo de elevación mide 30º ¿Cuál es la altura del árbol?
A) 43,6
B) 30,6
C) 34,6
D) 36,4
E) 38,4
Rpta. : "D"
PREGUNTA 24 :
Un avión que esta por aterrizar observa en su misma trayectoria la pista de aterrizaje de extensión igual al doble de la altura a la que se encuentra, si ve el extremo más alejado con ángulo de depresión de 22º30’ .Calcule con que ángulo observa el otro extremo.
A) 22º30’
B) 67º30’
C) 90º
D) 60º
E) 120º
Rpta. : "D"
PREGUNTA 25 :
Subiendo por un camino inclinado de ángulo ψ respecto a la horizontal, se observa lo alto de una torre con un ángulo de elevación 2ψ, de modo que se verifica que la torre mide a metros y la visual b metros. Calcule el valor de cotψ.
A) a/b
B) 2a/b
C) b/a
D) a/2b
Rpta. : "C"
PREGUNTA 26 :
Desde el pie de un poste, el ángulo de elevación de la parte más alta de una palmera es 53°, y desde la parte superior del poste que tiene 6 m de altura, el nuevo ángulo de elevación es de 18°30'. Calcule la altura de la palmera.
A) 8 m
B) 10 m
C) 12 m
D) 15 m
Rpta. : "A"
PREGUNTA 27 :
Sobre un peñasco situado en la ribera de un río se levanta una torre de 120 m de altura. Desde el extremo superior de la torre, el ángulo de depresión de un punto situado en la orilla opuesta es de 60° y desde la base de la torre, el ángulo de depresión del mismo punto es de 30°. Calcule la altura del peñasco, en metros.
A) 30
B) 50
C) 60
D) 90
Rpta. : "C"
PREGUNTA 28 :
Un topógrafo observa con un teodolito la cima de un peñasco de 69,10 m de altura con un ángulo de elevación cuya tangente es 3/4. Interesado en observar mejor la cima del peñasco, se aproxima a este una cierta distancia siguiendo una trayectoria recta en la misma dirección en la que se encontraba inicialmente, por lo que la tangente del nuevo ángulo de elevación es 5/4. Si el punto de visualización del teodolito está a 1,60 m de altura del suelo, ¿cuántos metros se aproximó el topógrafo al peñasco?
A) 37 m
B) 27 m
C) 36 m
D) 26 m
Rpta. : "C"