RAZONAMIENTO GEOMÉTRICO EJERCICIOS RESUELTOS PDF
PREGUNTA 1 :
En la figura, las curvas son congruentes entre sí. Hallar el área de la región sombreada.
.png)
A) 20
B) 17,5
C) 15π
D) 30
E) 15√3
RESOLUCIÓN :
.png)
Rpta. : "D"
PREGUNTA 2 :
Los radios de los círculos mostrados forma una progresión aritmética de razón 2. Si la suma de todos los diámetros es igual a 200. Calcular el perímetro de la región sombreada.
.png)
A) 100 π
B) 150π
C) 200π
D) 400π
E) 50
RESOLUCIÓN :
.png)
Rpta. : "C"
PREGUNTA 3 :
Calcular “α”
.png)
A) 30º
B) 60º
C) 45º
D) 37º
E) 53º
RESOLUCIÓN :
.png)
Rpta. : "C"
PREGUNTA 4 :
Del gráfico adjunto L1//L2, calcular “x”.
.png)
A) 20
B) 25
C) 60
D) 40
E) 45
RESOLUCIÓN :
.png)
Rpta. : "D"
PREGUNTA 5 :
Hallar “α”, para el cual la caída del agua en el vaso es inminente.
.png)
A) 30º
B) 37º
C) 45º
D) 60º
E) 53º
RESOLUCIÓN :
.png)
Rpta. : "C"
PREGUNTA 6 :
En la figura, calcular “β”
.png)
A) 30º
B) 15º
C) 10º
D) 18º
E) 5º
RESOLUCIÓN :
.png)
Rpta. : "D"
PREGUNTA 7 :
Si la recta “L” es perpendicular a las rectas paralelas “L1” y “L2” , OP es bisectriz del ángulo AOB, calcular: “x”.
.png)
A) 10
B) 15
C) 20
D) 30
E) 45
RESOLUCIÓN :
.png)
Rpta. : "B"
PREGUNTA 8 :
“E” punto medio de BC. ABCD es un cuadrado. Hallar x
.png)
A) 8º
B) 15º
C) 16º
D) 20º
E) 37º
RESOLUCIÓN :
.png)
Rpta. : "B"
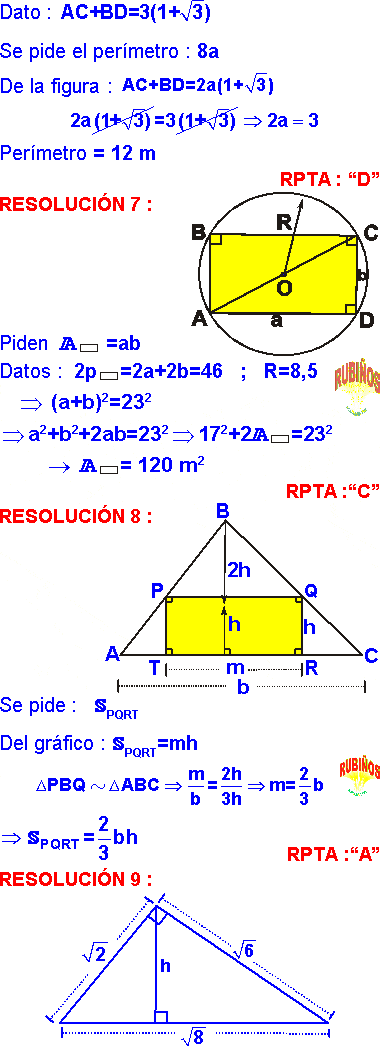
PREGUNTA 9 :
En una institución educativa se quiere construir un campo deportivo rectangular, para lo cual se diseña una maqueta, donde el largo y el ancho del rectángulo que representa el campo deportivo miden 20 cm y 10 cm respectivamente. Si la escala empleada para diseñar la maqueta es de 1 : 500, ¿cuál es el perímetro real del campo deportivo?
A) 250 m
B) 300 m
C) 120 m
D) 350 m
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 10 :
Se tiene una escalera de 2,5 m apoyada en una pared vertical; el pie de la escalera está a 0,7 m de la pared. Si la parte superior se desliza 0,4 m, ¿cuánto se desliza la parte interior?
A) 2,3
B) 1,5
C) 0,8
D) 0,9
E) 2,5
RESOLUCIÓN :
.png)
Rpta. : "C"
PREGUNTA 11 :
A una pieza cuadrada de papel se le hacen dos dobleces y luego se la perfora, tal como muestra la figura.
¿Cuál de las siguientes figuras es la que se obtiene al desdoblar totalmente el papel?
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 12 :
Calcular “x”, si los 2 cuadrados son congruentes.
.png)
A) 30º
B) 37º
C) 53º
D) 16º
E) 15º
RESOLUCIÓN :
.png)
Rpta. : "B"
PREGUNTA 13 :
Lenin fabricó una cometa cortando un listón de madera recto en seis piezas. Usó dos de ellas, de longitudes 114 cm y 76 cm, como diagonales tales que formaban dos triángulos rectángulos isósceles idénticos. Las piezas restantes conectaban los puntos medios de los lados de la cometa, como muestra la figura. ¿Cuánto media el listón antes de cortarlo?
A) 360 cm
B) 380 cm
C) 370 cm
D) 390 cm
RESOLUCIÓN :
.png)
Rpta. : "B"
PREGUNTA 14 :
Un teatro cuenta con 200 asientos numerados con números enteros desde 1 hasta 200. Taty compra un boleto para el asiento número 100 y su amiga Amy quiere sentarse lo más cerca de ella, pero los únicos asientos disponibles tienen numeración 76, 94, 99, 104 y 118. Si la disposición de los asientos es como se muestra en la figura, ¿qué asiento debe elegir la amiga de Taty?
A) 76
B) 104
C) 99
D) 118
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 15 :
Se corta un alambre de dos metros de longitud en dos partes para formar, con una de ellas, un triángulo equilátero y, con otra, un cuadrado. Si se quiere que la suma de las áreas de ambas figuras sea mínima, ¿a qué distancia de uno de los extremos del alambre se debe hacer el corte?
RESOLUCIÓN :
Rpta. : "B"
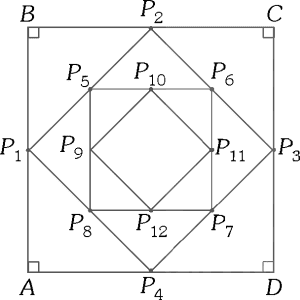
PREGUNTA 16 :
En la clase de Arte, la profesora propone hacer un cuadrado usando papel lustre de cuatro colores (azul, rojo, amarillo y verde, en ese orden). Ella da la siguiente indicación: primero, deben recortar un trozo de papel lustre de color azul de forma cuadrada y ubicar sus vértices en los puntos A, B, C y D. A continuación, deben utilizar los puntos medios de sus lados P₁, P₂, P₃ y P₄ como vértices del cuadrado de color rojo y pegar este cuadrado rojo sobre el cuadrado azul, tal como se muestra en la figura. Así, sucesivamente con el papel lustre amarillo y, finalmente, con el papel lustre verde con vértices en los puntos de P₉, P₁₀, P₁₁ y P₁₂. Halle la razón entre el perímetro del cuadrado azul y el perímetro del cuadrado verde.
A) 2√2
B) √2
C) 2
D) 4
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 17 :
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 18 :
¿Cuál es el área máxima de la región que se muestra en la figura si se sabe que su perímetro es 60 cm?
A) 196 cm²
B) 175 cm²
C) 225 cm²
D) 216 cm²
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 19 :
Renato hace rodar una lámina circular cuyo radio mide 2 cm sobre la trayectoria ABCD, desde el punto A hasta el punto D (ver figura adjunta). Si AB= 12 cm, BC=CD= 18 cm, halle la menor longitud total, en centímetros, que recorre el centro de la lámina circular.
A) 48 + π
B) 45 + π
C) 46 + π
D) 44 + π
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 20:
La figura 1 representa un vaso que tiene la forma de un cilindro circular recto cuyo radio de la base mide 4 cm y la figura 2 representa una bandeja rectangular. ¿Cuántos vasos idénticos como los de la figura 1 se pueden colocar, como máximo, sobre la bandeja representada por la figura 2, sin que estos se desborden ni se apilen uno sobre otro?
A) 10
B) 12
C) 14
D) 11
RESOLUCIÓN :
.png)
Rpta. : "D"
