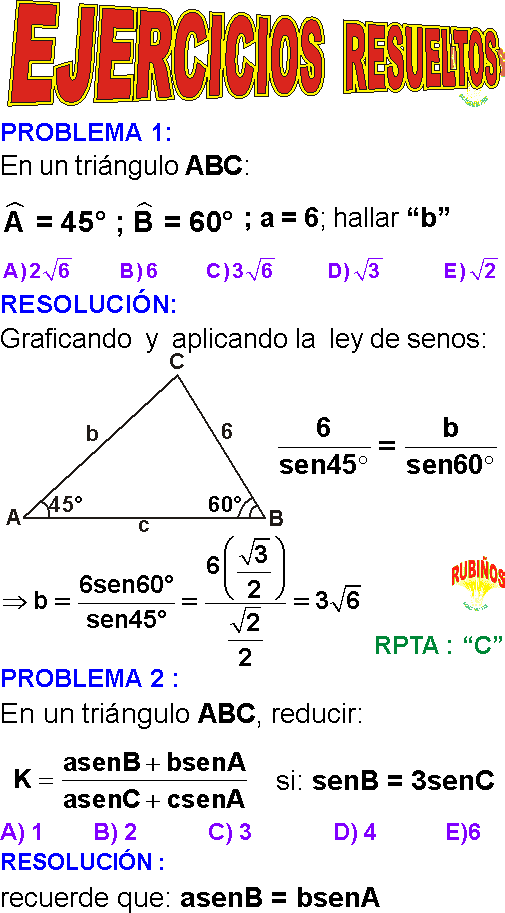
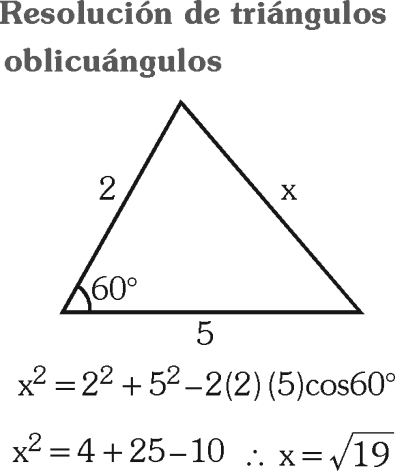
RESOLUCIÓN DE TRIÁNGULOS OBLICUÁNGULOS EJERCICIOS RESUELTOS PDF
LEY DE SENOS COSENOS PROYECCIONES Y TANGENTES
OBJETIVOS
Al finalizar la unidad, el alumno será capaz de:
☛ Determinar las medidas de los elementos básicos de un triángulo, es decir sus tres lados y tres ángulos, a partir de ciertos datos conocido.
☛ Aplicar el teorema de senos y el teorema de cosenos en la resolución de triángulos oblicuángulos.
☛ Aplicar el teorema de las proyecciones en la resolución de triángulos oblicuángulos.
A todo triángulo que sea diferente a un triángulo rectángulo se le denomina triángulo oblicuángulo.
La resolución de triángulos oblicuángulos es un medio que nos permite calcular en forma sencilla los lados y ángulos del triángulo.
Hay diferentes teoremas o leyes que permiten resolver un triángulo, las cuales se aplican dependiendo de los datos que se tenga del triángulo en estudio.
Para la resolución de triángulos oblicuángulos es importante tener presente los siguientes teoremas:
☛ Teorema de senos
☛ Teorema de cosenos
☛ Teorema de las proyecciones
☛ Teorema de tangentes
LEY DE SENOS
En todo triángulo, las medidas de cada uno de sus lados son directamente proporcionales a los senos de sus ángulos opuestos y , además , la constante de proporción es el diámetro de la circunferencia circunscrita».
LEY DE COSENOS
En todo triángulo la medida de cualesquiera de sus lados al cuadrado es igual a la suma de los cuadrados de los otros dos, menos el doble del producto de dichos lados por el coseno del ángulo que estos forman.
TEOREMA DE LA PROYECCIONES
En cualquier triángulo un lado es igual a la suma de los otros dos lados multiplicados cada uno por el Coseno del ángulo adyacente a dicho lado.
TEOREMA DE TANGENTES (LEY DE TANGENTE)
En todo triángulo , la diferencia de dos lados es a su suma como la tangente de la semidiferencia de los ángulos opuestos a dichos lados es a la tangente de la semisuma de los mismos ángulos.
¿Qué significa resolver un triángulo ?
Significa calcular las longitudes de sus lados y la medida de sus ángulos.
Para esto necesitamos conocer por lo menos la longitud de un lado junto con otras dos cantidades ya sean dos ángulos o los otros dos lados o bien un ángulo y un lado.
Así , hay cuatro posibilidades por considerar :
CASO I :
Se conoce un lado y dos ángulos.
CASO II :
Se conoce dos lados y el ángulo opuesto a uno de ellos.
CASO III :
Se conoce dos lados y el ángulo entre ellos.
CASO IV :
Se conoce tres lados.
TEOREMAS TRIGONOMÉTRICOS
☛ La ley de senos se usa para resolver los triángulos de los casos I y II.
☛ La ley de cosenos se usa para resolver los triángulos de los casos III y IV
PRACTICA PROPUESTA
PREGUNTA 1 :
En un triángulo ABC, se cumple que AB=3 m∢A=45° y m∢B=105°.
Calcula BC.
a) 2√2
b) 3√2
c) 3
d) 1/2
e) –1/2
Rpta. : "B"
PREGUNTA 2 :
Determina el mayor ángulo de un triángulo cuyos lados son proporcionales a los números 7, 8 y 13.
a) 30°
b) 60°
c) 90°
d) 120°
e) 150°
Rpta. : "D"
PREGUNTA 3 :
En un triángulo ABC se cumple:
a² = b² + c² + bc
b² = a² + c² – √2ac
Halla la medida del ángulo C
a) 15°
b) 45°
c) 75°
d) 60°
e) 30°
Rpta. : "A"
PREGUNTA 4 :
Se tiene un triángulo ABC en el que la suma de los cuadrados de los lados es el triple del cuadrado del radio de la circunferencia circunscrita a dicho triángulo.
Calcular:
Cos2A+Cos2B+Cos2C
a) 1/2
b) 1
c) 2/3
d) 3/2
e) 2
Rpta. : "D"
PREGUNTA 5 :
En un triángulo ABC, se tiene que:
a² – b² – c²=2bc/3
Determina el valor de: Tg(A/2)
a) 1
b) √2
c) 3
d) 2
e) √2/2
Rpta. : "B"
PREGUNTA 6 :
En un triángulo ABC se cumple que:
3(a+c)(a–c) = b(2c+3b)
Calcular el valor de CosA
a) 1
b) –1/3
c) 1/3
d) 1/2
e) –1/2
Rpta. : "B"
PREGUNTA 7 :
Las medidas de los lados de un triángulo están expresados por tres números consecutivos. Si el valor de la tangente de la mitad del menor ángulo es 1/2. Determinar el valor del Coseno del mayor ángulo.
a) 3/5
b) 4/5
c) 5/13
d) 12/13
e) 13/14
Rpta. : "C"
PREGUNTA 8 :
Si el Coseno del mayor ángulo agudo de un triángulo de lados enteros consecutivos es 1/5. Hallar el perímetro de dicho triángulo.
a) 12
b) 14
c) 16
d) 18
e) 20
Rpta. : "D"
PREGUNTA 9 :
Resuelve el triángulo ABC, si
a = √3
b² + c² = 5
A = 60°
a) 45°,65°,1 y 2
b) 30°,90°,1 y 2
c) 15°,105°,2 y 3
d) 45°,75°,2 y6
e) 30°,90°,3 y 2
Rpta. : "B"
PREGUNTA 10 :
En un triángulo ABC, reduce:
M = bcCos²(A/2)+acCos²(B/2)+abCos²(C/2)
a) p
b) 2p
c) 2p²
d) p²
e) p²/2
Rpta. : "D"
PREGUNTA 11 :
En un triángulo ABC se cumple:
a² = b² + c² – (2/3)bc
Calcula TgA
a) 1/3
b) 3
c) 2√2
d) 2/3
e) 3/2
Rpta. : "C"
PREGUNTA 12 :
En un triángulo reduce:
abcSenA(CtgB +CtgC)
a) a³
b) b³
c) c³
d) abc
e) 3abc
Rpta. : "A"
PREGUNTA 13 :
Los catetos de un triángulo ABC miden AB = 3 ; BC =√7. Si giramos un triángulo de 60° alrededor de BC, halla el coseno del ángulo que se forma la primera y la nueva posición de la hipotenusa AC.
a) 21/25
b) 23/32
c) 25/32
d) 27/32
e) 18/25
Rpta. : "B"
PREGUNTA 14 :
Dado un triángulo ABC, a que es igual:
(p=semiperímetro)
E=(b+c)CosA+(a+c)CosB+(a+b)CosC
a) p
b) 2p
c) 2
d) 0,5
e) 1
Rpta. : "B"
PREGUNTA 15 :
Si el perímetro del triángulo ABC es 24 y el circunradio mide 5.
Halla: SenA + SenB + SenC
a) 1,2
b) 2,4
c) 2,8
d) 2,6
e) 1,8
Rpta. : "B"
PROBLEMAS RESUELTOS
PREGUNTA 1 :
Del gráfico, determina “x”.
A) √11
B) √13
C) √17
D) √19
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 2 :
Del gráfico, determine el Senx
A)√6/6
B)√6/5
C)√6/4
D)√6/3
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 3 :
En el siguiente gráfico se sabe que x² =a+b√2
Calcule E=a − b.
A) 90
B) 91
C) 92
D) 93
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 4 :
En un triángulo dos de sus lados miden 3cm y 4cm y el ángulo comprendido entre ellos mide θ. si: Cosθ=–11/24 , calcular el perímetro del triángulo.
A) 9
B) 11
C) 13
D) 15
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 5 :
En la figura, PQ= 10 m. Halle AB.
A) 10√3 cos28° m
B) 10√3 cos24° m
C) 10√3 sen32° m
D) 10√3 cos26° m
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 6 :
En un triángulo ABC, de lados 3 y 4 unidades, el coseno del ángulo que forman dichos lados es – 11/24. Calcule el perímetro de dicho triángulo.
A) 10
B) 13
C) 15
D) 17
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 7 :
Las medidas de los lados de un triángulo son proporcionales a 6 ; 10 y 14. Si el menor ángulo interno es θ, determine el valor de 13tgθ.
A) 13√3
B) 3
C) 2√3
D) 3√3
E) 4√3
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 8 :
Si en un triángulo ABC de perímetro 10 cm, se cumple que:
Hallar la medida del exradio, relativo al lado “a”.
A) 7 cm
B) 6 cm
C) 8 cm
D) 4 cm
E) 5 cm
RESOLUCIÓN :
Rpta. : "E"
