RAZONES Y PROPORCIONES EJERCICIOS RESUELTOS DE NIVEL BÁSICO E INTERMEDIO PDF
Al finalizar del capítulo el estudiante estará en condiciones de :
► saber comparar cantidad homogéneas o heterogéneas mediante la sustracción o división .
► Aplicar en forma adecuada y efectiva las diversas propiedades de las razones geométricas iguales.
► Resolver en forma razonada, problemas de proporciones, que son básicos para el estudio de la proporcionalidad .
► Reconocer las características inherentes de los objetos dada la comparación para analizar cuantitativamente dichas características .
► Identificar las magnitudes de nuestros entorno y medir su intensidad para representar mediante cantidades (valores) .
► Obtenidas las comparaciones, poder formar proporciones y series de razones geométricas equivalentes induciendo así mismo sus diversas propiedades vinculadas con dicha comparación.
► Deducir , interpretar y manera adecuadamente los resultados obtenidos en la comparación para obtener formas prácticas de resolver problemas de la vida cotidiana y en otras disciplinas.
RESUMEN :
► Una razón aritmética es la comparación de dos términos mediante el establecimiento de una diferencia.
► Una razón geométrica es la comparación de dos términos mediante , el establecimiento de un cociente.
► En toda serie de razones geométricas equivalentes la suma de los antecedentes dividida entre la suma de los consecuentes mantiene inalterable la constante de proporcionalidad.
► En una proporción aritmética la suma de los términos extremos es numéricamente igual a la suma de los términos medios.
► En una proporción geométrica el producto de los extremos es numéricamente igual al producto de los términos extremos.
*
*
*
*
*
*
*
GUIA DE EJERCICIOS PARA LA CLASE
PREGUNTA 1 :
La razón de 2 números es 5/6; el menor es 20. el mayor es:
A) 25
B) 24
C) 30
PREGUNTA 2 :
En un salón hay 45 alumnos de los cuales 24 son varones. ¿Cuál es la razón entre el número de varones y el número de mujeres?
A) 8/9
B) 8/7
C) 7/8
D) 9/8
PREGUNTA 3 :
El mayor de dos números es 42 y la relación entre ambos es de 5 a 7. El menor es:
A) 20
B) 30
C) 40
D) 35
PREGUNTA 4 :
El consecuente de una razón geométrica es 6. Si sumamos 6 a ambos términos de la razón, la nueva razón es igual a la anterior más 1/3. Entonces el antecedente de dicha razón es:
A) –2
B) 4
C) 6
D) 8
PREGUNTA 5 :
Dos números están en razón de 5 a 4. Si los números suman 189, entonces son:
A) 104; 85
B) 105; 84
C) 95; 94
D) 86; 103
PREGUNTA 6 :
Dos números están en razón de 9 a 4. Si su diferencias es 15, los números son:
A) 25 y 10
B) 28 y 13
C) 27 y 12
D) 30 y 15
PREGUNTA 7 :
María y Claudia tienen 24 y 18 amigos, ¿cuántos amigos más, debería tener Claudia para que por cada 8 amigos que tiene María, Claudia tenga 11 amigos?
A) 16
B) 20
C) 18
D) 15
E) 21
PREGUNTA 8 :
En un recipiente que contiene 120 litros de agua y aceite; 30 litros son agua y el resto aceite; ¿cuál es la razón geométrica entre el aceite y el agua?
A) 3
B) 1/5
C) 1/2
D) 4
E) 7
PREGUNTA 9 :
La edad de Manuel es la edad de Carlita como 7 es a 6. Si Manuel tiene 28 años. ¿Cuánto suman sus edades?
A) 56
B) 49
C) 48
D) 50
E) 52
PREGUNTA 10 :
Las edades de 3 hermanos están en la relación de 5; 7 y 3, Si la diferencia entre el mayor y el menor es 12. Determinar la edad del otro hermano.
A) 18
B) 15
C) 27
D) 19
E) 20
PREGUNTA 11 :
Se tiene 3 números proporcionales a 4 ; 5 y 3 la diferencia entre el mayor y el menor es 222. Hallar el número que no es mayor ni menor
A) 333
B) 528
C) 509
D) 444
E) 324
PREGUNTA 12 :
La suma, diferencia y producto de 2 números están en la relación de 5 ; 1 y 36. Determinar el mayor de dichos números.
A) 24
B) 100
C) 18
D) 80
E) 21
PREGUNTA 13 :
Las edades de tres hermanos están en la relación de los números 4; 9 y 7, si dentro de 8 años las tres edades sumarán 84. Determinar la edad del mayor.
A) 17
B) 19
C) 27
D) 21
E) 24
PREGUNTA 14 :
En una granja por cada 5 vacas hay 7 pollos, y por cada 3 pollos hay 4 corderos, si se cuentan 320 cabezas ¿cuántas vacas hay?
A) 200
B) 105
C) 140
D) 75
E) 115
PREGUNTA 15 :
El producto de los términos de una proporción geométrica discreta es 441. Determinar su suma.
A) 32
B) 28
C) 35
D) 36
E) 40
PREGUNTA 16 :
Miriam, Jesús y Patty tienen cantidades de dinero proporcionales a 18 ; 13 y 12. Si Miriam le da a Patty 180 soles, entonces tendrían las dos la misma cantidad de dinero. ¿Cuánto tienen entre las 3?
A) 4500
B) 1290
C) 1800
D) 1400
E) 1590
PREGUNTA 17 :
Las edades de Patty, Teresa y Juan están en la relación de 24; 5 y 3. Si dentro de 6 años sus edades sumaran 66. Determinar la edad del menor
A) 18
B) 12
C) 20
D) 32
E) 14
PREGUNTA 18 :
Se tiene 4 números proporcionales a 3; 5; 7 y 9; si la suma de los dos menores es 200. Determinar la diferencia de los 2 mayores.
A) 200
B) 400
C) 50
D) 25
E) 60
PREGUNTA 19 :
En un cofre hay 10 monedas de oro y 35 monedas de plata. ¿Cuántas monedas de oro hay que aumentar para que la relación sea de 5 a 7?
A) 15
B) 6
C) 7
D) 8
E) 12
PREGUNTA 20 :
En una reunión hay 90 personas, por cada 2 hombres ingresaron 3 mujeres. Luego de 5 horas se retiran 10 mujeres. ¿Cuál es la nueva relación entre hombres y mujeres?
A) 9/7
B) 5/9
C) 9/11
D) 3/7
E) 4/9
PREGUNTA 21 :
María y Ricardo se encuentran en la Av. La Marina separados por 30 cuadras, si por cada 2 cuadras que avanza María, Ricardo avanza 3 cuadras y ambos van a encontrarse, ¿cuántas cuadras recorre Ricardo?
A) 12
B) 16
C) 18
D) 15
E) 14
PREGUNTA 22 :
La edad de Ana y de Juan están en la relación de 4 a 7. Si dentro de 6 años sus edades sumaran 56 años. Hallar la edad de Ana.
A) 40
B) 18
C)24
D) 16
E) 21
PREGUNTA 23 :
Se tiene una mezcla de 2 líquidos A y B, donde el volumen del líquido A es los 3/5 del volumen del líquido B, además la mezcla tiene 64 litros. ¿Cuántos litros del líquido B se deberán agregar para que por cada 12 litros de A haya 25 litros de B?
A) 10
B) 24
C) 40
D) 18
E) 28
PREGUNTA 24 :
En una fiesta hay 80 personas, además por cada 7 varones hay 9 mujeres, ¿cuántos varones deben llegar a la fiesta para que las cantidades de varones y mujeres sean iguales?
A) 15
B) 28
C) 10
D) 17
E) 20
PREGUNTA 25 :
En una conferencia se reúnen 480 doctores, donde por cada 5 varones hay una mujer, ¿cuántas doctoras deben llegar a dicha conferencia para que por cada 5 doctores haya 3 mujeres?
A) 40
B) 160
C) 200
D) 180
E) 45
PREGUNTA 26 :
Del recipiente II se retira cierto volumen y se deposita en I, con la condición que en dicho recipiente por cada 2 litros de agua se tenga 1 litro de vino. ¿Cuántos litros quedaron en el recipiente II?
A) 100
B) 200
C) 20
D) 180
E) 120
PREGUNTA 27 :
En una granja se crían pollos y conejos, los cuales están en la relación de 9 a 7, si se cuentan 460 patas, ¿cuánto dinero se obtendrá si se venden la tercera parte de los pollos y la quinta parte de los conejos, si sus precios unitarios son 12 y 20 soles?
A) 640
B) 800
C) 300
D) 900
E) 1200
PREGUNTA 28 :
Se tiene una solución de agua y vino de 280 litros, si por cada 9 litros de vino hay 5 litros de agua; ¿cuál es el volumen de agua?
A)100 L
B)300 L
C)200 L
D) 180 L
E) 50 L
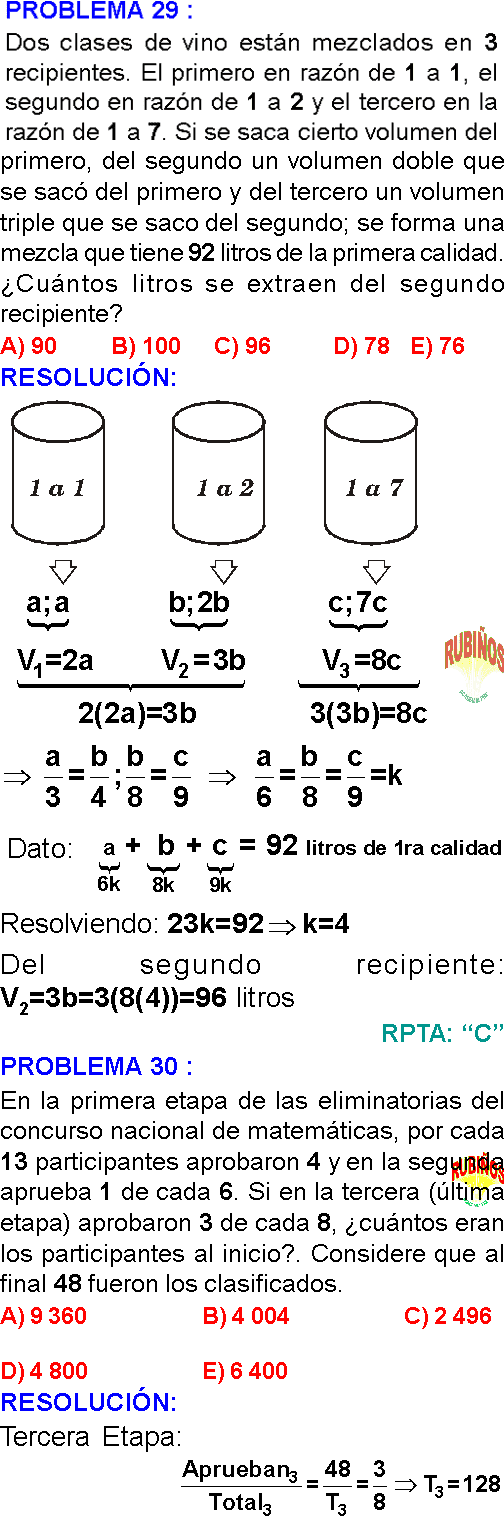
PREGUNTA 29 :
La suma y la diferencia de 2 números están en la relación de 7 a 3. Si la suma de sus cuadrados es 464. Hallar el mayor de dichos números.
A) 20
B) 8
C) 16
D) 30
E) 10
PREGUNTA 30 :
Se tiene una mezcla de agua y vino de 120 litros, si por cada 5 litros de agua hay 19 litros de vino, ¿cuál es el volumen de vino?
A) 95 L
B) 100 L
C) 25 L
D) 40 L
E) 35 L
PREGUNTA 31 :
La suma y la diferencia de 2 números están en la relación de 9 a 3. si la diferencia de sus cuadrados es 243. Hallar el menor.
A) 11
B) 18
C) 7
D) 5
E) 9
PREGUNTA 32 :
Las edades de Ana y Rosa están en la razón de 3 a 2. Si la suma de sus edades es 80 años, ¿cuántos años más tiene la mayor?
A) 32
B) 16
C) 24
D) 48
PREGUNTA 33 :
La razón entre el perímetro de A y el de B es de 3 a 8. Si el perímetro de A es 69 m, ¿cuántos metros tiene el perímetro B?
A) 148
B) 178
C) 126
D) 184
PROBLEMAS PROPUESTOS CON RESPUESTAS
PREGUNTA 1 :
La razón aritmética de dos números es 12. si uno de ellos es el cuádruple del otro, hallar la suma de dichos números.
A) 18
B) 20
C) 24
D) 30
E) 32
PREGUNTA 2 :
La razón entre 2 números es 3/5. Determinar la diferencia entre ellos, sabiendo que su suma es 72.
A) 9
B) 12
C) 16
D) 18
E) 24
PREGUNTA 3 :
Dos números están en la razón de 3 es a 2. Si la suma de dichos números excede a la diferencia de los mismos en 80, hallar el mayor de los números.
A) 45
B) 60
C) 75
D) 90
E)120
PREGUNTA 4 :
A una fiesta asistieron 140 personas entre hombres y mujeres. Por cada 3 mujeres hay 4 hombres. Si se retiran 20 parejas. ¿Cuál es la razón entre el número de mujeres y el número de hombres que se quedan en la fiesta?
A) 2/3
B) 4/5
C) 1/3
D) 3/4
E) 5/3
PREGUNTA 5 :
Sabiendo que la razón geométrica de dos números cuya diferencia de cuadrados es 180, se invierte al sumar 6 al menor y restar 6 al mayor. Hallar su producto.
A) 180
B) 216
C) 270
D) 396
E) Hay dos respuestas
PREGUNTA 6 :
Si m es la media proporcional de 9 y 4; n es la cuarta proporcional de 8, m y 12. Hallar: m + n
A) 12
B) 15
C) 18
D) 20
E) 24
PREGUNTA 7 :
José y Juan tienen S/.700 entre ambos, lo que tiene José es a lo que tiene Juan como 4 es a 3. ¿Cuánto tiene José?
A) S/.400
B) S/.300
C) S/.1000
D) S/.100
E) S/.600
PREGUNTA 8 :
En un salón hay 40 varones y 30 mujeres. ¿Cuántas parejas deben retirarse para que los varones que quedan sean a las mujeres que quedan como 7 es a 5?
A) 4
B) 5
C) 6
D) 8
E) 10
PREGUNTA 9 :
El jardinero A planta rosas más rápidamente que el jardinero B en la proporción de 4 a 3. Cuando B planta x rosas en 1 hora, A planta x+2 rosas. ¿Cuántas rosas planta B en 4 horas?
A) 6
B) 8
C) 32
D) 24
E) 12
PREGUNTA 10 :
Si: a/3=b/5 =c/7, además 2a+b+c=54, calcular: E= a+ 2b+ c
A) 60
B) 64
C) 70
D) 72
E) 80
PREGUNTA 11 :
Los ángulos de un triángulo son entre sí como los números 4 ; 7 y 9. Hallar el menor de los ángulos.
A) 20°
B) 24°
C) 28°
D) 32°
E)36°
PREGUNTA 12 :
En una serie de 3 razones geométricas equivalentes y continuas, el primer antecedente es 64 veces el último consecuente. Hallar el valor de la constante de proporcionalidad.
A) 1
B) 2
C) 4
D) 8
E) 16
PREGUNTA 13 :
La suma, la diferencia y el producto de dos números están en la misma relación que los números 4, 2 y 15. ¿Cuál es el mayor de los números?
A) 4
B) 10
C) 14
D) 15
E) 16
PREGUNTA 14 :
Los antecedentes de varias razones geométricas iguales son: 2; 3; 4 y 5; el producto del primer antecedente y los 3 últimos consecuentes es 41160. La suma de los consecuentes es:
A) 94
B) 98
C) 95
D) 96
E) 97
PREGUNTA 15 :
En una serie de 4 razones geométricas continuas equivalentes se cumple que la suma de los antecedentes con el doble de la suma de los dos primeros consecuentes es 1500. Calcular la suma de los dos primeros antecedentes sabiendo que la constante de proporcionalidad es un número entero.
A) 880
B) 900
C) 920
D) 949
E) 960
PREGUNTA 16 :
En cierto campeonato un equipo de fútbol, de los 18 partidos que jugó, ganó 4 más de los que empató, y el número de partidos que ganó es a los que perdió como 4 a 3. ¿Cuántos partidos empató?
A) 2
B) 3
C) 4
D) 5
E) 6
PREGUNTA 17 :
La razón aritmética de dos números es 20 y su razón geométrica es 2. El número mayor es:
A) 20
B) 30
C) 40
D) 60
E) 80
PREGUNTA 18 :
La razón geométrica entre la suma y la diferencia de dos números es 5/3. Si la suma del mayor con el triple del menor es 14, hallar la suma de los cuadrados de los números.
A) 68
B) 72
C) 76
D) 80
E)100
PREGUNTA 19 :
En una proporción geométrica continua la suma de los 4 términos es 64 y la diferencia entre los extremos 48. Hallar la suma de los extremos.
A) 49
B) 72
C) 50
D) 85
E) 63
PREGUNTA 20 :
En un momento de una fiesta, el número de hombres que no bailan es al número de personas que están bailando como 1 es a 6. Además el número de damas que no bailan es al número de hombres como 3 es a 20. Encontrar el número de damas que están bailando si en total asistieron 456 personas.
A) 120
B) 150
C) 180
D) 200
E) 210
CLAVES – RESPUESTAS : 1)B 2)D 3)B 4)A 5)B 6)B 7)A 8)B 9)D 10)A 11)E 12)C 13)D 14)B 15)E 16)E 17)C 18)A 19)C 20)C