TEORÍA DE PROBABILIDAD EJERCICIOS RESUELTOS PDF RAZONAMIENTO MATEMÁTICO–ARITMÉTICA
CÁLCULO DE PROBABILIDADES
La Teoría de Probabilidad tiene como objetivo el estudio de las leyes que gobiernan a los fenómenos aleatorios, es decir, trata con las propiedades de los fenómenos aleatorios que dependen esencialmente de la noción de aleatoriedad y no de otros aspectos del fenómeno considerado.
OBJETIVOS DEL APRENDIZAJE :
☛ Conocer conceptos tales como experimento aleatorio y espacio muestral.
☛ Estudiar la definición clásica de probabilidad.
☛ Conocer algunas propiedades de probabilidad.
☛ Estudiar la probabilidad condicional.
☛ Entender la probabilidad de eventos independientes.
CONCEPTOS PREVIOS
EXPERIMENTO ALEATORIO (𝛆)
Es toda prueba o ensayo que al realizarse en las mismas condiciones su resultado no se puede predecir, es decir, el resultado depende del azar.
ESPACIO MUESTRAL (𝛀)
Es el conjunto de todos los posibles resultados que se pueden obtener al realizar el experimento.
EVENTO
Es cualquier subconjunto del espacio muestral. Se denota utilizando las letras mayúsculas del abecedario (A, B, C, …)
EVENTOS PARTICULARES
EVENTO IMPOSIBLE
Es aquel evento que carece de elementos.
EVENTO UNITARIO
Llamado también evento elemental, es aquel evento que solo tiene un elemento.
EVENTO SEGURO
Es aquel evento cuyos elementos son todos los elementos del espacio muestral.
EVENTO CONTRARIO
Dado un evento “M”; el evento contrario es aquel que posee los elementos que no posee “M” y se le designa M'.
OPERACIONES CON EVENTOS
Dado que los eventos son conjuntos, también se pueden hacer operaciones entre ellos.
EVENTOS MUTUAMENTE EXCLUYENTES
Sean A y B dos eventos de un cierto experimento aleatorio; se dice que estos eventos son mutuamente excluyentes si no pueden ocurrir a la vez
DEFINICIÓN CLÁSICA DE PROBABILIDAD
Dado un espacio muestral (Ω) finito; en el cual todos sus elementos tienen la misma posibilidad de ocurrir; la probabilidad de que ocurra un evento A (A ⊂ Ω); se denota como P(A).
PROBABILIDAD CONDICIONAL
Definiremos esta probabilidad cuando exista un evento “A”, que ocurre, condicionado a que haya ocurrido previamente otro evento “B” y lo denotaremos P(A/B) .
EVENTOS INDEPENDIENTES
Dos eventos son independientes si la ocurrencia de uno de ellos no tiene efecto en la probabilidad de ocurrencia del otro. En caso contrario se dirá que son dependientes.
Ejemplo :
Al lanzar dos veces una misma moneda, los eventos que se obtienen son eventos independientes, porque el resultado que se obtiene en el primer lanzamiento (1er evento), no afecta o no influye en el resultado que se obtenga en el segundo lanzamiento (2do lanzamiento).
PROBLEMAS RESUELTOS
PREGUNTA 1 :
Al lanzar una moneda cuatro veces consecutivas, ¿cuál es la probabilidad de obtener tres sellos?
A) 1/8
B) 1/16
C) 1/4
D) 1/64
E) 1/32
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 2 :
PREGUNTA 3 :
La probabilidad de realizar el siguiente suceso: “Obtener cara a lo más dos veces al lanzar al aire tres veces una moneda” es:
A) 1/2
B) 3/4
C) 7/8
D) 3/8
E) 1/4
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 4 :
Con cinco ingenieros y cuatro médicos se desea formar un comité de seis miembros. ¿Cuál es la probabilidad de que dicho comité incluya, a lo más, tres ingenieros?
A) 13/42
B) 14/33
C) 20/33
D) 25/42
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 28 :
En un estante de la biblioteca del área de Sociales, se va a ordenar en una fila 5 libros distintos de Adry, 4 libros distintos de Terry y 3 libros distintos de Salette. ¿Cuál es la probabilidad que los libros de Terry se encuentren juntos?
A) 1/55
B) 1/27
C) 3/55
D) 3/64
E) 4/27
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 5 :
En la sala de pediatría de un hospital el 70% de los pacientes son varones, de estos el 42% son menores de 3 años, y el 30% de las niñas son menores de 3 años. Una pediatra que ingresa a la sala selecciona un infante al azar. ¿Cuál es la probabilidad de que este tenga 3 o más años?
A) 0,484
B) 0,616
C) 0,294
D) 0,285
E) 0,304
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 6 :
Tres jugadores A, B y C extraen (en ese orden) una carta con reposición de una baraja de 52 cartas. El primero que obtiene corazón gana. Calcule la probabilidad que gane A.
A) 9/74
B) 18/37
C) 16/37
D) 2/37
E) 8/37
RESOLUCIÓN :
Rpta. : "C"
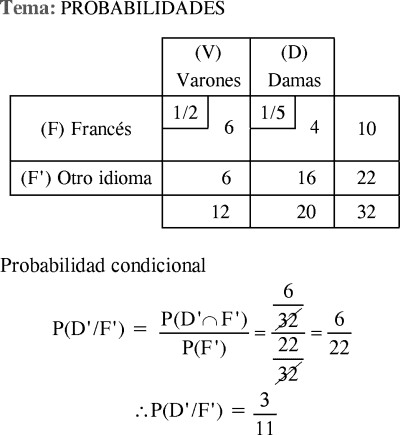
PREGUNTA 7 :
Una clase está formada por 12 varones y 20 damas; la mitad de los varones y la quinta parte de las damas han elegido Francés como asignatura de verano. Si de las 32 personas se escoge una persona al azar y resulta que no eligió Francés como asignatura de verano, ¿cuál es la probabilidad de que no sea una dama?
A) 10/11
B) 1/2
C) 3/11
D) 3/5
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 8 :
En una reunión de 30 profesionales entre médicos y odontólogos: 22 son hombres, 14 son odontólogos y 2 son médicos y mujeres. Para cierta tarea se eligen al azar y, a la vez, a 5 profesionales. Si las personas elegidas resultan ser mujeres, halle la probabilidad de que sean odontólogas.
A) 5/16
B) 7/32
C) 3/28
D) 3/36
E) 6/14
RESOLUCIÓN :
Rpta. : "C"
PROBLEMAS PROPUESTOS
PREGUNTA 1 :
Se tiene un lote de 10 vacunas contra la COVID - 19, de las cuales 3 son defectuosas. Si se elige al azar 2 vacunas, ¿cuál es la probabilidad de obtener una defectuosa y una no defectuosa?
A) 7/15
B) 8/15
C) 7/20
D) 11/20
Rpta. : "A"
PREGUNTA 2 :
Se lanzan simultáneamente 5 monedas al aire. ¿Cuál es la probabilidad de obtener 3 caras y 2 sellos?
A) 7/16
B) 5/16
C) 3/8
D) 5/8
Rpta. : "B"
PREGUNTA 3 :
Una pareja de esposos con 4 hijos se van al cine y encuentran una fila de 6 asientos. Calcule la probabilidad de que puedan ubicarse si los esposos siempre deben estar juntos.
A) 5/9
B) 2/3
C) 1/9
D) 1/3
Rpta. : "D"
PREGUNTA 4 :
Cinco amigos, 3 varones y 2 mujeres, se van al cine y encuentran una fila libre con cinco asientos. Si ellos eligen al azar sus asientos, ¿cuál es la probabilidad de que los varones y las mujeres queden en forma alternada?
A) 3/5
B) 1/10
C) 3/8
D) 5/8
Rpta. : "B"
PREGUNTA 5 :
Elena observa en el Senami que la probabilidad que llueva mañana en el Cusco es de 0,60; la probabilidad de que truene es de 0,30; y la probabilidad de que llueva y truene es de 0,10. Calcule la probabilidad de que no llueva ni truene.
A) 0,2
B) 0,5
C) 0,8
D) 0,3
Rpta. : "A"
PREGUNTA 6 :
Se escoge aleatoriamente un número de 15 cifras que sumen 133. Señale la probabilidad que resulte un número capicúa.
A) 5/8
B) 3/15
C) 1/9
D) 1/15
Rpta. : "D"
PREGUNTA 7 :
Tres clientes dejan sus sombreros en el guardarropa al llegar a un restaurante y estos sombreros le son devueltos aleatoriamente cuando se retiran del lugar. ¿Cuál es la probabilidad de que ningún cliente reciba su propio sombrero?
A) 1/3
B) 1/6
C) 1/4
D) 5/12
Rpta. : "A"
PREGUNTA 8 :
Se lanzan dos dados y se suman los resultados de sus caras superiores. Si se obtienen una suma mayor a 6, ¿cuál es la probabilidad de obtener una suma igual a 7?
A) 2/7
B) 1/8
C) 5/12
D) 3/8
Rpta. : "A"
PREGUNTA 9 :
Una alarma de seguridad tiene instalados dos indicadores. Ante una emergencia los indicadores se activan de forma independiente. La probabilidad de que se active el primer indicador es 0,95 y de que se active el segundo es 0,90. Halle la probabilidad que ante una emergencia se active solo uno de los indicadores.
A) 0,25
B) 0,17
C) 0,14
D) 0,35
Rpta. : "C"
PREGUNTA 10 :
En una urna se tienen esferas numeradas del 1 al 13, y se extrae una esfera al azar. Determine la probabilidad de que esta sea mayor a 8 si se sabe que la bola extraída es par.
A) 1/4
B) 3/4
C) 1/3
D) 2/5
Rpta. : "C"
PREGUNTA 11 :
Martín y José practican básquetbol. Martín encesta 2 de cada 5 lanzamientos y José 3 de cada 7. Si ambos lanzan a la canasta una sola vez y los dos eventos son independientes, ¿cuál es la probabilidad de que al menos uno de ellos enceste?
A) 23/35
B) 6/35
C) 5/12
D) 5/7
Rpta. : "A"
PREGUNTA 12 :
Sean A y B eventos independientes asociados a un experimento aleatorio. Se sabe que la probabilidad de que A o B ocurra es igual a 0,6; mientras que la probabilidad de que A ocurra es igual a 0,4. Determine la probabilidad de que ocurra B.
A) 1/2
B) 1/3
C) 1/4
D) 1/5
Rpta. : "B"
PREGUNTA 13 :
Un microbús tiene solo cuatro pasajeros cuando le faltan cinco paraderos para el final de la ruta. Si todos los pasajeros tienen la misma probabilidad de bajarse en cualquier paradero, ¿cuál es la probabilidad de que baje solo uno de los pasajeros en cada uno de los cuatro últimos paraderos?
A) 16/125
B) 16/125
C) 24/625
D) 1/125
Rpta. : "C"
PREGUNTA 14 :
Las probabilidades que tienen Arturo y Brenda de resolver un mismo problema son 1/3 y 2/5, respectivamente. Si ambos intentan resolverlo, calcule la probabilidad de que el problema sea resuelto si son eventos independientes.
A) 1/5
B) 1/4
C) 2/5
D) 3/5
Rpta. : "D"
PREGUNTA 15 :
Se tiene que enviar tres cartas diferentes con sus respectivos sobres a tres destinatarios diferentes. Si se introducen las tres cartas en los tres sobres vacíos aleatoriamente, ¿cuál es la probabilidad de que por lo menos una de las cartas sea introducida en el sobre que le corresponde? .
A) 5/12
B) 1/3
C) 1/4
D) 2/3
Rpta. : "D"
PREGUNTA 16 :
En el cumpleaños de Beto, en un determinado momento, se observa que 30 mujeres están bailando. Si asistieron 50 varones y 40 mujeres, y se escoge una persona al azar, determine
n: probabilidad de que sea varón, dado que está bailando.
m: probabilidad de que no baile, dado que es mujer.
A) 1/2 ; 1/4
B) 1/3 ; 1/4
C) 1/2 ; 1/8
D) 1/5 ; 1/4
Rpta. : "A"
PREGUNTA 17 :
Por la mañana, ingresaron a un taller tres automóviles con problemas eléctricos, ocho con problemas mecánicos y tres con problemas de chapa, y por la tarde dos con problemas eléctricos, tres con problemas mecánicos y uno con problema de chapa. ¿Cuál es la probabilidad de que un automóvil con problemas eléctricos haya acudido por la mañana?
A) 1/3
B) 3/5
C) 3/4
D) /11
Rpta. : "B"
PREGUNTA 18 :
En un club deportivo, el 52% de los socios son hombres. Entre los socios, el 35% de los hombres practica natación, así como el 60% de las mujeres. Si se elige un socio al azar, ¿cuál es la probabilidad de que practique natación?
A) 0,48
B) 0,47
C) 0,95
D) 0,182
Rpta. : "B"
PREGUNTA 19 :
Un grupo de estudiantes rinden cada uno el examen del curso de Ecuaciones Diferenciales y el examen del curso de Dibujo Lineal en un mismo día, pero en diferentes horarios. La probabilidad de que un estudiante apruebe el examen de Ecuaciones Diferenciales es 0,6 y de que apruebe ambos exámenes es de 0,5. Si un estudiante elegido al azar aprobó el examen de Ecuaciones Diferenciales, ¿cuál es la probabilidad de que apruebe el examen de Dibujo Lineal?
A) 5/6
B) 5/8
C) 3/4
D) 5/9
Rpta. : "A"
PREGUNTA 20 :
El egresado César recibió un balotario con 50 temas para presentarse al examen de Suficiencia Profesional y optar el título profesional de Ingeniero. El jurado elige al azar dos temas y César debe responder correctamente uno de los dos para aprobar el examen. Si César sabe solo 35 temas, ¿cuál es la probabilidad de que apruebe el examen?
A) 17/35
B) 3/7
C) 32/35
D) 7/10
Rpta. : "C"
SEGUNDA GUIA DE PROBLEMAS
PREGUNTA 1 :
Un sistema detector de humo usa dos dispositivos Ay B. Si el humo está presente, la probabilidad de que sea detectado por el dispositivo A es 0,95; por el dispositivo B, 0,98; y por ambos dispositivos, 0,94. Si hay humo, halle la probabilidad de que no sea detectado.
A) 0,99
B) 0,04
C) 0,01
D) 0,05
E) 0,44
Rpta. : "C"
PREGUNTA 2 :
Para un estudio de cultura general se encuestó a 200 estudiantes encontrándose que 10 de ellos habían leído “Paco Yunque” de César Vallejo; 12 habían leído “Mi planta de naranja lima” de Vasconcelos” y 181 no habían leído ninguna de estas obras. ¿Cuál es la probabilidad de que un estudiante seleccionado al azar no haya leído “Paco Yunque” dado que no leyó “Mi planta de naranja lima”?
A) 3/200
B) 12/17
C) 90/97
D) 45/47
E) 181/188
Rpta. : "E"
PREGUNTA 3 :
En un almacén hay 6 latas de duraznos en conserva, 2 de ciruelas y 4 de piñas. ¿Cuál es la probabilidad de que al elegir 3 latas al azar resulten de la misma fruta?
A) 25/36
B) 2/13
C) 3/92
D) 24/455
E) 6/55
Rpta. : "E"
PREGUNTA 4 :
La aprobación de una propuesta de concesión depende de los revisores. Un grupo de expertos evaluó un conjunto de proyectos de investigación en cuanto a si valía la pena financiarlos. Cuando estos mismos proyectos se sometieron a un segundo grupo independiente, la decisión de proporcionar fondos se revirtió en 30% de los casos. Si la probabilidad de que un proyecto sea considerado apto para el financiamiento por el primer grupo de revisión es 0,2, ¿cuál es la probabilidad de que solamente un grupo de expertos apruebe el proyecto?
A) 0,18
B) 0,24
C) 0,27
D) 0,30
E) 0,42
Rpta. : "D"
PREGUNTA 5 :
La profesora Delia desea programar una reunión con cada uno de sus ocho asistentes, cuatro hombres y cuatro mujeres, para coordinar el curso de Muestreo. ¿Cuál es la probabilidad de que por lo menos una mujer asistente se encuentre entre los primeros tres con quienes la profesora se reúna?
A) 13/14
B) 3/4
C) 6/7
D) 27/28
E) 51/56
Rpta. : "A"
PREGUNTA 6 :
La probabilidad que tiene Rafael de ganar a José Luis en una partida de ajedrez es 3/5. Si no hay empates, ¿cuál es la probabilidad que tiene Rafael de ganar por lo menos una de tres partidas? Asuma independencia.
A) 111/125
B) 4/125
C) 117/125
D) 1/125
E) 97/125
Rpta. : "C"
PREGUNTA 7 :
El gerente de un servicio privado de mensajería está preocupado por la posibilidad de una huelga por parte de algunos empleados. Sabe que la probabilidad de una huelga de pilotos es de 0,75 y la probabilidad de una huelga de choferes es 0,65. Más aún, sabe que si los choferes hacen una huelga, existe una posibilidad de 90% de que los pilotos apoyen la huelga. Si los pilotos hacen huelga, ¿cuál es la probabilidad de que los choferes apoyen la huelga?
A) 13/15
B) 56/75
C) 39/50
D) 34/53
E) 72/95
Rpta. : "C"
PREGUNTA 8 :
Un nuevo secretario ha recibido 7 contraseñas de computadora, solo una de ellas permitirá el acceso a un archivo de computadora. Como el secretario no tiene idea de cuál de las contraseñas es la correcta, selecciona una de ellas al azar y la prueba. Si es incorrecta, la desecha y selecciona otra al azar de entre las restantes, prosiguiendo así hasta que encuentra la correcta. Si se ha iniciado un sistema de seguridad para que si se prueban 3 contraseñas incorrectas el archivo de computadora queda bloqueado y se niega el acceso, ¿cuál es la probabilidad de que el secretario tenga acceso al archivo?
A) 119/120
B) 1/120
C) 4/7
D) 1/49
E) 3/7
Rpta. : "E"
PREGUNTA 9 :
Los 50 socios de la cooperativa “Rosa de América” decidieron rifar un televisor para lo cual eligieron a 4 de sus socios como organizadores de esta actividad. Si hay 3 premios para ser concedidos y cada socio compra un boleto, ¿cuál es la probabilidad de que los organizadores ganen todos los premios?
A) 47/490
B) 37/245
C) 47/98
D) 69/490
E) 1/4900
Rpta. : "E"
PREGUNTA 10 :
En una ciudad los registros de delitos muestran que 20% son violentos y 80% no son violentos. Se denuncian 90% de delitos violentos y solo 70% de los no violentos. ¿Cuál es la proporción de delitos denunciados en esta ciudad?
A) 28/37
B) 37/50
C) 9/37
D) 14/25
E) 9/50
Rpta. : "B"
PREGUNTA 11 :
De los viajeros que llegan al aeropuerto Jorge Chávez, 60% vuelan en líneas aéreas comerciales y el resto en aviones de propiedad privada. De quienes viajan en líneas aéreas comerciales, 50% viajan por negocios en tanto que 60% de quienes llegan en aviones privados viajan por negocios. Se selecciona al azar una persona que llega a este aeropuerto, ¿cuál es la probabilidad de que la persona viaje por negocios?
A) 0,24
B) 0,54
C) 0,30
D) 0,11
E) 0,44
Rpta. : "B"
PREGUNTA 12 :
Dos inspectores examinan un artículo. Cuando un artículo defectuoso entra a la línea de inspección, la probabilidad de que el primer inspector lo deje pasar es 0,1. De los artículos defectuosos que deja pasar el primer inspector, el segundo dejará pasar 5 de 10. ¿Qué fracción de artículos defectuosos dejan pasar ambos inspectores?
A) 1/5
B) 3/5
C) 1/10
D) 1/20
E) 1/2
Rpta. : "D"
PREGUNTA 13 :
Una compañía petrolera en la actualidad tiene dos proyectos activos, uno en Asia y el otro en Europa. Sea A: “El proyecto asiático tiene éxito” y B: “El proyecto europeo tiene éxito”. A y B son eventos independientes con P(A) = 0,4 y P(B) = 0,7. Dado que por lo menos uno de los dos proyectos tiene éxito, ¿cuál es la probabilidad de que solo el proyecto asiático tenga éxito?
A) 4/27
B) 6/41
C) 2/41
D) 2/11
E) 12/83
Rpta. : "B"
PREGUNTA 14 :
La probabilidad de que Lucho escuche el despertador es de 0,80, y si lo escucha la probabilidad de que llegue a tiempo a su trabajo es de 0,90, y si no escucha el despertador esta probabilidad disminuye a 0,50. Si Lucho llegó a tiempo a su trabajo, ¿cuál es la probabilidad de haber escuchado el despertador?
A) 8/9
B) 36/41
C) 41/50
D) 50/81
E) 25/36
Rpta. : "B"
PREGUNTA 15 :
Los equipos “Deportivo Omas” y “Laraos Querido” juegan una serie de partidos, donde no hay empates, hasta que un equipo gane cuatro de ellos. Los partidos se juegan de manera independientes y la probabilidad de que “Deportivo Omas” gane cualquier juego es 1/4. ¿Cuál es la probabilidad de que la serie dure exactamente 5 partidos?
A) 81/256
B) 21/64
C) 4/11
D) 13/28
E) 2/11
Rpta. : "B"
PREGUNTA 16 :
Se observa que hombres y mujeres reaccionan de modo diferente a un conjunto determinado de circunstancias; se sabe que el 70% de las mujeres reaccionan positivamente a estas circunstancias mientras que de este mismo modo reaccionan solo 40% de los hombres. Un grupo de 20 personas, 15 mujeres y 5 hombres, se sometió a estas circunstancias y a los sujetos se les pidió que describieran sus reacciones en un cuestionario escrito. Una respuesta escogida al azar de las 20 fue negativa. ¿Cuál es la probabilidad de que haya sido de un hombre?
A) 0,5
B) 0,6
C) 0,7
D) 0,4
E) 0,8
Rpta. : "D"