MÁXIMOS Y MÍNIMOS EJERCICIOS RESUELTOS PDF RAZONAMIENTO MATEMÁTICO
MÁXIMOS MÍNIMOS LÓGICOS ALGEBRAICOS GEOMÉTRICOS
Entre los problemas que nos enfrentamos en la vida cotidiana siempre se desea obtener cómo se puede hacer el menor gasto posible de dinero o cómo obtener las mayores ganancias en un proceso comercial.
En las empresas en general siempre es una preocupación el de liderar el mercado para lo cual tratan de obtener los menores precios del mercado, pero también el de dar un producto de alta calidad.
Entre los valores de una función puede haber uno que sea más grande (máximo) o más pequeño (mínimo) que los demás.
En muchísimos problemas prácticos importa saber a que valor de la variable corresponde tal valor de la función.
PREGUNTA 1 :
Cuando Yeni va a comprar al supermercado, observa que en la sección de frutas, por un kilogramo de naranjas se obtienen seis pequeñas o cuatro grandes; además, el precio de un kilogramo de naranjas varía de S/ 4 a S/ 6. Determine el mínimo costo, para que Yari pueda comprar una docena de naranjas grandes y dos docenas de naranjas pequeñas.
A) S/ 27
B) S/ 28
C) S/ 30
D) S/ 20
RESOLUCIÓN :
Mínimo costo por kilogramo: S/ 4
Una docena de naranjas grandes: 3 kg.
Dos docenas de naranjas pequeñas: 4 kg.
Costo mínimo: 4(3) + 4(4) = 28 soles.
Rpta. : "B"
PREGUNTA 2 :
La cantidad de autos vendidos en el último mes del año está dado por la ecuación:
V(x)= x² – 60x+1150
donde x representa el ahorro en miles de soles que todos los clientes han alcanzado en el mes de diciembre.
¿Cuál es el mínimo número de autos que se venderá en este mes?
A) 250
B) 200
C) 400
D) 500
E) 25
RESOLUCIÓN :
La cantidad de autos vendidos está dada por la ecuación:
V(x)= (x² –2×30x + 900) + 250
V(x)= 250 + ( x – 30)²
La venta de autos mínima en el mes de diciembre será de 250.
Rpta. : "A"
PREGUNTA 3 :
Leo es un comerciante que vende arroz al por menor y solo dispone de una gran cantidad de bolsas de plástico, con capacidades de 1, 3 y 6 kg. Si en cada venta debe utilizar los tres tipos de bolsas, ¿cuántas bolsas como mínimo empleará para vender 286 kg de arroz?
A) 49
B) 46
C) 48
D) 38
E) 42
RESOLUCIÓN :
Para emplear la mínima cantidad de bolsas, debe emplear la mayor cantidad de bolsas de 6 kg
Luego 286 = 6 (47) + 4
Luego 1 + 3 + 6(47) = 286
1 bolsa de 1 kg
1 bolsas de 3 kg
47 bolsas de 6 kg, total empleara´ : 47 + 1 + 1 = 49
Rpta. : "A"
PREGUNTA 4 :
Nacho es el padrino de la promoción de inicial del colegio Carrusel, además cuenta con cierta cantidad de dinero para hacerle un regalo a cada uno. Si la cantidad de dinero que destina para el regalo de cada ahijado es tanto como el número que representa la cantidad de ahijados de la promoción, menos 6, y el dinero que tiene no supera a S/ 300, ¿cuál es el mayor número de ahijados que pueden formar dicha promoción?
A) 20
B) 25
C) 18
D) 30
RESOLUCIÓN :
Sea “X” el número de ahijados
Dinero para el regalo de cada uno es: (X – 6)
Cantidad de dinero destinado para los regalos es: X (X – 6) el cual no supera a S/. 300
Con lo cual tenemos: X (X – 6) ≤ 300,
Como “X” representa número de personas entonces tiene un valor entero y el mayor número que cumple es: X = 20
Rpta. : "A"
PREGUNTA 5 :
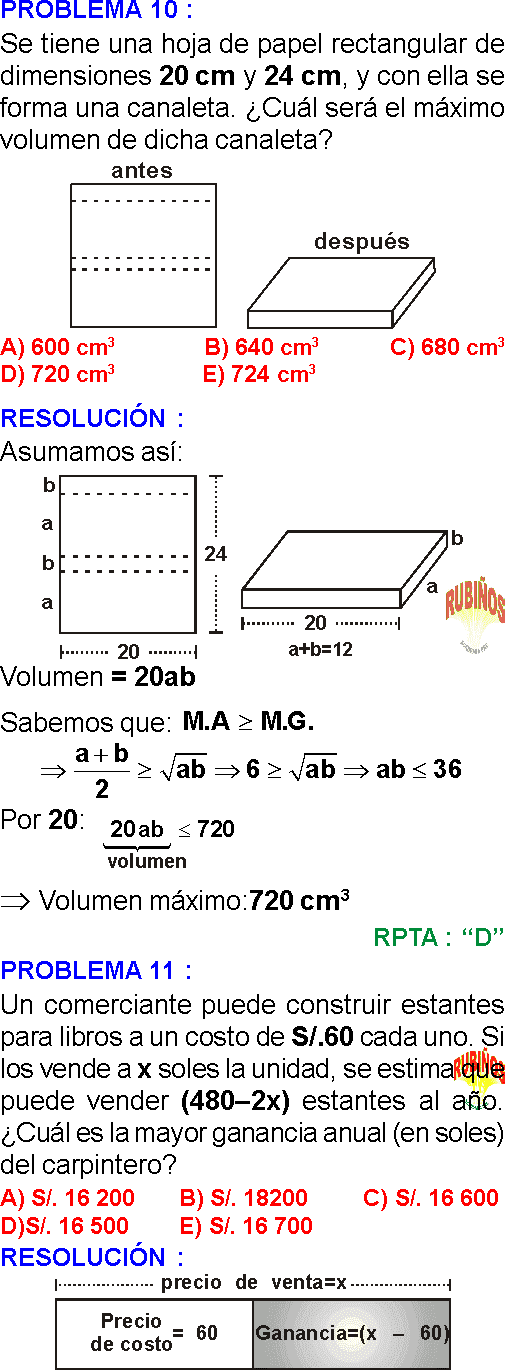
Se tiene un trozo de hojalata (de espesor despreciable) de forma rectangular de dimensiones 24 cm y 28 cm y con ella se forma una canaleta (ver figura). ¿Cuál será el máximo volumen que puede alcanzar en la canaleta?
A) 1200 cm³
B) 1076 cm³
C) 1286 cm³
D) 1176 cm³
RESOLUCIÓN :
PREGUNTA 6 :
La altura que alcanza un aeroplano de juguete depende del peso que este lleva. Si x representa el peso en kilogramos que se coloca en el aéreo plano y su altura en metros está dada por:
H = 40x – x² – 300
¿Cuál es la máxima altura en metros que alcanzará ese juguete y el peso en kilos que llevará para lograr tal altura? De como respuesta la suma de estos resultados.
A) 120
B) 140
C) 100
D) 150
RESOLUCIÓN :
PREGUNTA 7 :
El gasto en miles de soles de una determinada empresa está dado por:
Donde x representa el número de cientos de unidades vendidas, ¿cuántas unidades deben venderse para que el gasto sea mínimo?
A) 12
B) 500
C) 1400
D) 1200
RESOLUCIÓN :
PREGUNTA 8 :
En la figura, se representada una cancha de fulbito. Krily parte del punto A, y debe hacer el recorrido mostrado. ¿Cuál es la longitud del recorrido mínimo qué Krily puede hacer?
A) 4√61 m
B) 32 m
C) 28 m
D) 30 m
RESOLUCIÓN :
Aplicando simetría, hallaremos el recorrido mínimo:
PREGUNTA 9 :
Mile realiza el recorrido mostrado, desde el punto A y termina en el punto B, en un cuarto cuyas paredes son perpendiculares y cuyo plano se muestra en la figura. ¿Cuál es la longitud del recorrido mínimo de Mile?
A) 6,5 m
B) 6 m
C) 5,5 m
D) 5,8 m
RESOLUCIÓN :
PREGUNTA 10 :
En una plantación, la producción mensual de arroz está dada en kilogramos y depende de la cantidad de litros de agua por metro cuadrado utilizada en el riego, la cual está representada por x. Si la producción está dada por la función
P(x)= 1000x – x² – 200 000
¿Cuál es la producción máxima de arroz en kilogramos que puede haber en un mes?
A) 50 000
B) 20 000
C) 40 000
D) 500 000
E) 25 000
RESOLUCIÓN :
La producción de arroz está dada por la ecuación:
P(x)= – (x² – 2×500x + 250 000 ) – 200 000 + 250 000
P(x)= 50 000 – ( x – 500)²
Cuando la cantidad de agua por metro cuadrado al regar sea de 500 litros la producción mensual de arroz máxima puede ser 50 000 Kg.
Rpta. : "A"
PREGUNTA 11 :
Raúl es un negociante que vende azúcar al por menor. Si él, solo dispone de una gran cantidad de bolsas de plástico, con capacidades de 1 Kg, 3 Kg y 9 Kg; ¿cuántas bolsas como mínimo empleara para almacenar 376 kg de azúcar?
A) 44
B) 46
C) 48
D) 38
E) 42
RESOLUCIÓN :
Para almacenar 376 kg de azúcar empleara:
X bolsas de 1 kg
Y bolsas de 3kg
Z bolsas de 9 kg, luego: x + 3y + 9z = 376
Para emplear la mínima cantidad de bolsas, debe emplear la mayor cantidad de bolsas de 9 kg.
Luego 376 = 9 (41) + 7
Luego 1 + 3(2) + 9(41) = 376
1 bolsa de 1 kg
2 bolsas de 3kg
41 bolsas de 9kg, total empleara: 41 + 1 + 2 = 44
Rpta. : "A"
PREGUNTA 12 :
En la figura, se muestra dos bloques de cemento cada uno en forma de paralelepípedo. Si una araña ha muerto y está ubicada en el punto medio de la cara frontal del bloque más alto y una hormiga está ubicada en el punto medio de la cara lateral derecha del bloque más pequeño, ¿cuál es la mínima longitud que debe recorrer la hormiga para llegar hasta donde está la araña?
A) 10√10 cm
B) 8√10 cm
C) 9√11 cm
D) 8√13 cm
E) 40 cm
RESOLUCIÓN :
Desarrollando el sólido se tiene la siguiente figura:
Rpta. : "A"
PREGUNTA 13 :
Eloy se propone dibujar una línea, de longitud mínima, que inicie en A, pase por un punto P de la recta L, y finalice en el punto B. Indique la suma de las coordenadas del punto P.
A) 8
B) 9
C) 5
D) 6
E) 7
RESOLUCIÓN :
Para ubicar el punto P sobre la recta, se ubica el Punto A1, simétrico de A respecto de la recta. Entonces el punto P se ubica en la intersección de la recta y el segmento A1B.
Con la ayuda de la cuadrícula se obtiene las Coordenadas de P, que son (4,1) Por lo tanto, la suma de coordenadas de P es 5.
Rpta. : "C"
PREGUNTA 14 :
La figura muestra cinco fichas cuadradas, cada una con un número. Si solo estas fichas pueden cambiar de lugar, ¿cuál es el mínimo valor entero que puede tomar S?
A) 0
B) 4
C) 3
D) 1
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 15 :
¿Cuál es el área máxima de la región que se muestra en la figura si se sabe que su perímetro es 60 cm?
A) 196 cm²
B) 175 cm²
C) 225 cm²
D) 216 cm²
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 17 :
Se corta un alambre de dos metros de longitud en dos partes para formar, con una de ellas, un triángulo equilátero y, con otra, un cuadrado. Si se quiere que la suma de las áreas de ambas figuras sea mínima, ¿a qué distancia de uno de los extremos del alambre se debe hacer el corte?
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 18:
La figura 1 representa un vaso que tiene la forma de un cilindro circular recto cuyo radio de la base mide 4 cm y la figura 2 representa una bandeja rectangular. ¿Cuántos vasos idénticos como los de la figura 1 se pueden colocar, como máximo, sobre la bandeja representada por la figura 2, sin que estos se desborden ni se apilen uno sobre otro?
A) 10
B) 12
C) 14
D) 11
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 19 :
En un baúl hay 5 cofres, en cada cofre hay 3 cajas, y en cada caja hay 10 monedas de oro. El baúl, los cofres y las cajas están cerrados con llave. ¿Cuál es la menor cantidad de cerraduras hay que abrir para obtener 50 monedas?
A) 10
B) 8
C) 6
D) 5
E) 3
RESOLUCIÓN :
• Hay que abrir 5 cajas, que están contenidas en al menos 2 cofres, que están dentro del baúl.
• Número de cerraduras = 5+2+1=8
Rpta. : "B"
PREGUNTA 20 :
Diego trabaja 4 días de la semana y descansa el quinto. En una ocasión empezó a trabajar un lunes y descansó un día domingo. ¿Cuál es la menor cantidad de días que tuvo que trabajar para que esto fuera posible?
A) 7
B) 12
C) 20
D) 28
E) 36
RESOLUCIÓN :
• Empieza Lunes y descansa Domingo, entonces el número de días es múltiplo de 7 .
• Como descansa cada quinto día, entonces el número de días debe ser múltiplo de 5 .
• El número de días es mínimo, luego es el mcm (7;5) =35.
• El número de días que trabaja= 4/5 × 35 = 28
Rpta. : "D"
PREGUNTA 21 :
En cada casilla de la cuadrícula debemos escribir números enteros positivos distintos de modo que en cada fila, de izquierda a derecha, cada uno de los números sea múltiplo del que le precede y lo mismo en cada columna, de arriba a abajo. ¿Cuál es el menor número que se debe escribir en la casilla sombreada?
A) 120
B) 72
C) 60
D) 32
E) 64
RESOLUCIÓN :
El menor valor para la casilla sombreada se obtiene si en la casilla superior izquierda se escribe el 1 luego multiplicar por 2 hacia la derecha y por 3 hacia abajo.
Por lo tanto, en la casilla sombreada se debe escribir el 72.
Rpta. : "B"
PREGUNTA 22 :
En un concurso de matemáticas hubo 100 competidores que tenían que resolver 4 problemas. Resultó que 90 concursantes resolvieron el primer problema, 85 resolvieron el segundo, 80 resolvieron el tercero y 70 resolvieron el cuarto.
¿Cuál es el mínimo número posible de concursantes que resolvieron los 4 problemas?
A) 12
B) 10
C) 15
D) 20
E) 25
RESOLUCIÓN :
• Se puede asegurar que al menos 85–(100–90)=75 resolvieron los dos primeros problemas.
• Que 80–(100–75) = 55 resolvieron los tres primeros problemas.
• Por lo tanto, al menos 70–(100–55) = 25 resolvieron los cuatro problemas.
Rpta. : "E"
PREGUNTA 23 :
En el país FFF el pie izquierdo de cada hombre es dos números más grande que su pie derecho, y el pie izquierdo de cada mujer es un número más grande que el derecho. Sin embargo, los zapatos se venden por pares del mismo número. Para ahorrar, un grupo de amigos compró una colección de zapatos. Al final sobraron sólo dos zapatos: uno de talla 21 y otro de talla 30. ¿Cuál es el mínimo número posible de personas en ese grupo?
A) 5
B) 6
C) 7
D) 8
E) 9
RESOLUCIÓN :
• Como 21 es impar y 30 es par, por lo menos hay una mujer.
• 30=21+1+2++2+2+2, que son 5 personas.
• Los zapatos pudieron agruparse como sigue:
• (21,22), (22,24), (24,26), (26,28) y (28,30)
Rpta. : "A"
PREGUNTA 24 :
Edu dispone de siete piezas de alambre, cuyas longitudes son: 1, 2, 3, 4, 5, 6 y 7 cm, con dichas piezas se propone construir un cubo como el que se representa en la figura. Si las piezas no deben ser cortadas ni superpuestas, ¿cuántas piezas, como mínimo, empleará para construir dicho cubo?
A) 3
B) 5
C) 2
D) 4
E) 1
RESOLUCIÓN :
Como mínimo se usan 4 piezas, las de 6, 2, 3 y 1 cm
Rpta. : "D"
PREGUNTA 25 :
Anita dispone de fichas de madera como la que se indica en la figura. Cada ficha está formada por 3 cuadrados congruentes de 1 cm de lado. ¿Cuántas fichas, como mínimo, empleará para construir una figura de forma cuadrada?
A) 9
B) 15
C) 12
D) 24
E) 18
RESOLUCIÓN :
• Si el cuadrado que se construye tiene k piezas, entonces 3k debe ser un cuadrado perfecto.
• 3k =m² → k =3n² ;m y n∈ℤ
• Si n=1, entonces k=3. Es fácil observar que con 3 piezas no se puede formar un cuadrado.
• Si n=2, entonces k=12.
Y con 12 piezas si es posible construir un cuadrado.
Rpta. : "C"
PREGUNTA 26 :
Cianina ha apilado 14 cajas que contienen canicas, tal como se muestra en la figura. Se sabe que en las cajas de la base hay en total 50 canicas, y que cada una de las cajas de los otros niveles contiene tantas canicas como las cuatro cajas juntas en las que se apoya. ¿Cuántas canicas como máximo contiene la caja del nivel superior?
A) 216
B) 198
C) 180
D) 155
E) 170
RESOLUCIÓN :
Para calcular la cantidad de canicas que contiene la caja superior, los contenidos de las cajas de las esquinas de la base se suman una vez, el del centro de la base se suma 4 veces y los 4 restantes de la base 2 veces. Claramente, conviene colocar en todas las cajas de la base (menos en el del centro) una canica, y en la caja del centro 42 canicas. Así, el número de canicas que contiene la caja superior sería máxima e igual a 45×4 = 180
Rpta. : "C"
PREGUNTA 27 :
Luis cambia 2 billetes de 200 soles por monedas de S/ 5; S/ 2; S/ 1; S/ 0,5; S/ 0,2 y S/ 0,1. Si le dan todos los tipos de monedas y la cantidad de monedas de S/ 2 que le dan es la máxima posible, determine la menor cantidad de monedas recibidas por Luis.
A) 203
B) 86
C) 114
D) 170
E) 87
RESOLUCIÓN :
400=1(5)+196(2)+2(1)+1(0,5)+2(0,2)+1(0,1)
Total de monedas :1+196+2+1+2+1=203
Rpta. : "A"
PREGUNTA 28 :
Para participar de un juego, se debe pagar S/ 4,00. Para este juego, se dispone de varias bolsitas que contienen cada una, 4 monedas o 7 monedas de S/ 1,00. Sin abrir las bolsitas, se denota con P, al conjunto que contiene a todas las posibles cantidades, que se puede formar reuniendo las bolsitas. Un participante se llevará la cantidad en soles que pertenece a P, si elige un número que está en P pero cuya ganancia que tendría el jugador no pertenece a P. ¿Cuál es la máxima ganancia en soles, que un participante puede obtener en este juego?
A) 25
B) 23
C) 17
D) 10
E) 21
RESOLUCIÓN :
Con bolsitas de S/ 4.00 y de S/ 7.00, se puede formar el siguiente conjunto:
P={ 4, 7, 8, 11, 12, 14, 15, 16, 18, 19, 20, 21, 22, 23, 24, ….}
(conjunto de premios)
Pero como paga S/ 4.00 sus posibles ganancias serían:
G= { 0, 3, 4, 7, 8, 10, 11, 12, 14, 15, 16, 17, 18, 19. 20, …}
Pero en realidad los premios se reciben solo si, las respectivas ganancias no pertenecen a p:
G – P = { 0, 3, 10, 17}
Máxima ganancia de un participante: S/ 17.00
Rpta. : "C"
PREGUNTA 29 :
En una chocolatería se encuentran 28 personas, las cuales han comprado por lo menos una caja de chocolates. De estas personas se sabe que: 23 compraron dos o más cajas de chocolates, 16 compraron tres o más cajas de chocolates, 14 compraron cuatro o más cajas de chocolates, 7 compraron cinco o más cajas de chocolates y 4 compraron exactamente 6 cajas de chocolates. Si ninguna persona compró más de 6 cajas de chocolate, ¿cuántas cajas de chocolates como mínimo se compraron en total?
A) 94
B) 96
C) 95
D) 91
E) 92
RESOLUCIÓN :
Del problema tenemos:
23 compraron 2 o más cajas
16 compraron 3 o más cajas
14 compraron 4 o más cajas
7 compraron 5 o más cajas
4 compraron exactamente 6 cajas
Como se quiere el mínimo número de cajas hacemos el siguiente análisis:
Si 23 compraron 2 o más cajas y 16 compraron 3 o más cajas entonces 7 compraron 2 cajas y 16 compraron 3 o más cajas
Si 16 compraron 3 o más cajas y 14 compraron 4 o más cajas entonces 2 compraron 3 cajas y 14 compraron 4 o más cajas
Si 14 compraron 4 o más cajas y 7 compraron 5 o más entonces 7 compraron 4 cajas y 7 compraron 5 o más.
Si 7 compraron 5 o más cajas y 4 compraron 6 cajas entonces 3 compraron 5 cajas.
Como ninguna persona compró más de 6 cajas de chocolate y el total de personas en la tienda son 28 entonces quiere decir que 5 personas compraron una caja de chocolate.
Luego el total mínimo de cajas compradas fue: 7×2+2×3+7×4+3×5+4×6+5×1=92
Rpta. : "E"
PREGUNTA 30 :
¿Cuántas cifras, como máximo, pueden ser borradas del numeral de 1000 cifras: 201920192019…2019, de tal manera que la suma de las cifras restantes sea 2019?
A) 772
B) 776
C) 780
D) 774
E) 778
RESOLUCIÓN :
Hay en el numeral de 1000 cifras:
cifras 2: 250
cifras 0: 250
cifras 1: 250
cifras 9: 250
Para que puedan ser borrados el máximo número de cifras, deben quedar las cifras de mayor valor tal que sumen 2019.
Suma de las cifras restantes: 9(224)+2(1)+1(1)=2019
Por tanto, como máximo de cifras, se pueden borrar: 1000 – (224+1+1)=774
Rpta. : "D"
PREGUNTA 31 :
En un país, solo admiten dos tipos de monedas, una que equivale a 4 soles y otra equivalente a 9 soles y con ellas hacen sus transacciones monetarias. ¿Cuál es la mayor cantidad, en soles, que no pueden obtener con sus monedas?
A) 23
B) 29
C) 15
D) 17
E) 19
RESOLUCIÓN :
Cantidades que pueden obtener con sus monedas:
0, 4, 8, 9, 12, 13, 16, 17, 18, 20, 21, 22, 24, 25, 26, 27, 28, 29, …
Por tanto, la máxima cantidad, que no pueden obtener es 23 soles.
Rpta. : "A"
PREGUNTA 32 :
Fernando un hábil estudiante de la U , al conversar con un electricista este le comenta que el día de ayer tuvo que subir 9 veces por el ascensor del edificio hasta el piso 8, ya que en dicho piso hay 9 cuartos completamente cerrados cada uno con solo una puerta de acceso y dentro de cada cuarto un foco. Pero los 9 interruptores que los prenden se encontraban en el primer piso, pero no se sabía que interruptor correspondía a cada foco. Si Fernando, luego de pensar un momento le dice que solo era necesario subir “x” veces como mínimo. ¿Cuántas veces como mínimo se tendría que subir por el ascensor hasta el piso 8, para saber con seguridad que interruptor corresponde a cada foco? (Solo se puede subir por el ascensor y si un foco se enciende éste se calienta)
A) 5
B) 2
C) 3
D) 4
E) 9
RESOLUCIÓN :
• Se prenden tres focos por 10 minutos, luego se los apaga y se prenden otros tres focos, se sube por primera vez por el ascensor y se averigua cuáles son esos tres focos prendidos.
• De los cuartos que tienen los focos apagados se toca cada uno de ellos para averiguar si están calientes o fríos, de esa forma se sabrá que los tres focos calientes corresponden a los tres primeros interruptores que se prendió, y los tres interruptores que no se prendió corresponden a los tres focos fríos.
• Separamos los grupos de: tres interruptores de focos fríos, tres interruptores de focos calientes y tres interruptores de focos prendidos.
• De los tres interruptores de focos fríos, se prende uno por 10 min se apaga y se prende otro; se prende uno de los interruptores de focos apagados; se apaga uno de los tres interruptores de focos pendidos. Se sube por segunda vez por el ascensor.
• De esa forma se podrá saber que interruptor corresponde a cada uno de los tres focos que estaban fríos inicialmente. También se podrá identificar un interruptor de los focos tibios y un interruptor de los focos prendidos. Solo faltaría identificar dos focos prendidos y dos focos apagados tibios.
• Del grupo de los focos prendidos se apaga uno; del grupo de los focos apagados y tibios se prende uno y se sube por tercera vez. De esa forma ya se podría identificar los 9 interruptores que corresponden a los 9 focos.
Rpta. : "C"
PROBLEMAS PROPUESTOS
PREGUNTA 1 :
Hallar el máximo valor de M:
M = 200 – (x – 3)²
A) 200
B) 100
C) 0
D) 300
E) 400
PREGUNTA 2 :
Hallar el máximo valor de M:
M = –x² – 20x – 100
A) 0
B) 1
C) 100
D) 20
E) 4
PREGUNTA 3 :
Si: a + b = 12
hallar al máximo valor de: a × b
A) 36
B) 49
C) 50
D) 90
E) 100
PREGUNTA 4 :
Si: a + b + c + d = 6, hallar el máximo valor de M.
M = (ac + ad + bc + bd)²
A) 81
B) 36
C) 49
D) 20
E) 10
PREGUNTA 5 :
Un carpintero puede construir estantes para libros a un costo de 60 soles cada uno. Si los vende a “x” soles la unidad, se estima que puede vender “480 – 2x” estantes al año, ¿cuál sería la mayor ganancia anual (en soles) del carpintero?
A) 16200
B) 28800
C) 14400
D) 20000
E) 24300
Rpta. : "A"
PREGUNTA 6 :
Lenin desea comprar un terreno de forma rectangular con la condición de que el doble del perímetro del terreno exceda en 168 m al ancho del terreno. Halle el área máxima del terreno que puede comprar Lenin.
A) 588m²
B) 630 m²
C) 300m²
D) 672m²
E) 540 m²
Rpta. : "A"
PREGUNTA 7 :
Elvis lanza tres dados convencionales: un blanco, un negro y un azul. Recibirá en soles, la siguiente cantidad: 4 veces el puntaje del blanco, más 3 veces el del azul, más dos veces el del dado negro, menos el producto de los puntajes obtenidos con el blanco y el negro. Si Ulises obtuvo la máxima cantidad de dinero posible, ¿cuál es el puntaje total que obtuvo con los tres dados?
A) 11
B) 14
C) 10
D) 13
E) 18
Rpta. : "D"
PREGUNTA 8 :
El matrimonio Merino , decide repartir a sus hijos en calidad de herencia, parcelas de terreno de forma rectangular. A Lewis el hijo mayor le corresponde una parcela en la cual se cumple que el doble del perímetro excede en 168 m al ancho de la misma. Halle el área máxima de la parcela de terreno que le corresponde a Lewis.
A) 576 m²
B) 586 m²
C) 546 m²
D) 588 m²
E) 648 m²
Rpta. : "D"
PREGUNTA 9 :
Un fabricante de alfombras observa que las ventas mensuales de x unidades del mencionado artículo cuando su precio unitario es P soles están dadas por P=205 – 3x . Si el costo de producir unidades del mismo artículo es C=970 + 4x soles. ¿Cuántas unidades como mínimo de este artículo deberán producirse y venderse de modo que la utilidad mensual sea por lo menos de 2000 soles?
A) 22
B) 25
C) 23
D) 45
E) 24
Rpta. : "A"
PREGUNTA 10 :
Los dieciséis dígitos del número de una tarjeta de crédito, tienen la condición de que la suma de tres dígitos cualesquiera, ubicados consecutivamente, siempre da 20. Si lo contamos de derecha a izquierda, el tercer dígito es 5, ¿cuál es el mínimo valor del último dígito?
A) 4
B) 5
C) 6
D) 7
E) 8
Rpta. : "C"
PREGUNTA 11 :
Como parte de la programación del aniversario de una Institución Educativa, 50 alumnos participaron en una maratón de 1Km de distancia, donde todos llegaron a la meta en instantes diferentes. Cuando se les preguntó, ¿en qué lugar llegaron?, cada uno de ellos contestó con un número entero del 1 al 50. Si la suma de las respuestas fue de 1000, ¿cuántas respuestas, como mínimo, fueron falsas?
A) 8
B) 4
C) 7
D) 6
E) 5
Rpta. : "D"
PREGUNTA 12 :
Cierta Universidad ofrece un taller de capacitación. La inscripción por persona es de S/ 80 y asisten al taller 600 personas, pero por cada disminución de S/ 2 en la inscripción asisten 10 personas más, y por cada aumento de S/ 2 en la inscripción asisten 10 personas menos. Para obtener la máxima recaudación posible, ¿cuánto debe ser el costo de la inscripción a cobrar?
A) S/ 80
B) S/ 60
C) S/ 40
D) S/ 100
E) S/ 120
Rpta. : "D"
PREGUNTA 13 :
En una panadería, los sándwiches cuestan 54 soles el ciento. Un kilo de bombones más un kilo de orejitas cuesta tanto como 50 sándwiches. Un kilo de bombones cuesta tanto como un kilo y cuarto de orejitas. María fue a la panadería con un número entero de soles. Después de comprar 75 sándwiches, lo que le quedó le alcanzaba para comprar 1 kilo de bombones pero no le alcanzaba para comprar 1 kilo y medio de orejitas. ¿Cuánto dinero como máximo llevó María ?
A) S/ 55
B) S/ 56
C) S/ 57
D) S/ 58
E) S/ 59
Rpta. : "D"
PREGUNTA 14 :
Una empresa embotelladora de limonada desea obtener la mayor ganancia por la venta de sus refrescos. Su producción máxima de limonada es de 1000 botellas de un litro por día, vendiendo cada una de ellas a S/ 2. El agua para preparar la limonada lo compra solo por paquetes de 15 unidades cada uno y de las siguientes marcas: La marca “A” a S/ 18 el paquete y cada envase de 650 ml; la marca “B” a S/ 22,5 el paquete y cada envase de 600 ml; la marca “C” a S/ 15 el paquete y cada envase de 625 ml. Si de cada marca de agua se debe llenar una cantidad exacta de botellas y utiliza agua de las tres marcas, ¿cuál sería la mayor ganancia obtenida en un día al vender la máxima cantidad de botellas de limonada?
A) S/ 393
B) S/ 400
C) S/ 410
D) S/ 354
E) S/ 363
Rpta. : "E"
PRACTICA DE CLASE CON RESPUESTAS AL FINAL
PREGUNTA 1 :
Sean los números
a=24 – 2x
b=3x – 30
c =x+18
Si x ∈ ℜ , determine el valor de c cuando a×b toma su máximo valor.
A) 20
B) 18
C) 31
D) 29
PREGUNTA 2 :
Se desea cercar el jardín mostrado en el gráfico utilizando para ello 32 m de cerca. ¿Cuál es el área máxima que puede tener dicho jardín?
A) 120 m²
B) 64 m²
C) 96 m²
D) 32 m²
PREGUNTA 3 :
Estela se dedica a la compra y venta de celulares. Cada mes compra x celulares por un valor de S/6x cada uno y los vende por internet a S/420 cada uno. ¿Cuál es la máxima ganancia que Estela puede conseguir en un mes?
A) S/2450
B) S/7350
C) S/8250
D) S/7680
PREGUNTA 4 :
El área de la región circular es 16𝛑 u². Calcule el área máxima del rectángulo ABCD.
A) 32 u²
B) 28 u²
C) 17 u²
D) 32𝛑−¹ u²
PREGUNTA 5 :
Edu y Bruno tienen cada uno una cierta cantidad de canicas. Edu indica que el doble de canicas que él tiene y el triple de canicas de Bruno suman 45. Bruno dice que si Edu le diera 5 canicas el producto del número que canicas que tendríamos sería máximo. Halle la cantidad de canicas que tiene Bruno.
A) 12
B) 15
C) 16
D) 18
PREGUNTA 6 :
La cantidad de autos vendidos en el último mes del año está dada por la expresión
V(x) =x² – 60x+1150
Donde x representa el ahorro en miles de soles que todos los clientes han alcanzado en el mes de julio. ¿Cuál es el mínimo número de autos que se venderá en este mes?
A) 330
B) 180
C) 280
D) 250
PREGUNTA 7 :
Una hormiga, ubicada en el punto A, desea desplazarse por la superficie del ladrillo mostrado hasta el punto B. ¿Cuál será la mínima longitud de su recorrido?
A) 7√5 cm
B) 14 cm
C) 15 cm
D) 16 cm
PREGUNTA 8 :
Una empresa ha notado que si vende cada uno de sus artículos a S/12 habría 600 personas que podrían comprar, cada uno de ellos, un artículo. Además, que cada vez que aumentan en S/1 el costo de cada artículo la cantidad de personas que podría adquirir un artículo disminuye en 25. ¿A qué precio debe fijar cada artículo si se desea obtener la máxima recaudación?
A) S/15
B) S/12
C) S/18
D) S/21
PREGUNTA 9 :
Halle el máximo valor del área de la región sombreada si AC=12 cm².
A) 36 cm²
B) 9 cm²
C) 6√2 cm²
D) 16 cm²
PREGUNTA 10 :
Una huerta tiene actualmente 26 árboles que producen 600 frutos cada uno. Se conoce que por cada árbol adicional plantado la producción de cada árbol, disminuye en 15 frutos. ¿Cuál debe ser el número total de árboles que debe tener la huerta, para que la producción sea máxima?
A) 33
B) 25
C) 37
D) 28
PREGUNTA 11 :
Un juego consiste en lanzar una pelota desde el lugar indicado y hacer que esta golpee la pared A y luego la pared B hasta llegar a tumbar la lata. ¿Qué tiempo empleará, como mínimo, para lograrlo si la pelota debe salir con rapidez constante de 3 m/s?
A) 20 s
B) 10 s
C) 15 s
D) 25 s
PREGUNTA 12 :
En la figura se muestran las dimensiones, en metros, de una piscina que tiene forma rectangular. Si x es un número real positivo, ¿cuál es el área máxima, en metros cuadrados, que podría tener dicha piscina?
A) 42 m²
B) 48 m²
C) 50 m²
D) 52 m²
PREGUNTA 13 :
En el cilindro recto mostrado, una arañita ubicada en el punto A desea realizar el recorrido mostrado (rodeando el cilindro) hasta llegar al punto B donde está su comida. ¿Cuál es la longitud mínima de dicho recorrido?
A) 25π cm
B) √61 cm
C) 11π cm
D) 13π cm
PREGUNTA 14 :
El gráfico muestra una mesa de billar y una bola de billar que debe realizar el recorrido mostrado hasta llegar al agujero. ¿Cuál es la menor longitud recorrida por dicha bola?
A) 6√5 cm
B) 9√2 cm
C) 13 cm
D) 11 cm
CLAVES – RESPUESTAS : 1)D 2)B 3)B 4)A 5)B 6)D 7)C 8)C 9)B 10)A 11)A 12)C 13)D 14)C






















.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)









.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)

.png)
.png)
.png)

