ÁNGULO TRIPLE EJERCICIOS RESUELTOS DE IDENTIDADES TRIGONOMÉTRICAS DE UN ARCO TRIPLE PDF
RAZONES TRIGONOMÉTRICAS DE UN ARCO TRIPLE
APRENDIZAJES ESPERADOS
• Conocer y utilizar las identidades trigonométricas de un ángulo triple.
• Realizar operaciones de simplificación utilizando las identidades del triple
• Entender la relación entre las razones trigonométricas de un arco triple ; así como expresiones simplificadas para hacer un análisis más preciso.
• Aplicar las identidades trigonométricas en la simplificación de expresiones trigonométricas
• Contextualizar en lo cotidiano las identidades trigonométricas de arcos múltiples.
SENO DEL ARCO TRIPLE
Sen3x = 3Senx – 4Sen³x
DEMOSTRACIÓN :
Notamos que: Sen3x = Sen(2x + x)
= Sen2x.Cosx + Cos2x.Senx
= (2Senx.Cosx)Cosx + Senx.Cos2x
= 2Senx.Cos²x + Senx(1 – 2Sen²x)
= 2Senx(1 – Sen²x) + Senx – 2Sen³x
= 2Senx – 2Sen³x + Senx – 2Sen³x
∴ Sen3x = 3Senx – 4Sen³x
EJEMPLOS :
• Sen12θ = Sen3(4θ) = 3Sen4θ – 4Sen³4θ
• Sen21º = Sen3(7º) = 3Sen7º – 4Sen³7º
• 3Sen10º – 4Sen³10º = Sen3(10º) = Sen30º =1/2
COSENO DEL ARCO TRIPLE
Cos3x = 4Cos³x – 3Cosx
DEMOSTRACIÓN :
Notamos que: Cos3x = Cos(2x + x)
= Cos2x.Cosx – Sen2x.Senx
= Cosx.Cos2x – (2Senx.Cosx)Senx
= Cosx(2Cos²x – 1) – 2 Cosx.Sen²x
= 2Cos³x – Cosx – 2Cosx(1 – Cos²x)
= 2Cos³x – Cosx – 2Cosx + 2Cos3x
∴ Cos3x = 4Cos³x – 3Cosx
EJEMPLOS :
• Cos24º = Cos3(8º) = 4Cos³8º – 3Cos8º
• Cos9β = Cos3(3β) = 4Cos³3β – 3Cos3β
• 4Cos³(60º+θ)–3Cos(60º+θ) = Cos3(60º+θ) = Cos(180º+3θ) = – Cos3θ
• 4Cos³8º20’ – 3Cos8º20’ = Cos3(8º20’) = Cos24º60’ = Cos25º
PRACTICA
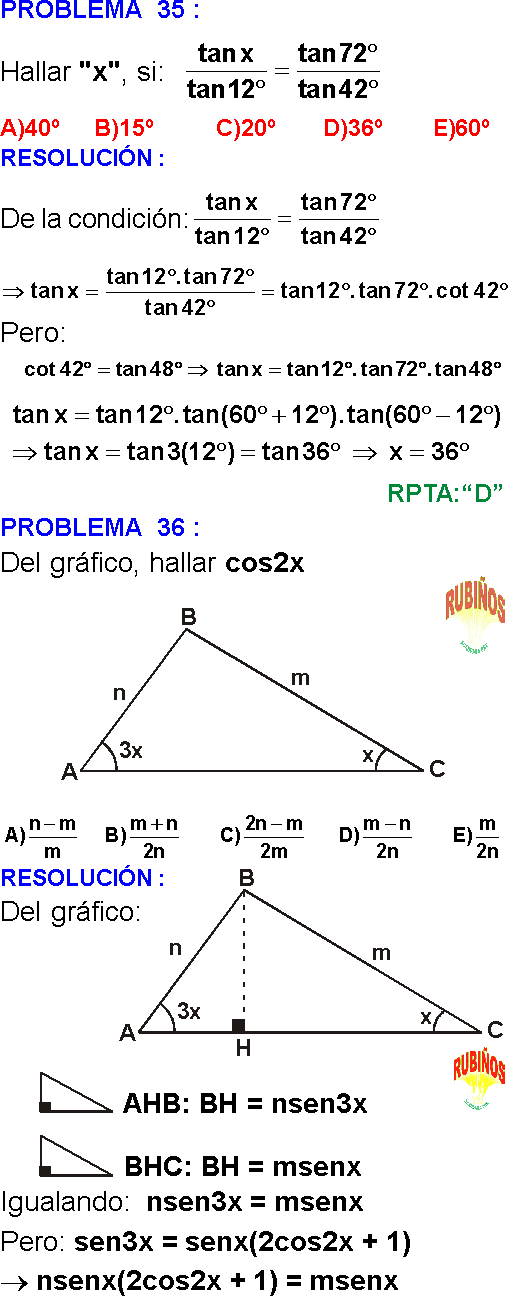
PROBLEMA 1 :
Calcule el valor de: Sen159°
a) 117/225
b) 107/225
c) 44/225
d) 44/125
e) 22/225
Rpta. : "D"
PROBLEMA 2 :
Calcule:
3sen50º – 4sen³50º
A) 1/4
B) 0,45
C) 4
D) 6
E) 0,5
Rpta. : "E"
PROBLEMA 3 :
Si cosω= 1/3
Calcule cosω
A) –1/47
B) –23/27
C) 4/9
D) 6/7
E) 5/8
Rpta. : "B"
PROBLEMA 4 :
Si tgθ= 0,25
Calcule 52tg3θ
A) 34
B) 47
C) 49
D) 67
E) 51
Rpta. : "B"
PROBLEMA 5 :
Si tg(δ + 15º) = 1/2
Calcule tg3δ
A) 9/13
B) 7/9
C) 4/7
D) 6/7
E) 5/9
Rpta. : "A"
PROBLEMA 6 :
Reduzca:
9sen²σ + 16sen⁶σ – 24sen⁴σ
A) sen²2σ
B) 0
C) sen²3σ
D) 1
E) sen²σ
Rpta. : "C"
PROBLEMA 7 :
Calcule: sec40º + 8cos240º
A) –6
B) –5
C) 4
D) 6
E) 5
Rpta. : "D"
PROBLEMA 8 :
Si tg³φ – 3√2 tg²φ – 3tgφ + √2 = 0
Calcule tg6φ
A) –6√2
B) –5√2
C) –2√2
D) 6
E) 5
Rpta. : "C"
PROBLEMA 9 :
Calcular: Sec20°.Sec40°.Sec80°
a) 8
b) 6
c) 16
d) 4
e) 32
Rpta. : "A"
PROBLEMA 10 :
Reduzca: 16Cos⁶x – 24Cos⁴x + 9Cos²x
a) 3Senx
b) 3Cosx
c) Cos²3x
d) Cos³3x
e) Cos⁴3x
Rpta. : "C"
PROBLEMA 11 :
Reduzca: 3Tan²ψ ·Tan3ψ + 3Tanψ – Tan3ψ
a) Tanψ
b) Tan3ψ
c) Tan6ψ
d) Cotψ
e) Cot3ψ
Rpta. : "B"
PROBLEMA 12 :
Indique el equivalente de: Tan²20°.Tan²40° + Cot²80°
a) 2Tan10°
b) 4Tan10°
c) 2Tan²10°
d) 4Tan²10°
e) 2Tan 20°
Rpta. : "D"
PROBLEMA 13 :
¿A qué es equivalente: √3 +6Cos10°?
a) Sen10°
b) Sen³10°
c) 8Sen²10°
d) 8Cos³10°
e) 8Sen³10°
Rpta. : "D"
PROBLEMA 14 :
Calcular: Sen10°.Sen50°.Sen70°
a) 1/2
b) 1/4
c) 1/8
d) 1/16
e) 1/32
Rpta. : "C"
PROBLEMA 15 :
Simplifique: H = (4sen³x + sen3x)cscx
A) 1
B) 2
C) 3
D) 4
E) 5
Rpta. : "C"
PROBLEMA 16 :
Calcule el valor de:
cos20º(2cos40º – 1) + sen10º(2cos20º + 1)
A) 3
B) –2
C) –1
D) 2
E) 1
PROBLEMA 17 :
Calcule:
csc70º− 8sen²70º
A) –6
B) –5
C) 4
D) 6
E) 5
PROBLEMA 18 :
Si senφ + cosφ = 0,8
Calcule: cos3φ – sen3φ
A) 1,376
B) 0,225
C) 0,169
D) 0,144
E) 0,121
DEGRADACIÓN DEL EXPONENTE “3” Ó “CUBO”
Las fórmulas expuestas a continuación son empleadas en las expresiones trigonométricas, donde se presenten “senos” o “cosenos” de un cierto arco elevado al exponente “3”.
Degradación del “Cubo” del seno de un arco simple “x”