CUADRILÁTEROS EJERCICIOS RESUELTOS PDF

OBJETIVOS DEL APRENDIZAJE

• Diferenciar a los cuadriláteros según el paralelismo de sus lados opuestos.

• Identificar las diferentes propiedades según la clasificación de los cuadriláteros.

• Determinar el teorema a utilizar en los ejercicios, a partir de los datos y la disposición gráfica de los mismos.

• Analizar al paralelogramo a partir del paralelismo de sus lados.

• Reconocer las diferentes propiedades según la clasificación del paralelogramo.

• Relacionar correctamente el teorema con el ejercicio a partir del tipo de cuadrilátero.

CUADRILÁTERO

Es la figura formada por cuatro segmentos de recta no colineales donde los únicos puntos en común son sus extremos.

CLASIFICACIÓN DE LOS CUADRILÁTEROS

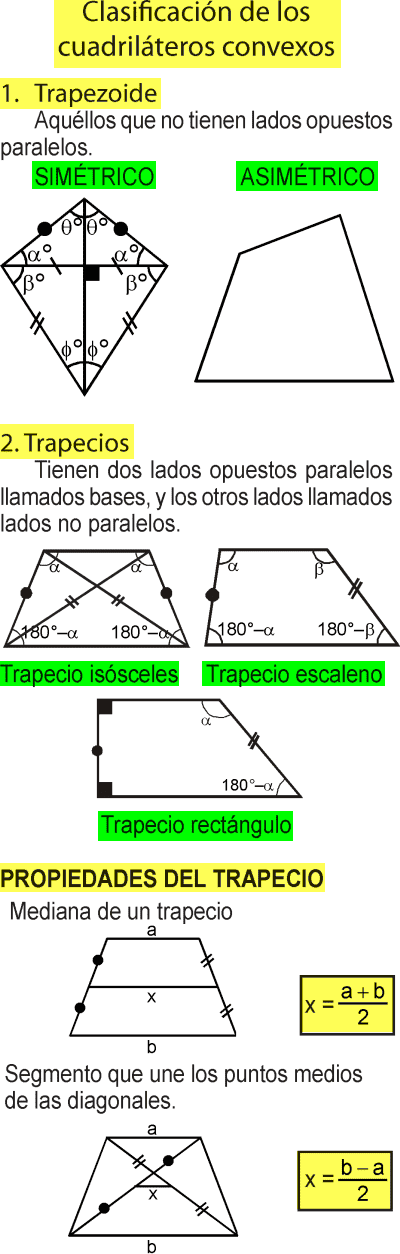
TRAPEZOIDE

Es el cuadrilátero cuyos lados opuestos no son paralelos

TRAPECIO

Es aquel cuadrilátero que presenta solo dos lados

PARALELOGRAMO

Es aquel cuadrilátero cuyos lados opuestos son paralelos.

Se cumple

• Los lados opuestos son de igual longitud.

• Los ángulos opuestos son de igual medida.

• Los ángulos adyacentes son suplementarios (suman 180°).

En todo paralelogramo las diagonales se intersecan en su punto medio.

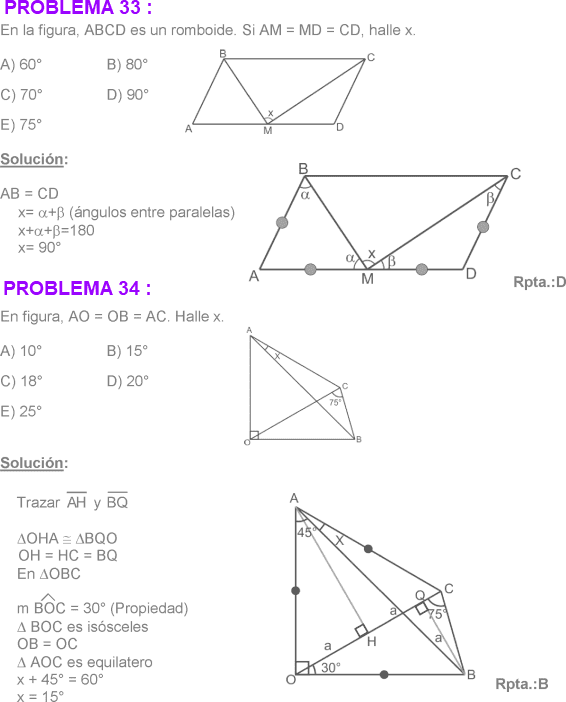
ROMBOIDE

Paralelogramo que tiene sus lados consecutivos de diferentes longitudes y sus ángulos internos no miden 90°.

RECTÁNGULO

Paralelogramo que tiene sus lados consecutivos de diferentes

CUADRADO

Paralelogramo cuyos ángulos internos miden 90° y sus lados son de igual longitud.

ROMBO

Paralelogramo cuyos ángulos internos no miden 90° y sus lados son de igual longitud.

EJERCICIOS PROPUESTOS

PREGUNTA 1 :

La suma de las distancias desde los vértices de un romboide a una recta exterior es 24u. Calcular la distancia del punto de intersección de las diagonales a la misma recta exterior al romboide.

A) 6u

B) 8

C) 10

D) 5

E) 4

Rpta. : "A"

PREGUNTA 2 :

La mediana de un trapecio mide 10, las longitudes de los lados no paralelos suman 18. Encontrar el perímetro del trapecio.

A) 20

B) 28

C) 36

D) 38

E) 42

Rpta. : "D"

PREGUNTA 3 :

Uno de los lados de un rectángulo es el doble del otro lado, el perímetro del rectángulo es 90. Encontrar la longitud del mayor lado.

A) 20

B) 25

C) 30

D) 35

E) 40

Rpta. : "C"

PREGUNTA 4 :

En un paralelogramo, la longitud de un lado, es el triple de la longitud del otro lado, encontrar la longitud del mayor lado, si el perímetro del paralelogramo es 80.

A) 20

B) 30

C) 40

D) 50

E) 10

Rpta. : "B"

PREGUNTA 5 :

Las medidas de dos ángulos consecutivos de un paralelogramo se encuentran en la razón de 4 a 5. Encontrar la medida del menor ángulo.

A) 80°

B) 100°

C) 90°

D) 45°

E) 20°

Rpta. : "A"

PREGUNTA 6 :

Uno de los ángulos interiores de un trapecio isósceles mide 45°, su base menor mide 6 y la altura del trapecio mide 4. Calcular la longitud de la base mayor.

A) 10

B) 12

C) 14

D) 18

E) 20

Rpta. : "C"

PREGUNTA 7 :

Encontrar la relación de las bases de un trapecio, la relación de la mediana y del segmento que une los puntos medios de las diagonales es de 3 a 2. En un trapecio isósceles, sus lados no paralelos y su base menor son congruentes, si la medida de uno de los ángulos interiores es 60° y la base mayor mide 12. Encontrar la longitud de la base menor.

A) 4

B) 6

C) 7

D) 8

E) 10

Rpta. : "E"

PREGUNTA 8 :

El lado de un cuadrado es el cuádruplo del lado de un rombo, la suma de los perímetros de los dos cuadriláteros es 80. Encontrar el perímetro del cuadrado.

A) 20

B) 32

C) 40

D) 42

E) 64

Rpta. : "B"

PREGUNTA 9 :

Las bases de un trapecio miden 6 y 14, los ángulos adyacentes a la base mayor son complementarios. Hallar el segmento que une los puntos medios de las bases.

A) 2

B) 3

C) 4

D) 5

E) 6

Rpta. : "E"

PREGUNTA 10 :

La suma de las distancias de los vértices de un paralelogramo a una recta exterior es 84. Calcular la distancia del centro del paralelogramo a la recta exterior.

A) 41

B) 28

C) 18

D) 21

E) 24

Rpta. : "C"

PREGUNTA 11 :

Dado un terreno cuadrangular , cuyas diagonales miden 80m y 100m respectivamente ; se pregunta el propietario del mismo por la magnitud del perímetro y este contesta que no recuerda bien si la longitud es 370 ó 380. lo más probable , es :

A) 380m

B) 370m

C) 220m

D) 160m

E) 420m

Rpta. : "C"

PREGUNTA 12 :

Marca verdadero (V) o falso (F), según corresponda:

• El rombo es el paralelogramo que tiene todos sus ángulos internos iguales ...( )

• El cuadrado presenta todos sus ángulos internos de igual medida ...( )

• En todo paralelogramo, sus ángulos opuestos son de igual medida ...( )

• El romboide es un paralelogramo equilátero ...( )

PREGUNTA 13 :

Marca verdadero (V) o falso (F), según corresponda.

• Un romboide es un paralelogramo equilátero ...( )

• En un trapezoide convexo, la suma de sus ángulos internos es 540º ...( )

• Un rombo es un paralelogramo de lados iguales ...( )

• En todo cuadrilátero, la suma de ángulos internos es 360º ...( )

PREGUNTA 14 :

Calcula la medida del lado menor de un rectángulo, si es 5 cm menor que el lado mayor y además su perímetro es 50 cm.

PROBLEMAS RESUELTOS

PREGUNTA 1 :

En un paralelogramo de lados 6 y 16, la distancia entre los lados menores es 8. Calcule la distancia entre los lados mayores.

A) 1

B) 3

C) 5

D) 4

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 2 :

En un paralelogramo ABCD, AB=5 y BC=16. Si P es el punto de intersección de las bisectrices interiores de los ángulos B y C, calcule la distancia del punto P al punto medio del lado BC.

A) 2

B) 4

C) 6

D) 8

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 3 :

En el gráfico, AB=BL=LP=PC y AD=DL=LQ=QC. Calcule: x+y

A) 50º

B) 30º

C) 40º

D) 60º

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 4 :

A) 15°

B) 20°

C) 30°

D) 35°

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 5 :

Se tiene un trapecio ABCD cuyas diagonales se cortan perpendicularmente; si la base mayor AD es igual a la diagonal AC e igual a 4 cm. Calcular la longitud de la base menor BC , BD= 3 cm.

A) 1 cm

B) 2 cm

C) 3 cm

D) 4 cm

E) 5 cm

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 6 :

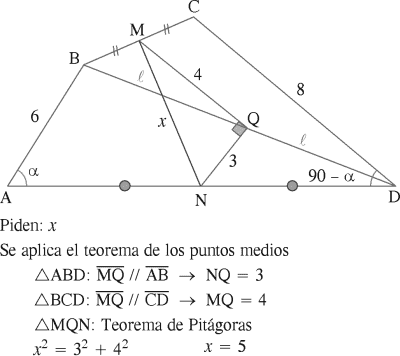
En un trapecio se cumple que el segmento que une los puntos medios de las diagonales y la mediana están en relación de 3 a 5. Calcule la relación de sus bases.

A) 1

B) 2

C) 3

D) 4

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 7 :

En un romboide ABCD; AB=12m, BC=16m . Se traza la bisectriz interior del ángulo A, la cual intersecta a BC en E y a la prolongación de DC en F; si se traza desde M punto medio de EF un rayo paralelo a CD, interceptado a AD en N. Hallar la longitud del segmento MN .

A) 12 cm

B) 20 cm

C) 18 cm

D) 14 cm

E) 16 cm

RESOLUCIÓN :