RUTAS Y TRAYECTORIAS EJERCICIOS RESUELTOS PDF RAZONAMIENTO MÁTEMÁTICO
PREGUNTA 1 :
La siguiente figura representa una red de caminos. Recorriendo solamente las líneas, ¿cuántas rutas diferentes existen para ir desde el punto A hacia el punto B sin pasar dos veces por el mismo punto?
A) 16
B) 30
C) 28
D) 24
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 2:
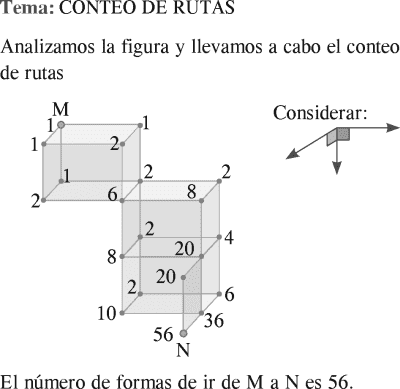
La siguiente figura representa una estructura de alambre. Recorriendo solo por las líneas en las direcciones indicadas, ¿de cuántas maneras diferentes se puede ir desde el punto M hasta el punto N?
A) 64
B) 50
C) 48
D) 56
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 3 :
En la figura, las líneas representan caminos. ¿Cuántas rutas distintas existen para ir desde el punto P hasta el punto Q, sin pasar en ningún momento dos veces por un mismo punto? Dé como respuesta la suma de las cifras de dicho resultado.
A) 15
B) 27
C) 12
D) 18
E) 9
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 4 :
En la siguiente figura, recorriendo solo por las líneas en las direcciones indicadas, solo hacia la derecha o hacia abajo, ¿de cuántas maneras diferentes se puede ir desde el punto A hasta el punto B?
A) 8400
B) 9600
C) 7200
D) 8200
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 5 :
En la figura adjunta, recorriendo solamente los segmentos hacia arriba, a la izquierda y en diagonales hacia arriba, ¿cuántas rutas diferentes existen para ir desde el punto B hasta el punto A?
A) 63
B) 39
C) 48
D) 52
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 6:
En la figura, recorriendo solamente por los segmentos, hacia la derecha o hacia abajo, ¿cuántas rutas diferentes existen para ir desde A hasta B?
A) 160
B) 164
C) 174
D) 171
E) 182
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 7 :
¿Cuántas rutas distintas existen para ir desde el punto A hacia el punto B sino se puede pasar por el punto C y además para ir del punto A al punto B siempre debe ir avanzando?
.png)
A) 482
B) 408
C) 312
D) 324
Rpta. : "C"
PREGUNTA 8 :
En la figura, recorriendo solamente por los segmentos, hacia la derecha o hacia abajo, ¿cuántas rutas distintas existen para ir desde el punto A al punto P, pasando por los puntos R y S?
.png)
A) 1400
B) 1320
C) 1200
D) 1520
Rpta. : "A"
PREGUNTA 9 :
En la figura, recorriendo solamente por los segmentos hacia la derecha o hacia abajo, ¿cuántas rutas distintas existen desde el punto M al punto S pasando siempre por los puntos P, Q y R?
.png)
A) 86
B) 20
C) 24
D) 44
Rpta. : "C"
PREGUNTA 10 :
Recorriendo solamente por los segmentos hacia la derecha, hacia abajo o descendiendo por la diagonal, ¿cuántas rutas distintas existen desde el punto P al punto Q?
.png)
A) 48
B) 59
C) 60
D) 71
Rpta. : "B"
PREGUNTA 11 :
En la figura cada línea representa un camino para unir dos puntos. ¿De cuántas maneras diferentes se puede ir de M hasta N sin pasar en ningún momento mas de una vez por el mismo tramo?
.png)
A) 108
B) 81
C) 72
D) 96
Rpta. : "B"
PREGUNTA 12 :
La figura muestra un octaedro construido con 12 segmentos de igual longitud. Recorriendo solamente por los segmentos de las aristas del octaedro y sin pasar dos veces por el mismo punto, ¿cuántas rutas distintas existen desde el punto P al punto Q?
.png)
A) 25
B) 20
C) 42
D) 28
Rpta. : "D"
PREGUNTA 13 :
Si no está permitido pasar por un mismo punto dos veces y recorriendo por las líneas de la figura, ¿cuántos caminos llevan de A a B?
.png)
A) 28
B) 26
C) 24
D) 22
Rpta. : "C"
PREGUNTA 14 :
En la figura, las líneas representan caminos. Calcule de cuántas maneras distintas se puede ir de A hasta B sin retroceder en ningún momento y luego volver hasta A por un camino que no sea el mismo que se utilizó en la ida.
.png)
A) 380
B) 500
C) 300
D) 460
Rpta. : "A"
OBJETIVOS
☛ Aplicar correctamente los principios y técnicas de conteo .
☛ Interpretar y comprender los diferentes gráficos.
☛ Comprender el concepto de caminos o rutas.
En este capítulo se trata de contar cuántas rutas o caminos distintos existen desde un punto inicial hasta un punto final. Se presentan ejercicios con rutas ya establecidas donde en la mayoría de los casos aplicar un método aditivo es suficiente para hallar el total de caminos existentes y en otros ejercicios donde las rutas no estarán preestablecidas , se tendrán que descubrir , bajo ciertas condiciones que se brinden , como el de no repetir un vértice o el de no repetir algún tramo , el total de rutas existentes
