DADOS Y DOMINOS EJERCICIOS RESUELTOS PDF RAZONAMIENTO MÁTEMÁTICO LÓGICA RECREATIVA

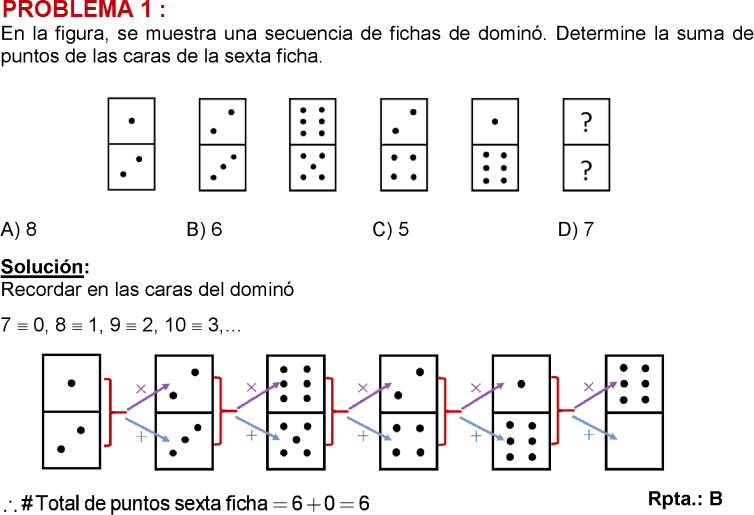
PREGUNTA 1 : 

Al lanzar cuatro dados normales, se ha obtenido en sus caras superiores, puntajes diferentes, tal que la suma de estos es 17. Si después se retira un dado ¿cuál sería el mayor puntaje total, que se obtendrá en las caras ocultas, de los tres dados que quedarían? 

A) 12 

B) 13 

C) 10 

D) 11 

RESOLUCIÓN :

La única posibilidad será: 6+5+4+2=17 

Las caras opuestas serán: 1+2+3=5 

# Puntaje máximo 3 dados cara opuesta 2+3+5=10 

Rpta. : "C"

PREGUNTA 2 :  

Halla el número de puntos no visibles en: 

a) 26 

b) 38 

c) 36 

d) 32 

e) 44 

RESOLUCIÓN :

Rpta. : "C"

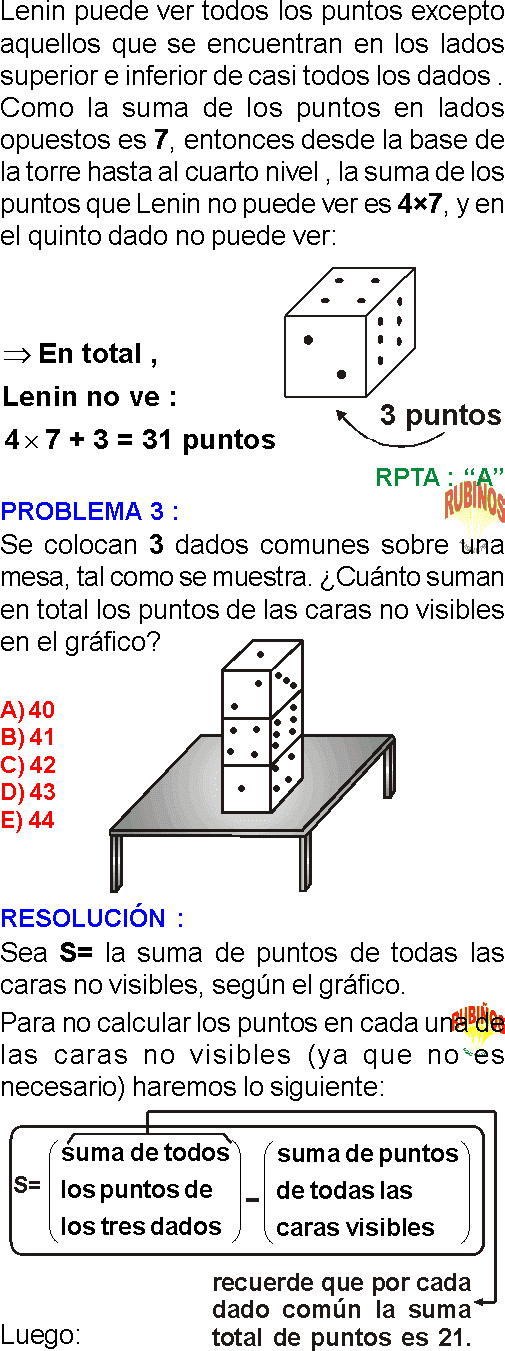
PREGUNTA 3 : 

A) 25 

B) 20 

C) 40 

D) 15 

E) 36 

RESOLUCIÓN :

Rpta. : "B"

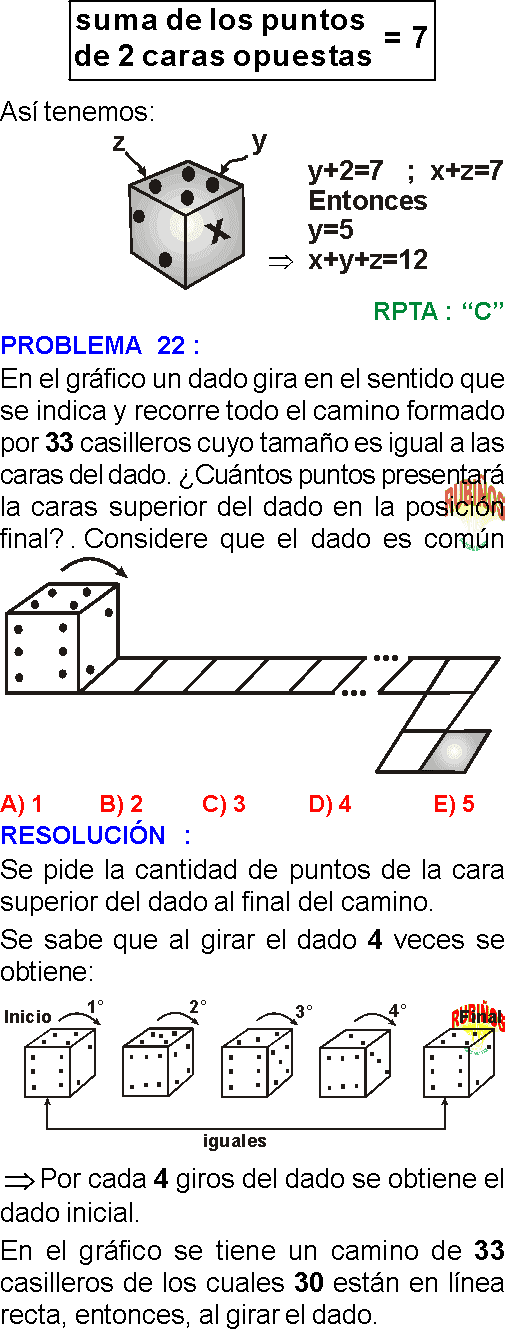
PREGUNTA 4 :

Se hacen rodar dos dados convencionales idénticos sin deslizarse sobre las casillas cuadradas (idénticas a las caras de los dados), tal como se muestra en la figura. Si los dados inician simultáneamente su rodamiento con la misma rapidez, determine la suma del número de puntos ubicados en la cara superior cuando los dados ocupen la casilla sombreada. 

A) 6 

B) 5 

C) 4 

D) 3 

E) 7 

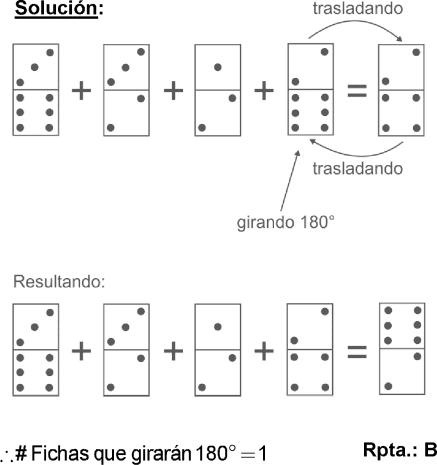
RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 5 :

Valeria y su hermano Nicolás están jugando con un dado convencional. Ella lanza el dado cinco veces y obtiene como suma de los puntos de la cara superior un número cuadrado perfecto de dos cifras. Nicolás lanza el dado cuatro veces y obtiene como suma de los puntos de la cara superior un número cubo perfecto de una cifra. ¿Cuál será la diferencia entre el máximo número de puntos que pudo obtener Nicolás en uno de sus lanzamientos y el mínimo número de puntos que pudo obtener Valeria en uno de sus lanzamientos? 

A) 3 

B) 4 

C) 2 

D) 1 

E) 5 

RESOLUCIÓN :

Y como piden la diferencia entre el máximo número de puntos que pudo obtener Nicolás en uno de sus lanzamientos y el mínimo número de puntos que pudo obtener Valeria en uno de sus lanzamientos: 5 – 1 = 4

Rpta. : "B"

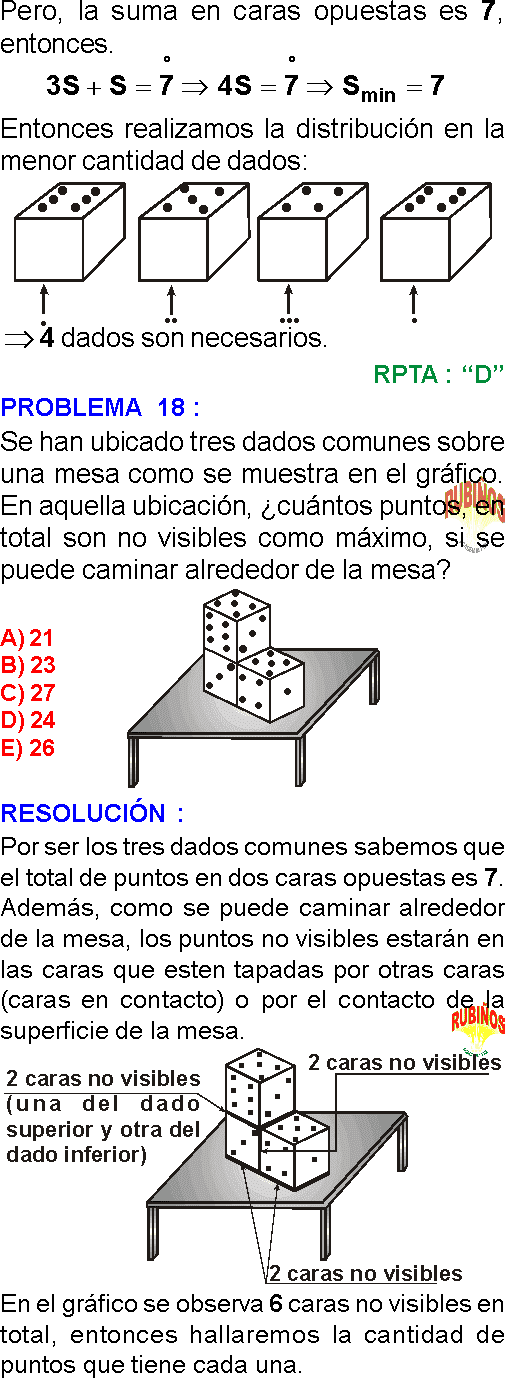
PREGUNTA 6 : 

¿Cuántos dados, como mínimo, se deben colocar sobre la mesa para que la suma de los puntos de sus caras superiores sea el triple de la suma de los puntos de sus caras inferiores? 

A) 1 

B) 2 

C) 3 

D) 4 

E) 5 

Rpta. : "D"

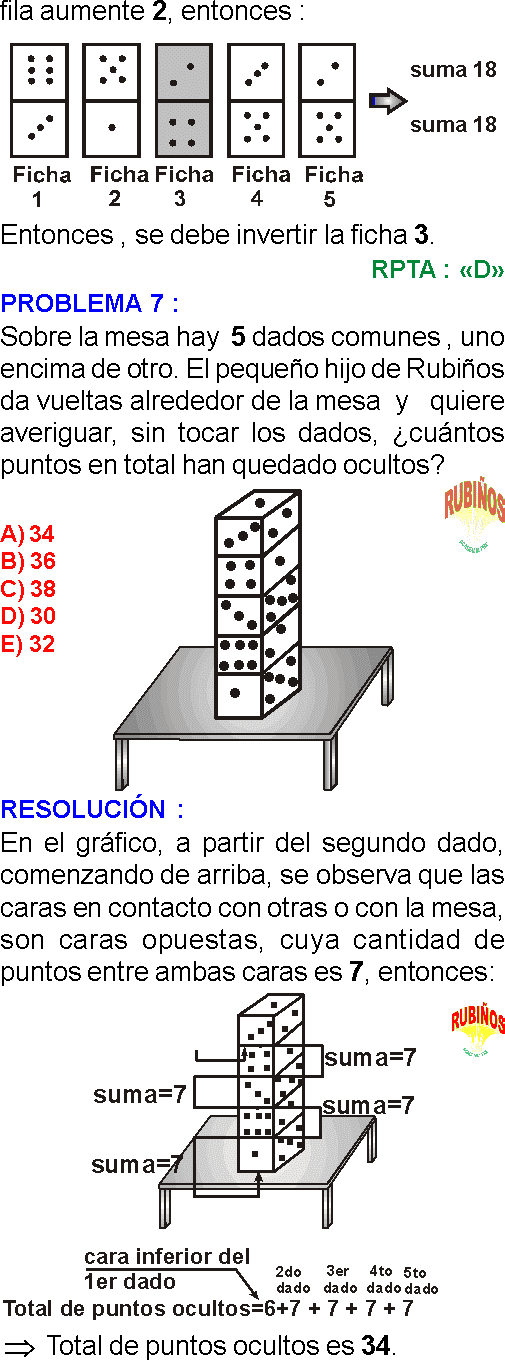
PREGUNTA 7 : 

Se tiene un dado no común en cuyas caras aparecen los números del 1 al 6. Al observar simultáneamente tres de sus caras de todas las formas posibles se obtienen los números del 7 al 14, como suma de puntos. Además, no hay dos caras opuestas con suma de puntos mayor a 9. Si al lanzar tres veces dicho dado se obtuvo 17 como suma de puntos de las caras superiores, ¿cuál fue la suma de los puntos de las caras inferiores? 

A) 7 

B) 8 

C) 9 

D) 10 

E) 6 

Rpta. : "C"