PRODUCTO VECTORIAL – PRODUCTO ESCALAR EJERCICIOS RESUELTOS – PRODUCTO DE VECTORES PDF – PRODUCTO CRUZ MIXTO
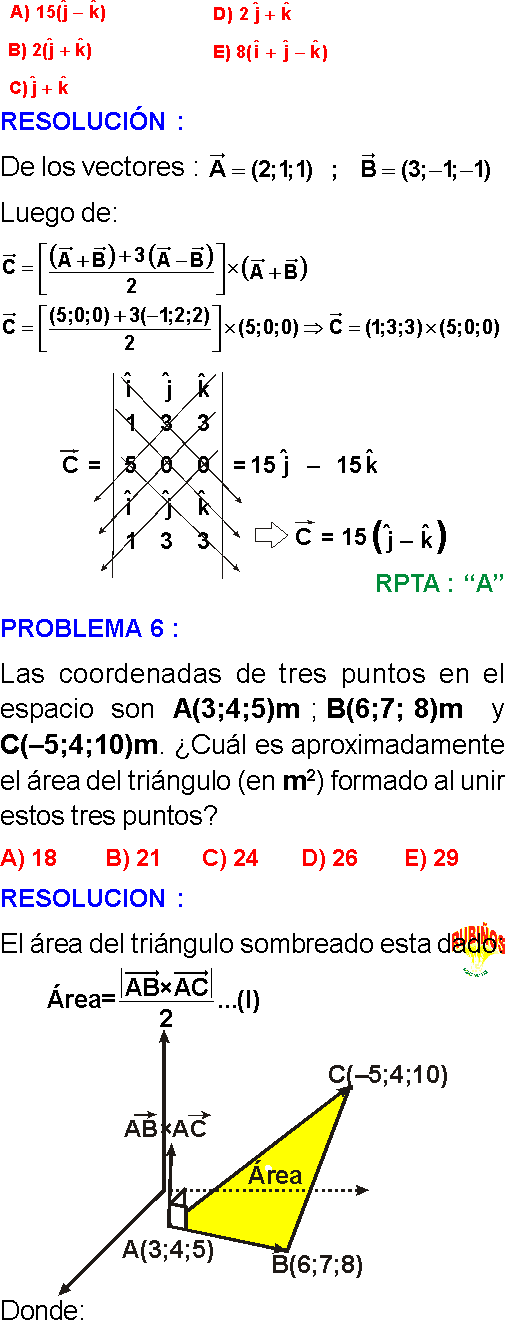
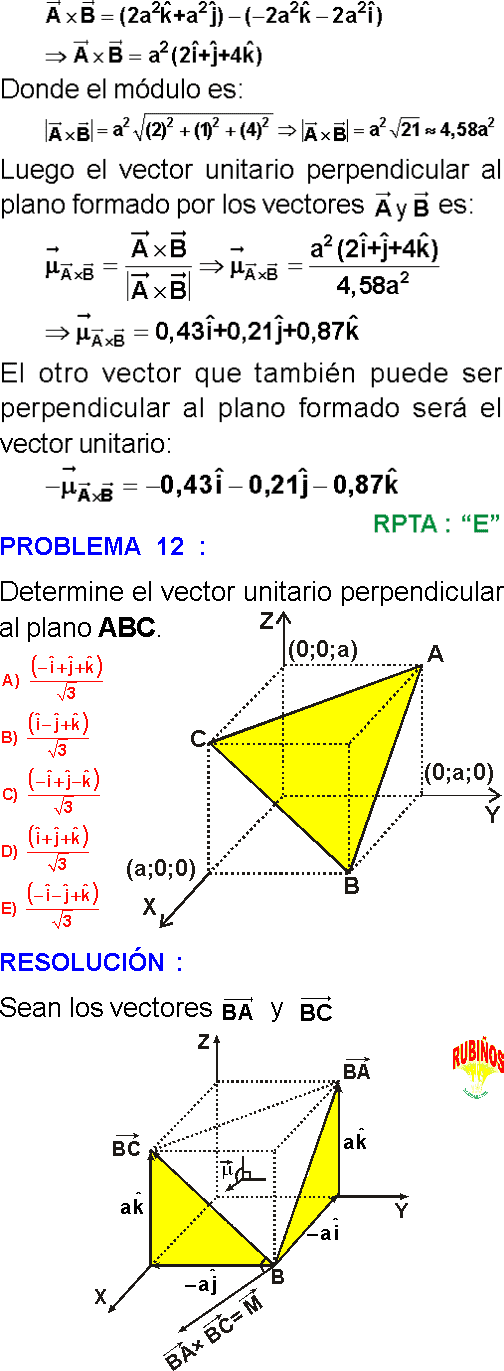
EJERCICIO 1
Las magnitudes vectoriales son importantes en muchos aspectos de la ciencia. Algunas veces se requiere establecer un vector perpendicular a algún plano determinado. Suponga que este plano contiene a los vectores concurrentes
Halle el vector unitario de un vector perpendicular a este plano.
MULTIPLICACIÓN DE VECTORES
En el álgebra vectorial se definen dos formas para realizar el producto de vectores: una es el producto escalar y la otra es el producto vectorial.
PRODUCTO ESCALAR
Es una operación en la cual al multiplicar escalarmente dos vectores, el resultado es una cantidad escalar.
Muchas magnitudes físicas resultan del producto escalar de dos magnitudes vectoriales.
Por ejemplo, la cantidad de trabajo mecánico
PRODUCTO VECTORIAL
Es una operación en la cual al multiplicar: vectorialmente dos vectores, el resultado es otro vector.
Si se conoce el módulo de cada vector y el ángulo que forman los vectores entre sí.
El producto vectorial entre dos vectores es un vector perpendicular a ambos vectores en la dirección dada por la regla de la mano derecha .
Si se cambia el orden de los vectores en el producto vectorial, se invierte el sentido del vector.
Notamos que el resultado del producto vectorial es otro vector, el cual es perpendicular al plano formado
☛ Producto escalar de dos vectores libres
☛ Producto vectorial de dos vectores libres
☛ Producto mixto de 3 vectores libres
☛ Aplicaciones
☛ Aplicaciones con vectores
☛ Módulo y vector unitario
☛ Ángulo de dos vectores.
☛ Vectores perpendiculares
☛ Vector normal a un plano y director de una recta
☛ Ángulo entre elementos del espacio
☛ Ángulo entre dos rectas
☛ Ángulo entre dos planos
☛ Ángulo ente un plano y una recta
☛ Distancias entre elementos del espacio
☛ Proyecciones
☛ Proyección de un punto sobre un plano
☛ Proyección de un punto sobre una recta
☛ Proyección de una recta sobre un plano
☛ Elementos simétricos
☛ Rectas que se apoyan sobre otras dos rectas
☛ Cálculo de áreas y volúmenes
VECTORES PARALELOS
Se dice que dos vectores son paralelos si y sólo si uno de los vectores es múltiplo escalar del otro.
Una interpretación geométrica del producto punto se obtiene a partir de la proyección escalar de un vector sobre otro.
En el curso anterior se estudió ya la definición de producto escalar para vectores en el plano, en éste lo extenderemos al espacio (si la tercera coordenada de los vectores es nula podemos particularizar al producto escalar en el plano).
Si recuerdas, en Física el trabajo realizado al desplazar una masa es igual al producto escalar de la fuerza y el desplazamiento
Propiedades del producto escalar de dos vectores:
☛ El producto escalar de un vector por sí mismo es igual al cuadrado del módulo
☛ El producto escalar es conmutativo
☛ El producto escalar es distributivo respecto a la suma de vectores
☛ El producto escalar de dos vectores es nulo si y sólo si son perpendiculares o alguno de los vectores es cero
INTERPRETACIÓN GEOMÉTRICA DEL PRODUCTO ESCALAR
Se puede relacionar geométricamente el producto escalar de dos vectores con la proyección de un vector sobre el otro
EXPRESIÓN ANALÍTICA DEL PRODUCTO ESCALAR
A partir de la propiedad distributiva del producto escalar y del producto escalar de los vectores unitarios, podemos obtener la expresión analítica del producto escalar de dos vectores cualesquiera.
Veamos primero el producto escalar de los vectores unitarios
PROPIEDADES DEL PRODUCTO VECTORIAL:
☛ El producto vectorial es anticonmutativo.
El módulo y la dirección no cambian, pero el sentido es el opuesto (ver regla sacacorchos).
☛ El producto vectorial es distributivo con la suma
INTERPRETACIÓN GEOMÉTRICA DEL PRODUCTO VECTORIAL
el área del paralelogramo es igual al módulo del producto vectorial de los dos vectores que lo forman
INTERPRETACIÓN GEOMÉTRICA DEL PRODUCTO MIXTO
Consideremos los tres vectores u v w aplicados sobre el mismo origen, de manera que formen un paralelepípedo (con sus proyecciones). Se cumple que el volumen del paralelepípedo es igual al valor absoluto del producto mixto de los tres vectores que lo forman
EXPRESIÓN ANALÍTICA DEL PRODUCTO MIXTO
Aplicando la expresión analítica del producto vectorial y escalar de los apartados anteriores, es fácil ver como el producto mixto se puede poner a partir del siguiente determinante