DIVISIÓN ARITMÉTICA EJERCICIOS RESUELTOS PDF
APRENDIZAJES ESPERADOS
☛ El presente estudio nos permite reforzar la operación de la división.
☛ Conocer las clases de división y las propiedades de la división inexacta.
La multiplicación y la división están estrechamente relacionadas ya que la división es la operación inversa de la multiplicación, de la misma forma que la adición y la sustracción.
Para dividir números enteros, dividimos los números y los signos según la regla.
¿Qué es la división aritmética?
Es aquella operación que consiste en saber cuántas veces un número llamado dividendo contiene a otro número menor o igual llamado divisor y a cuya cantidad de veces que lo contiene se le denomina cociente.
PROPIEDADES DE LA DIVISIÓN INEXACTA
𝑖) El residuo mínimo es igual a la unidad y el residuo máximo es igual al divisor disminuido en 1.
𝑖𝑖) El cociente por exceso es igual al cociente por defecto aumentado en 1.
𝑖𝑖𝑖) La suma de los residuos por defecto y por exceso es igual al divisor.
• Cuando en un problema solo hace referencia a la división inexacta, se asume división inexacta por defecto.
• Cuando en una división inexacta solo se indica residuo se refiere al residuo por defecto.
• Cuando en una división inexacta solo se indica cociente se refiere al cociente por defecto.
PRACTICA NIVEL BÁSICO
EJERCICIO 1 :
Al efectuar la división de 234 y 93, indicar la suma del residuo y el cociente.
A) 57
B) 59
C) 60
D) 62
E) 63
Rpta. : "B"
EJERCICIO 2 :
Al efectuar la división de 431 y 73, indicar la suma del residuo y cociente por exceso.
A) 71
B) 13
C) 70
D) 12
E) 11
Rpta. : "B"
EJERCICIO 3 :
En una división el residuo por defecto es 7 y el exceso es 13, el cociente es la mitad del divisor, calcular el dividendo.
A) 200
B) 207
C) 213
D) 193
E) 187
Rpta. : "B"
EJERCICIO 4 :
Si el residuo por exceso es 13, el divisor 30, el cociente por exceso es 2/5 del divisor, calcular el dividendo.
A) 360
B) 373
C) 347
D) 350
E) 340
Rpta. : "C"
EJERCICIO 5 :
En una división el divisor termina en ..... 41; el cociente en .... 15 y el residuo termina en .... 12, entonces el dividendo termina en:
A) 23
B) 24
C) 25
D) 27
E) 28
Rpta. : "D"
EJERCICIO 6 :
Dividir el mayor número capicúa de tres cifras diferentes entre el menor capicúa de tres cifras diferentes, indicar el complemento aritmético del residuo por exceso.
A) 21
B) 80
C) 20
D) 79
E) 78
Rpta. : "D"
EJERCICIO 7 :
La suma de dos números es 43; al dividirlos su cociente es 2 y el residuo 7, calcular el número mayor.
A) 31
B) 30
C) 32
D) 33
E) 29
Rpta. : "A"
EJERCICIO 8 :
La suma de los términos de una división entera exacta es 39. Si el dividendo es nueve veces el divisor, ¿cuál es el dividendo?
A) 12
B) 27
C) 24
D) 26
E) 36
Rpta. : "B"
PRACTICA PROPUESTA
EJERCICIO 1 :
Halla el dividendo de una división por defecto si el divisor es 31, el cociente 12 y el residuo 7
A) 379
B) 362
C) 327
D) 351
E) 328
Rpta. : "A"
EJERCICIO 2 :
Halla el dividendo de una división por defecto si el divisor es 47, el cociente 9 y el residuo es lo máximo posible
A) 401
B) 412
C) 469
D) 471
E) 482
Rpta. : "C"
EJERCICIO 3 :
Halla el dividendo de una división por exceso si el divisor es 24, el cociente 16 y el residuo 8.
A) 304
B) 376
C) 353
D) 350
E) 399
Rpta. : "B"
EJERCICIO 4 :
Halla el dividendo de una división por exceso si el divisor es 76, el cociente la mitad del divisor y el residuo el menor posible.
A) 1457
B) 3714
C) 2788
D) 2887
E) 2328
Rpta. : "D"
EJERCICIO 5 :
Halla el dividendo de una división por defecto si el residuo máximo es 56, y el cociente es la tercera parte del divisor.
A) 1402
B) 1139
C) 1024
D) 1351
E) 1301
Rpta. : "B"
PROBLEMA 6 :
Al efectuar una división se obtiene 4 de cociente y 3 de residuo; al agregar 4 unidades al dividendo; el cociente aumenta en 1 y no queda residuo. Hallar el dividendo.
A) 24
B) 32
C) 31
D) 43
E) 57
Rpta. : "C"
PROBLEMA 7 :
Al sumar dividendo y divisor resulta 21 veces el residuo y al restarlo resulta 11 veces el residuo, hallar el cociente.
A) 1
B) 3
C) 5
D) 2
E) 4
Rpta. : "B"
PROBLEMA 8 :
Un número natural N se divide entre 15, por defecto y por exceso, observándose que: el resto por exceso es mínimo y el cociente por defecto igual a 3. Calcular la suma de cifras de N.
A) 10
B) 11
C) 12
D) 13
E) 14
Rpta. : "E"
PROBLEMA 9 :
Al dividir N entre 481 se obtuvo un cociente entero positivo que es la quinta parte del residuo. ¿Cuántos valores puede tomar N?
A) 480
B) 95
C) 96
D) 192
E) más de 500
Rpta. : "C"
PROBLEMA 10 :
El dividendo en una división entera es un número de 3 cifras, el divisor es el complemento aritmético del dividendo, el cociente es 65 y la razón aritmética del divisor y el resto es 5; calcular la suma de cifras del dividendo.
A) 18
B) 19
C) 20
D) 21
E) 22
Rpta. : "E"
PROBLEMA 11 :
Al dividir N entre 30 el cociente termina en 12 y el residuo es máximo, calcule la suma de las tres últimas cifras de N.
A) 17
B) 18
C) 19
D) 20
E) 21
Rpta. : "D"
PROBLEMA 12 :
En una división inexacta el dividendo es 2604, el divisor es una vez más que el cociente y el cociente es dos veces más que el residuo. Calcule la suma de los términos de la división.
A) 2676
B) 2712
C) 2684
D) 2718
E) 2724
Rpta. : "E"
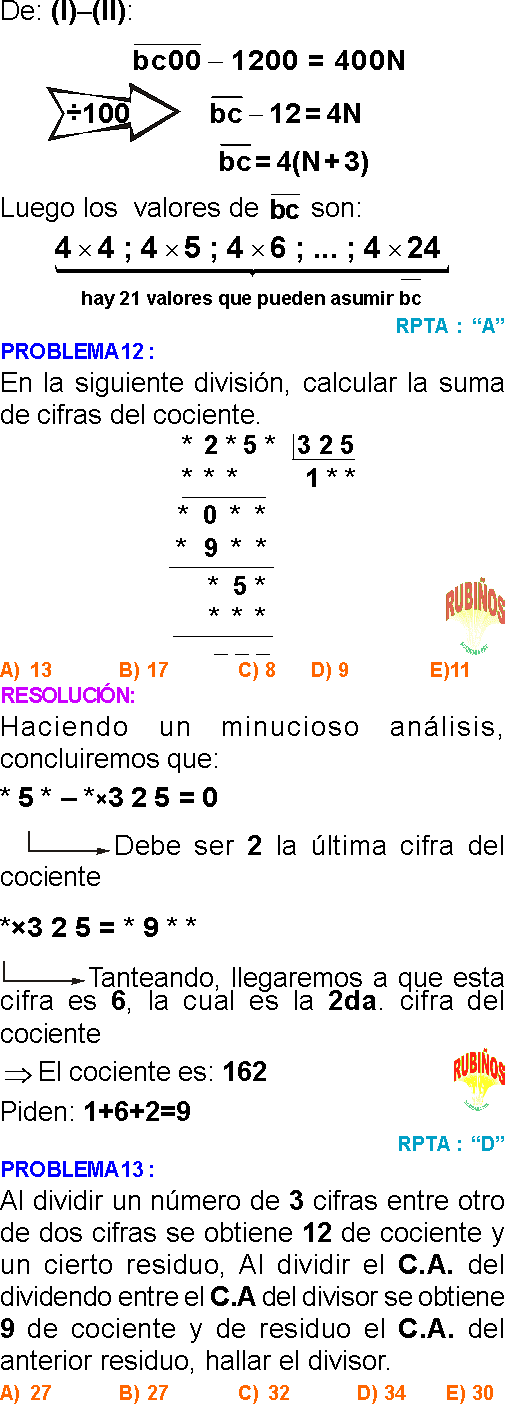
PROBLEMA 13 :
Al dividir un número de 3 cifras entre otro de dos cifras se obtiene 12 de cociente y un cierto residuo, Al dividir el C.A. del dividendo entre el C.A del divisor se obtiene 9 de cociente y de residuo el C.A. del anterior residuo, hallar el divisor.
A) 27
B) 27
C) 32
D) 34
E) 30
Rpta. : "E"
PROBLEMA 14 :
En una división de términos enteros, la suma de los cuatro términos es 271. Si se multiplica al dividendo y divisor por 4, la suma de términos sería 1030. Halle el dividendo.
A) 127
B) 203
C) 237
D) 243
E) 224
Rpta. : "C"
PROBLEMA 15 :
La suma de los cuatro términos de una división es 1079. Si se multiplica el dividendo y el divisor por 3 y se vuelve a realizar la división, la suma de los nuevos términos es 3185. Calcule el dividendo original.
A) 912
B) 985
C) 983
D) 989
E) 812
Rpta. : "D"
PROBLEMA 16 :
El cociente y el residuo de una división inexacta son 37 y 19 respectivamente. Si se le aumenta al dividendo 157 y se vuelve a dividir, el cociente aumenta en 8 y el residuo disminuye en 11. Determinar la suma de cifras del dividendo inicial.
A) 22
B) 13
C) 18
D) 17
E) 9
Rpta. : "A"
PROBLEMA 17 :
Al dividir un número capicúa de 3 cifras se obtiene de cociente un número capicúa de 2 cifras. Si además el producto de los residuos por defecto y exceso es 72. Determinar el producto de las cifras del mayor dividendo dado que el residuo por defecto es 9.
A) 96
B) 245
C) 150
D) 200
E) 576
Rpta. : "B"
PROBLEMA 18 :
Se divide un número de cuatro cifras entre otro de dos cifras, obteniéndose como cociente 181, y como residuos parciales a 17; 2 y 5 respectivamente . Determinar la suma de cifras del mayor dividendo posible.
A) 20
B) 27
C) 31
D) 28
E) 32
Rpta. : "B"
PROBLEMA 19 :
Se realiza la división de los números 4609 y 218. ¿Cuántos números pueden sumarse al dividendo, de tal manera que el nuevo cociente sea 23?
A) 213
B) 215
C) 225
D) 218
E) 220
Rpta. : "D"
PROBLEMA 20 :
En una división inexacta, el dividendo termina en 95, el cociente en 87 y el residuo en 72. Halle la suma de las dos últimas cifras del divisor.
A) 10
B) 9
C) 8
D) 11
E) 12
Rpta. : "D"
DIVISIÓN
Es una operación inversa a la multiplicación que consiste en que dados dos números enteros llamados dividendo y divisor se obtiene un tercer número llamado cociente que nos indica el número de veces que contiene el dividendo al divisor.
La cantidad de unidades que se posee , la cual se va agrupar se denomina dividendo , al tamaño del grupo en el cual se esta agrupando el dividendo ; se denomina divisor y la cantidad de grupos obtenidos de denomina cociente , teniéndose como consecuencia que sobre o falte unidades , a la cual se denomina residuo.
DIVISIÓN ENTERA
Es aquella división donde todos sus términos son enteros , se clasifica en :
I) DIVISION EXACTA
Cuando al agrupar las unidades no sobra ni falta unidades , es decir , se considera residuo cero.
II) DIVISIÓN INEXACTA
Cuando al agrupar las unidades sobran o faltan unidades para formar un grupo más .
☛ Cuando sobra unidades se dice que la división es inexacta por defecto.
☛ Cuando falta unidades para formar un grupo más, se dice que la división es inexacta por exceso.
OBSERVACIONES
☛ Tanto el dividendo y el divisor en ambas divisiones son iguales.
☛ El cociente por exceso , en una unidad más en el cociente por defecto.
☛ Lo que sobra o falta unidades suman exactamente un grupo.
PROPIEDAD DE LA DIVISIÓN INEXACTA
(cero)<(residuo)<(divisor)
Cuando la división es inexacta , y no se específica el tipo , se asume que es inexacta por defecto.
LEYES FORMALES DE LA DIVISIÓN
I) LEY DE UNIFORMIDAD
Si se dividen miembro a miembro dos igualdades (con la segunda igualdad diferente de cero), el resultado es otra igualdad
II) LEY DEL INVERSO MULTIPLICATIVO
Para todo número N diferente de cero , existe uno y sólo un elemento denominado inverso multiplicativo
III) LEY DISTRIBUTIVA
El cociente de una suma o resta entre un número es igual a la suma o resta los cocientes de cada uno de los términos entre el número dado.
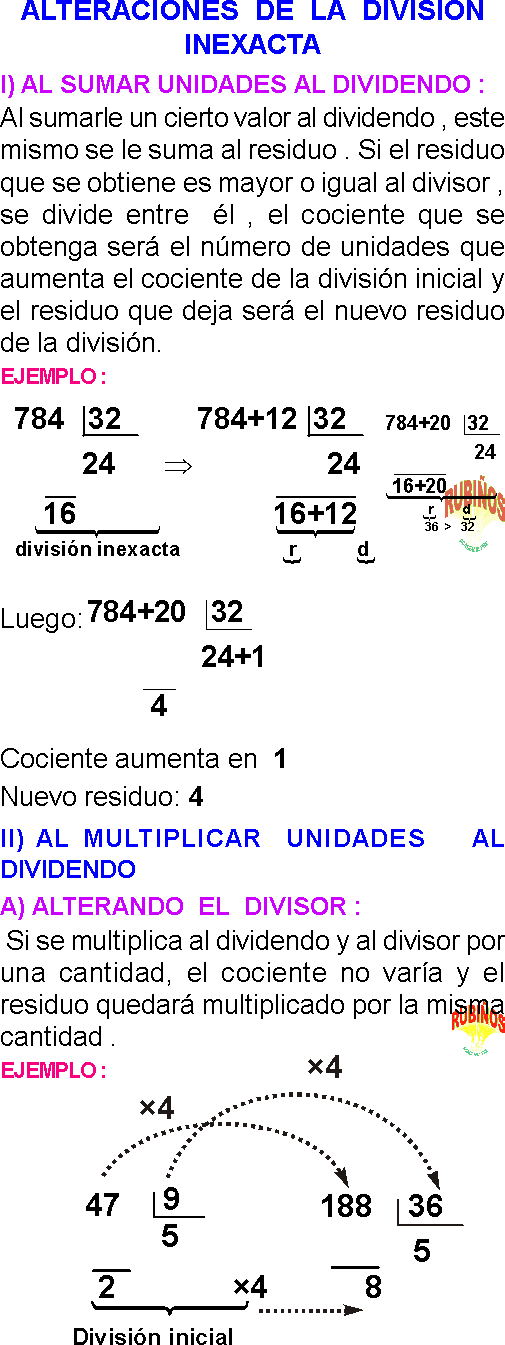
ALTERACIONES DE LA DIVISION INEXACTA
AL SUMAR UNIDADES AL DIVIDENDO
Al sumarle un cierto valor al dividendo , este mismo se le suma al residuo .
Si el residuo que se obtiene es mayor o igual al divisor , se divide entre él , el cociente que se obtenga será el número de unidades que aumenta el cociente de la división inicial y el residuo que deja será el nuevo residuo de la división.
AL MULTIPLICAR UNIDADES AL DIVIDENDO
A) ALTERANDO EL DIVISOR
Si se multiplica al dividendo y al divisor por una cantidad, el cociente no varía y el residuo quedará multiplicado por la misma cantidad .
ALTERANDO EL COCIENTE
Si se multiplica al dividendo y al cociente por una misma cantidad el residuo quedará multiplicado por la misma cantidad, teniendo en cuenta las observaciones del caso (I)
CANTIDAD DE CIFRAS DE UN COCIENTE
La cantidad de cifras del cociente de dos números, puede ser como mínimo igual a la diferencia entre las cantidades de cifras del dividendo y divisor; y como máximo la diferencia aumentada en una unidad.
CUANDO EL NÚMERADOR Y DENOMINADOR TIENEN VARIOS FACTORES
Primero se calcula la cantidad de cifras como máximo y como mínimo, tanto del numerador como denominador, mediante la regla del producto.
Luego para hallar el máximo del cociente se compara el máximo del numerador con el mínimo del denominador , análogamente para hallar el mínimo del cociente se compara, el mínimo del numerador con el máximo del denominador, ambos mediante la determinación de la cantidad de un cociente.