MATRICES EJERCICIOS RESUELTOS PDF
EJERCICIO 1 :
Dada las matrices:
Determina la traza de A+B
a) 4
b) 10
c) 8
d) 6
e) 12
RESOLUCIÓN :
.png)
Rpta. : "D"
EJERCICIO 2 :
Dada la matriz
.png)
halla la traza de aquella matriz B que sumada con la matriz A origina la matriz identidad.
A) 4
B) – 4
C) – 2
D) 5
E) 2
RESOLUCIÓN :
.png)
Rpta. : "B"
EJERCICIO 3 :
RESOLUCIÓN :
Rpta. : "A"
EJERCICIO 4 :
Considere las matrices de 2×2
Calcule la suma de los elementos de la matriz C=A6+B3
A) 1
B) 2
C) 3
D) 4
E) 5
RESOLUCIÓN :
Rpta. : "D"
Diagonal principal-Matriz diagonal
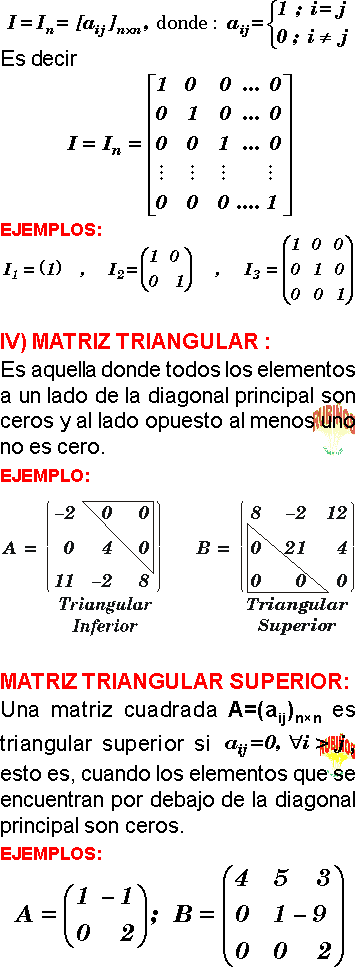
Matriz identidad
Matriz nula
Matriz triangular superior
Matriz simétrica
Traza de una matriz
Matriz transpuesta
Suma de matrices
Multiplicación escalar
Multiplicación de matrices
Determinante de una matriz
Matriz de menores
Matriz de cofactores
Matriz singular
Inversa de una matriz
SISTEMAS DE ECUACIONES SIMULTANEAS
Método Grafico (sistemas de 2x2)
ELIMINACIÓN GAUSIANA
METODO DE GAUSS JORDAN
SOLUCIÓN POR METODO DE CRAMER DEFINICIÓN Y DESCRIPCIÓN DE MATRICES
OPERACIONES CON MATRICES
MATRICES CUADRADAS
Definiciones en las matrices cuadradas
Tipos de matrices cuadradas
Matiz estrictamente triangular
Matriz diagonal
Matriz escalar
Matriz inversa
Matriz simétrica
Matriz antisimétrica
Propiedades de las matrices cuadradas
TRANSPUESTA DE UNA MATRIZ
DETERMINANTE DE UNA MATRIZ CUADRADA
Cálculo de un determinante
Método de Sarrus
Cálculo del determinante de orden n, por los adjuntos
Método del pivote o de Chio
Método triangularizante
CÁLCULO DE LA MATRIZ INVERSA DE UNA DADA
OPERACIONES ELEMENTALES
Operaciones elementales inversas
Matrices equivalentes por filas Definición de Matrices y tipos de Matrices
Operaciones con Matrices
Igualdad de Matrices
Suma de Matrices
Producto de una Matriz por un número (escalar)
Producto de Matrices
Transposición de Matrices. Matrices simétricas y antisimétricas
Matriz inversa
Definición.
Cálculo
Resolución de ecuaciones matriciales
OBJETIVOS:
* Valorar la importancia del álgebra matricial y la adquisición de estrategias para la simplificación de los cálculos.
* Identificar los tipos de matrices.
* Operar con matrices: suma y diferencia de matrices, producto de un número real por una matriz, producto de matrices. Conocer las propiedades de estas operaciones.
INTRODUCCIÓN:
Hablar de matrices hoy en día es hablar de una herramienta tan común en matemáticas, que con el tiempo apareció en forma independiente. La teoría de matrices y su proceso de formación fue a mediados del siglo pasado, pero su plenitud y elegancia la adquiere después. Hasta hoy la teoría de matrices es un instrumento de investigación apropiado a las necesidades prácticas y a las construccions abstractas de las matemáticas modernas. Si se conoce la naturaleza de una matriz, es posible valerse de ella en el almacenamiento, presentación y manipulación de datos. Si los datos se guardan dentro de una matriz con algún patrón lógico, la recuperación de los elementos individuales o grupos de elementos puede ser relativamente fácil. A menudo, se necesita manipular datos que se almacenan en una matriz. Por ejemplo las tablas del impuesto sobre la renta, las calificaciones obtenidas por un grupo de estudiantes, los informes económicos de una compañía , y muchos otros datos. En la actualidad, la principal utilidad de las matrices tiene que ver con aplicaciones computarizadas. Los programas de computación se valen periódicamente de matrices ‘‘arreglos’’ para guardar y procesar información. Las matrices surgen de un gran número de situaciones de la vida diaria. Por ejemplo, al considerar los cursos del POLITÉCNICO de tu zona y analizar el número de estudiantes por especialidad. Ejemplos Computadoras Se asigna a cada curso una fila y cada programa una columna.
De acuerdo con la tabla anterior se observa:
* Los cursos determinan 6 filas.
* Los programas de arquitectura, computadores, diseño industrial y electricidad, determinan 4 columnas.
* La intersección de una fila y una columna informa sobre el número de estudiantes de un curso que hay en el programa. Por ejemplo, el número colocado en la interseción de la quinta fila y la segunda columna indica que hay 36 estudiantes de décimo grado en el programa de computadoras. Las matrices aparecen por primera vez hacia el año 1850, introducidas por J.J. Sylvester El desarrollo inicial de la teoría se debe al matemático W.R. Hamilton en 1853 En 1858,A.Cayley introduce la notaciónmatricial como una forma abreviada de escribir un sistema de m ecuaciones lineales con n incógnitas. Las matrices se utilizan en el cálculo numérico, en la resolución de sistemas de ecuaciones lineales, de las ecuaciones diferenciales y de las derivadas parciales. Además de su utilidad para el estudio de sistemas de ecuaciones lineales, las matrices aparecen de forma natural en geometría, estadística, economía, informática, física, etc... La utilización de matrices (arrays) constituye actualmente una parte esencial de los lenguajes de programación, ya que la mayoría de los datos se introducción en los ordenadores como tablas organizadas en filas y columnas : hojas de cálculo, bases de datos,... MATRIZ Una matriz es un arreglo o disposición rectangular de números. Si el arreglo tiene m filas (horizontales) y n columnas (verticales), se llama matriz de orden m×n.
