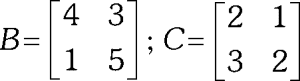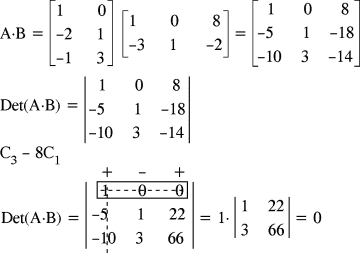DETERMINANTES EJERCICIOS RESUELTOS PDF
EJERCICIO 1 :
Calcula el determinante de A
Si A=2C–3B
Siendo
A) 110
B) 111
C) 109
D) 113
E) 112
RESOLUCIÓN :
Rpta. : "C"
EJERCICIO 2 :
Dado el siguiente sistema de ecuaciones:
2x+2y – 2z=0
2x – y+az=0
3x+y – z=0
Si este sistema de ecuaciones no tiene soluciones no nulas, entonces el valor de a pertenece al intervalo:
A) 〈∞;– 2〉
B) [– 2;0〉
C) [0;2〉
D) [2;4〉
E) [4; +∞〉
RESOLUCIÓN :
Rpta. : "C"
EJERCICIO 3 :
Dada la matriz A=(aij)m1×m1
Halla el determinante de la adjunta de A, si |A|=m2, donde m1 y m2 son raíces de la ecuación m2–m=20
A) 236
B) 252
C) 248
D) 250
E) 256
RESOLUCIÓN :
Rpta. : "E"
EJERCICIO 4 :
Sean las matrices
Calcule Det(A⋅B)
A) –2
B) –1
C) 0
D) 1
E) 2
RESOLUCIÓN :
Rpta. : "C"
EJERCICIO 5 :
RESOLUCIÓN :
Rpta. : "B"
EJERCICIO 6 :
Calcule la traza de A–1+B–1
siendo
A) 5/4
B) 7/4
C) 9/4
D) 11/4
E) 13/4
RESOLUCIÓN :
Rpta. : "D"
EJERCICIO 7 :
RESOLUCIÓN :
Rpta. : "B"
EJERCICIO 1 :
En un campeonato de fútbol, un equipo jugó quince partidos y sumó un total de veintisiete puntos. Si por cada partido ganado obtuvo tres puntos, por partido empatado un punto y por cada partido perdido cero puntos, además se sabe que los partidos empatados no fueron más de siete. Determine de cuántas formas puede obtener el equipo dicho puntaje.
A) 1
B) 3
C) 4
D) 2
E) 5
Rpta. : "B"
EJERCICIO 2 :
Los incrementos o decrementos de los precios en soles de tres productos M, N y P, de una semana a otra, fueron tales que la suma de las variaciones de sus precios es tres soles; la suma de la variación del precio del producto M con la del producto N excede en cinco soles a la variación del precio del producto P; el doble de la variación del precio de M más la variación del precio P excede en cuatro soles a la variación del precio de N. ¿Qué producto(os) sufrieron decrementos?
A) Todos
B) P
C) N y P
D) M y P
E) N
Rpta. : "B"
Conceptos previos, permutacionesDefinición general de determinantes
Determinante de matrices de orden 2 y orden 3.
Determinante matrices cuadradas de orden 2
Determinante matrices cuadradas de orden 3
Determinante de algunas matrices especiales
Propiedades de los determinantes
Otros métodos de calcular los determinantes. Determinante de matriz de orden 4
Por adjuntos
Haciendo cero una fila o una columna
Determinante de Vandermonde
Cálculo de la matriz inversa.
Rango de una matriz Determinantes
Determinantes de una matriz (2x2)
Determinantes de una matriz (3x3)
Determinantes de una matriz (nxn)
Propiedades de los determinantes
Cálculo de la matriz inversa
Método de cofactores
Matriz inversa por el método de cofactores
Solución de sistemas de ecuaciones utilizando matriz inversa
Método de expansión por cofactores
Regla de Cramer
OBJETIVOS : * Valorar la importancia de los determinantes, dentro del álgebra matricial. * Calcular el determinante de una matriz cuadrada de cualquier orden. * Conocer las propiedades de los determinantes y su contribución a la simplificación de los cálculos. * Conocer métodos para calcular los determinantes y la matriz inversa. * Calcular la inversa de una matriz cuadrada de orden 2 ó 3 por el método de Gauss. * Calcular el rango de una matriz por el método de Gauss. INTRODUCCIÓN : Existen diferentes formas de asignar a una matriz un número , o sea , de establecer una función cuyo dominio sea el conjunto de todas las matrices cuadradas. Una de estas funciones es la que se conoce como determinante de una matriz. El determinante de unamatriz cuadrada es un número muyútil en la teoría del álgebra lineal y se puede calcular de manera directa. Los determinantes fueron introducidos en Occidente a partir del siglo XVI, esto es, antes que las matrices, que no aparecieron hasta el siglo XIX. Conviene recordar que los chinos (Hui, Liu. iuzhang Suanshu o Los nueve capítulos del arte matemático.) fueron los primeros en utilizar la tabla de ceros y en aplicar un algoritmo que, desde el Siglo XIX, se conoce con el nombre de Eliminación gaussiana. En su sentido original, el determinante determina la unicidad de la solución de un sistema de ecuaciones lineales. Fue introducido para el caso de orden 2 por Cardano en 1545 en su obra Ars Magna presentado como una regla para la resolución de sistemas de dos ecuaciones con dos incógnitas. Esta primera fórmula lleva el nombre de regula de modo. La aparición de determinantes de órdenes superiores tardó aúnmás de cien años en llegar. Curiosamente el japonés Kowa Seki y el alemán Leibniz otorgaron los primeros ejemplos casi simultáneamente. Leibniz estudió los distintos tipos de sistemas de ecuaciones lineales. Al no disponer de la notación matricial, representaba los coeficientes de las incógnitas con una pareja de índices: así pues escribía ij para representar ai , j . En 1678 se interesó por un sistema de tres ecuaciones con tres incógnitas y obtuvo, para dicho ejemplo, la fórmula de desarrollo a lo largo de una columna. El mismo año, escribió un determinante de orden 4 , correcto en todo salvo en el signo. Leibniz no publicó este trabajo, que pareció quedar olvidado hasta que los resultados fueron redescubiertos de forma independiente cincuenta años más tarde. En elmismo periodo, Kowa Seki publicó unmanuscrito sobre los determinantes, donde se hallan fórmulas generales difíciles de interpretar. Parece que se dan fórmulas correctas para determinantes de tamaño 3 y 4, y de nuevo los signos mal para los determinantes de tamaño superior. El descubrimiento se queda sin futuro a causa del cierre de Japón al mundo exterior por órdenes del shMgun, lo que se ve reflejado en la expulsión de los Jesuitas en 1638. DETERMINANTES DE CUALQUIER DIMENSIÓN En 1748, un póstumo tratado de álgebra deMacLaurin recupera la teoría de los determinantes al contener la escritura correcta de la solución de un sistema de cuatro ecuaciones con cuatro incógnitas. En 1750, Cramer formula las reglas generales que permiten la resolución de un sistema de n ecuaciones con n incógnitas, aunque no ofrece demostración alguna. Los métodos de cálculo de los determinantes son hasta entonces delicados debido a que se basan en la noción de signatura de una permutación. Losmatemáticos se familiarizan con este nuevo objeto a través de los artículos de Bézout en 1764, de Vandermonde en 1771 (que proporciona concretamente el calculo del determinante de la actual Matriz de Vandermonde). En 1772, Laplace establece las reglas de recurrencia que llevan su nombre. En el año siguiente, Lagrange descubre la relación entre el cálculo de los determinantes y el de los volúmenes. Gauss utiliza por primera vez el término « determinante », en las Disquisitiones arithmeticae en 1801. Lo empleaba para lo que hoy día denominamos 361 discriminante de una cuádrica y que es un caso particular de determinantemoderno. Igualmente estuvo cerca de obtener el teorema del determinante de un producto. APARICIÓN DE LA NOCIÓN MODERNA DE DETERMINANTE Cauchy fue el primero en emplear el término determinante con su significadomoderno. Se encargó de realizar una síntesis de los conocimientos anteriores y publicó en 1812 la fórmula del determinante de un producto. Ese mismo año Binet ofreció una demostración para dicha fórmula. Paralelamente Cauchy establece las bases del estudio de la reducción de endomorfismos. Con la publicación de sus tres tratados sobre determinantes en 1841 en la revista Crelle, Jacobi aporta a la noción una gran notoriedad. Por primera vez presentamétodos sistemáticos de cálculo bajo una forma algorítmica. Del mismo modo, hace posible la evaluación del determinante de funciones con instauración del jacobiano. El cuadro matricial es introducido por los trabajos de Cayley y James Joseph Sylvester. Cayley es también el inventor de la notación de los determinantes mediante barras verticales y establece la fórmula para el cálculo de la inversa. La teoría se ve reforzada por el estudio de determinantes que tienen propiedades de simetría particulares y por la introducción del determinante en nuevos campos de las matemáticas, como el wronskiano en el caso de las ecuaciones diferenciales lineales. Para el cálculo de determinantes de matrices de cualquier orden, existe una regla recursiva (teorema de Laplace) que reduce el cálculo a sumas y restas de varios determinantes de un orden inferior. Este proceso se puede repetir tantas veces como sea necesario hasta reducir el problema al cálculo de múltiples determinantes de orden tan pequeño como se quiera. Sabiendo que el determinante de un escalar es el propio escalar, es posible calcular el determinante de cualquier matriz aplicando dicho teorema. - - - -
