RECTAS PLANOS PROBLEMAS PREUNIVERSITARIOS RESUELTOS de GEOMETRÍA DEL ESPACIO
Los temas tratados hasta ahora eran objeto de la geometría plana, sin embargo, en la realidad, la figura plana de dos dimensiones no existe como tal sino formando parte de un cuerpo del espacio.
Así, cuando manipulamos papel, cartón, madera, etc., lo hacemos con figuras tridimensionales, ya que éstas tienen un cierto grosor; sólo mentalmente separamos la figura plana de la del espacio, imaginándola aisladarnente como si no tuviera relación con los cuerpos sólidos.
En esta parte del libro estudiaremos las figuras cuyos elementos básicos están situados en el espacio, lo que constituye el objetivo de la geometría sólida o espacial.
No obstante, los conceptos dados en geometría plana son aplicables de cierto modo a la geometría espacial.
Por ello, dando por asumidas las ideas de punto, recta y plano vistas en la primera parte.
Analizaremos sus relaciones desde la óptica espacial, pues si bien en la geometría plana puntos y rectas se hallan dentro del plano, en la geometría espacial no sucede así, ya que en este caso los puntos y las rectas pueden ser exteriores a él.
GEOMETRÍA DEL ESPACIO O ESTEREOMETRÍA
Estudia la forma y extensión de las figuras geométricas cuyos puntos no están en un mismo plano (espacio tridimensional)
ESPACIO TRIDIMENSIONAL
A dicha idea tenemos dos postulados importante:
a. Dada una recta cualquiera L, hay por lo menos un punto P, tal que P no pertenece a L.
b. Dado un plano cualquiera M, hay por lo menos un punto P, tal que P no pertenece a M.
POSTULADOS DEL PLANO
a. Todo plano contiene al menos tres puntos no colineales.
b. Dos puntos cualesquiera de un plano determinan una recta, que esta contenida en el plano.
POSTULADOS DEL ESPACIO
a. El espacio contiene al menos cuatro puntos que no son coplanarios.
b. Por un punto del espacio pasan infinitas rectas.
c. Por una recta del espacio pasan infinitos planos.
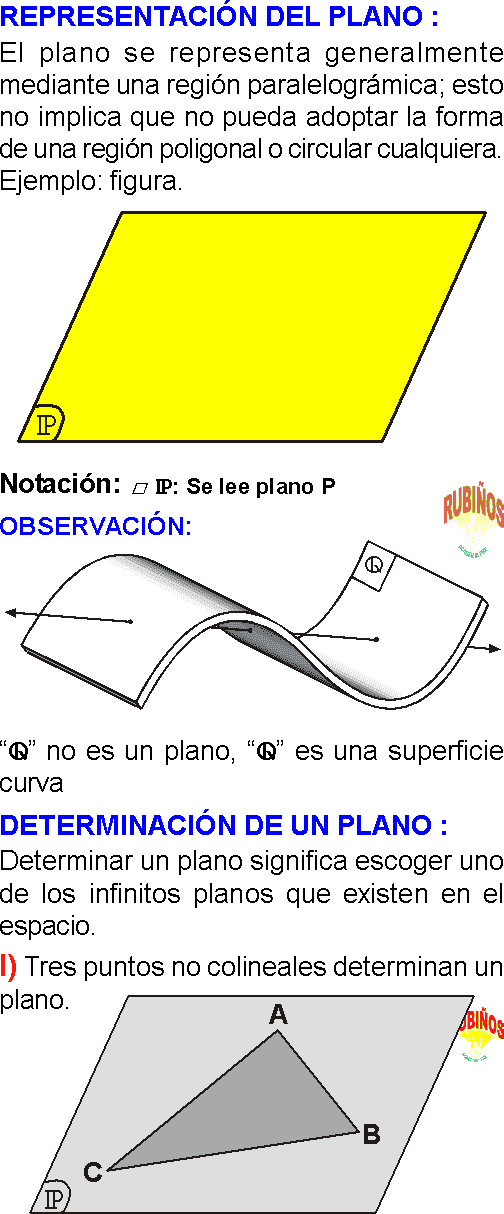
DETERMINACIÓN DE UN PLANO
Un plano queda determinado por:
a. Tres puntos no colineales.
b. Una recta y un punto exterior a ella.
c. Dos rectas secantes.
d. Dos rectas paralelas.
POSICIONES RELATIVAS DE DOS RECTAS EN EL ESPACIO
a. Rectas secantes
Cuando se intersectan y tiene por tanto un punto común.
Las rectas secantes son coplanares.
b. Rectas paralelas
Cuando se encuentran en un mismo plano y no se intersectan.
c. Rectas coincidentes
Cuando se superponen, para lo cual basta que tenga dos puntos comunes.
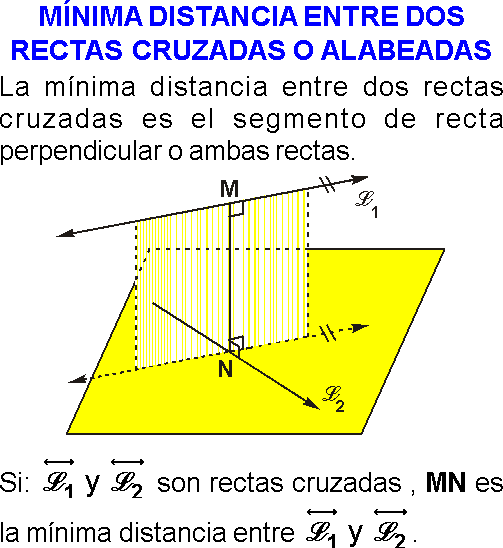
d. Rectas alabeadas.
Llamado también rectas que se cruzan, son aquellas rectas que no están en un mismo plano y no tiene ningún punto común.
*
*














































.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)

