RAZONES TRIGONOMÉTRICAS DE ÁNGULOS EN POSICIÓN NORMAL EJERCICIOS RESUELTOS PDF
✎ Ángulos en posición normal y sus R.T.
✎ Signo de las razones trigonométricas en los cuadrantes
✎ Ángulos cuadrantales
✎ Razones trigonométricas negativas
✎ Ángulos coterminales
APRENDIZAJES ESPERADOS
• Reconocer un ángulo en posición normal.
• Conocer las definiciones de las razones trigonométricas de un ángulo en posición normal.
• Calcular los valores de las razones trigonométricas de cualquier ángulo.
• Identificar el signo de las razones trigonométricas, según la posición del ángulo.
• Calcular y aplicar los valores de los ángulos cuadrantales.
Para que una estación espacial realice sus funciones, sus partes deben acoplarse de manera standar, porque sino su funcionamiento no sería óptimo.
En el caso de los ángulos trigonométricos, para calcular sus razones trigonométricas éstos deben hallarse también en una forma adecuada, es decir deben encontrarse en posición normal (standar).
Este tema es muy importante debido a que se puede determinar razones trigonométricas para todo tipo de ángulo, sea positivo o negativo y poner énfasis en hallar ángulos referenciales debido a que nos sirve para el siguiente tema que es reducción al primer cuadrante.
ÁNGULO EN POSICIÓN NORMAL , CANÓNICA O ESTANDAR
Es un ángulo trigonométrico que cumple las siguientes características :
𝑖) El vértice coincide con el origen de coordenadas.
𝑖𝑖) La posición inicial del rayo está en el eje positivo de las abscisas.
𝑖𝑖𝑖) La posición final del rayo posee cualquier ubicación en el plano cartesiano .
Un ángulo trigonométrico está en POSICIÓN NORMAL si su vértice esta en el origen de coordenadas y su lado inicial coincide con el lado positivo del eje X.
Si el lado final esta en el segundo cuadrante, el ángulo se denomina ÁNGULO DEL SEGUNDO CUADRANTE y análogamente para los otros cuadrantes.
Si el lado final coincide con un eje se dice que el ÁNGULO NO PERTENECE A NINGÚN CUADRANTE.
DEFINICIÓN DE LAS RAZONES TRIGONOMÉTRICAS PARA UN ÁNGULO EN POSICIÓN ESTÁNDAR
Si “θ” es un ángulo en cualquier posición normal y P(x;y) es un punto cualquiera que pertenece a su lado final, sus razones trigonométricas se calculan con el triángulo rectángulo formado al trazar desde “P” segmentos dirigidos a los ejes coordenados, por tanto el valor de los catetos serán las distancias dirigidas “x” e “y” y el valor de la hipotenusa será siempre un número positivo “r”.
Para mayor comprensión de la definición hacemos el siguiente cambio.
cateto opuesto = y = ordenada
cateto adyacente = x = abscisa
hipotenusa = r = radio vector
ÁNGULO CUADRANTAL
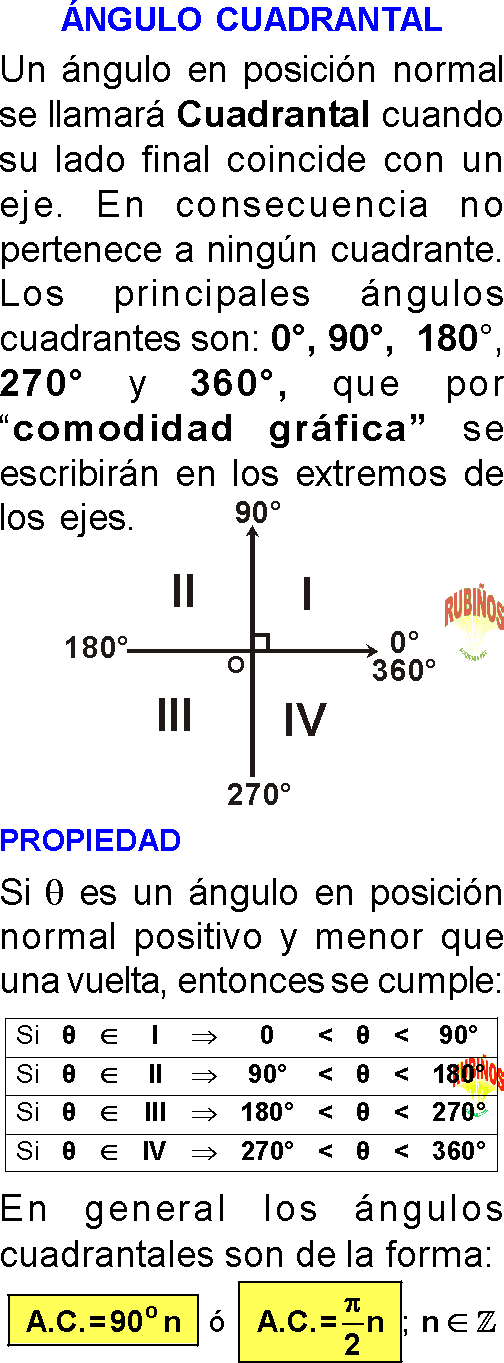
Un ángulo en posición normal se llamará CUADRANTAL cuando su lado final coincide con un eje. En consecuencia no pertenece a ningún cuadrante.
Los principales ángulos cuadrantes son: 0°, 90°, 180°, 270° y 360°, que por “comodidad gráfica” se escribirán en los extremos de los ejes.
SIGNOS DE LAS RAZONES TRIGONOMÉTRICAS EN CADA CUADRANTE
En los ejemplos anteriores algunas razones trigonométricas resultaron positivas y otras negativas. Esto dependerá del cuadrante en el que se ubique el ángulo considerado, en las figuras siguientes se aprecia un criterio para recordar los signos; entendiéndose que están indicadas las que son positivas y sobreentendiendo que las no mencionadas en cada cuadrante, son negativas.
PRIMER CUADRANTE :
En el primer cuadrante TODAS las R.T. son POSITIVAS, porque LA ABSCISA (x) , la ordenada (y), el radio vector (r) son positivos.
SEGUNDO CUADRANTE :
En el segundo cuadrante el SENO y la COSECANTE son positivas , porque la ordenada (y), el radio vector (r) son positivas. Las demás R.T. son negativas.
TERCER CUADRANTE :
En el tercer cuadrante la TANGENTE y COTANGENTE son positivas , porque la abscisa (x), la ordenada (y) son negativas. La demás R.T: son negativas.
CUARTO CUADRANTE :
En el cuarto cuadrante el COSENO y la SECANTE son positivas , porque la abscisa (x) y el radio vector (r) positivos. Las demás R.T. son negativas.
Es suficiente conocer el signo de dos razones trigonométricas diferentes que no sean reciprocas, para saber a que cuadrante pertenece el ángulo en Posición Normal
! RECUERDA ¡
Los ángulos cuadrantales son aquellos ángulos canónicos, cuyo lado final coincide con cualquiera de los semiejes cartesianos. Su medida es siempre múltiplo de 90° y no pertenecen a ningún cuadrante.
RAZONES TRIGONOMÉTRICAS DE ÁNGULOS CUADRANTALES
Como ejemplo modelo vamos a calcular la R.T. de 90°, análogamente se va a calcular las otras R.T. de 0°; 180° ; 270° y 360°
ÁNGULOS COTERMINALES
Dos ángulos en posición normal se llama COTERMINALES o COFINALES si tienen el mismo lado final y mismo lado inicial.
GUIA BÁSICA
EJERCICIO 1 :
Calcular el radio vector del punto (3; 4).
EJERCICIO 2 :
Calcular el radio vector de los puntos (2; 1) y (1; 3).
EJERCICIO 3 :
Calcular el radio vector del punto (–5; 12).
EJERCICIO 4 :
El punto (–5; –12) pasa por el lado final de un ángulo en posición normal.
Calcular el radio vector de dicho punto.
EJERCICIO 5 :
El punto (–24; –7) pasa por el lado final de un ángulo en posición normal.
Calcular coseno del ángulo en posición normal.
EJERCICIO 6 :
Calcular la tangente de un ángulo en posición normal, sabiendo que el punto (7; 9) pasa por el lado final de dicho ángulo.
EJERCICIO 7 :
El punto (2; 8) pertenece al lado final de un ángulo en posición normal.
Calcular la cotangente del ángulo.
EJERCICIO 8 :
El punto (–2; 3) pasa por el lado final de un ángulo en posición normal.
Calcular la tangente de dicho ángulo.
EJERCICIO 9 :
Si el lado final de un ángulo β en posición normal pasa por el punto (–12; –5).
Calcule secβ – cscβ
EJERCICIO 10 :
Si el lado final de un ángulo en posición normal pasa por el punto (–2, 1).
Calcular la cosecante de dicho ángulo.
EJERCICIO 11 :
Si el punto (–5;–12) pasa por el lado final de un ángulo en posición normal.
Calcular la secante de dicho ángulo.
EJERCICIO 11 :
Calcular sen90+cos90º
EJERCICIO 12 :
Calcular tg180º – sec180º
EJERCICIO 13 :
Calcular (cos90º+sen180º)cos360º
EJERCICIO 14 :
Calcular sen90º.sec360º.tg0º
EJERCICIO 15 :
Calcular cos0º – sec0º.cos360º
EJERCICIO 16 :
Calcular sec0º.csc90º.sec180º
EJERCICIO 17 :
Si el punto (3;–4) pasa por el lado final de un ángulo en posición normal. Calcular la cosecante del ángulo.
A) –5/4
B) 5/3
C) 5/4
D) –5/3
E) 3/5
EJERCICIO 18 :
Calcular la tangente de un ángulo en posición normal. Si el punto (–5; 4) pasa por el lado final del ángulo.
A) 4/5
B) –4/5
C) 3/5
D) 3/4
E) –3/4
PROBLEMAS PROPUESTOS
PREGUNTA 1 :
Si senθ= − 1/3 y tgθ < 0 , hallar el valor de √2(sec θ + tgθ).
A) –1
B) 0
C) 1
D) –2
E) 2
Rpta. : "C"
PREGUNTA 2 :
Si 81tg²θ – 1600=0 y el ángulo θ pertenece al cuarto cuadrante, calcule 9secθ – 41senθ
A) 85
B) 63
C) 72
D) 81
E) 78
Rpta. : "D"
PREGUNTA 3 :
Si α es un ángulo en posición normal, 6sen²α − 19senα + 10 = 0 y α∈II C ; hallar √5tgα + 2
A) 2
B) 0
C) 1
D) – 1
E) – 2
Rpta. : "B"
PREGUNTA 4 :
Indicar el ángulo que no es coterminal al ángulo – 10°.
A) 350°
B) 710°
C) 1420°
D) – 730°
E) 1070°
Rpta. : "C"
PREGUNTA 5 :
A es un ángulo del tercer cuadrante cuya tangente es 2,4 y B es un ángulo del segundo cuadrante para el cual es cierto que senB = cos A + sen(−A) .
Calcular 49[ctg²B + csc(– B)]
A) 29
B) 211
C) 38
D) 120
E) 91
Rpta. : "A"
PREGUNTA 6 :
Si α es un ángulo en posición normal para el cual tgα= – 3 y |cosα| = cosα
hallar √10(cos α − senα)
A) 4
B) 5
C) – 1
D) – 2
E) – 4
Rpta. : "A"
PREGUNTA 7 :
Los ángulos α y β son coterminales y para ellos es cierto que 0 < α < 2𝛑 y 6𝛑 < β < 8𝛑.
Si α + 2β = 2535°, calcular α + β.
A) 1330°
B) 1280°
C) 1380°
D) 1220°
E) 1480°
Rpta. : "A"
PREGUNTA 8 :
Si α y β son ángulos coterminales, α perteneciente al cuarto cuadrante y 12sen²α – 5senβ – 3=0 , halle tgα + secβ
A) 1/3
B) 3/2
C) 3/4
D) √2/2
E) √3/4
Rpta. : "D"
PREGUNTA 9 :
Si se cumple que 15sen²β – 14 senβ – 8=0 , donde β es un ángulo en posición normal del tercer cuadrante, calcule el valor de ctgβcoβ
A) –2,4
B) –2,5
C) –2,3
D) –2,1
E) –2,2
Rpta. : "D"
PREGUNTA 10 :
Los ángulos α y β son coterminales y (–2;a) con a<3 es un punto del lado terminal de β . Si ctgα+tgβ=– 13/6 , calcule 6csc²α – ctgβ .
A) 4/7
B) 12/7
C) 4/25
D) 19/4
E) 3/2
Rpta. : "B"
PREGUNTA 11 :
Si |cosα| = – cosα , |ctgα| = ctgα y |senα| = 3/4 , calcule √7(2tgα – secα)
A) 2
B) 10
C) 7
D) 12
E) 8
Rpta. : "B"
PREGUNTA 12 :
Dos ángulos coterminales están en la relación de 5 a 4. Si el mayor ángulo está comprendido entre 3900° y 6800°, calcule la suma de las medidas de dichos ángulos.
A) 9720°
B) 6480°
C) 7620°
D) 12960°
E) 10800°
Rpta. : "A"
PREGUNTA 13 :
Si β es un ángulo en posición normal que satisface la ecuación 5cos²β + √5cosβ – 2=0 y además ctgβ>0 , senβ<0 , calcule el valor de la expresión (cscβ + 2secβ)² .
A) 16
B) 18
C) 19
D) 20
E) 21
Rpta. : "D"
PREGUNTA 14 :
Determine, respectivamente, el signo de las siguientes expresiones:
I. sen²θ – tanθ; θ ∈IVC
II. sen²α +cscα; α ∈IIC
III. cotβ – senβ; β ∈IIIC
A) +, +, –
B) +, –, +
C) –, –, +
D) +, +, +
Rpta. : "D"
PREGUNTA 15 :
Si senθ√(senθcosθ)<0, ¿a qué cuadrante pertenece θ?
A) IIC
B) IIIC
C) IVC
D) IC o IIIC
Rpta. : "B"
PREGUNTA 16 :
Si secθ= 25/24 y senθ<0, calcule tanθ
A) 7/24
B) 24/7
C) − 3/4
D) − 7/24
Rpta. : "D"
PREGUNTA 17 :
¿Cuántos ángulos cuadrantales existen entre 0º y 630º?
A) 4
B) 5
C) 7
D) 6
Rpta. : "D"
PREGUNTA 18 :
Si α y θ son ángulos cuadrantales positivos menores que una vuelta, tal que √tanα = sen³θ−1, calcule α – θ
A) 180º
B) 0
C) 90º
D) –180º
Rpta. : "C"
PREGUNTA 19 :
Se sabe que α y θ son ángulos cuadrantales positivos y menores que una vuelta, dichos ángulos cumplen las siguientes condiciones:
senα+3=sec60°
cosθ = sen270°+ cos360°
α ≠θ
calcule α +θ
A) 270°
B) 180°
C) 450°
D) 360°
Rpta. : "C"
PREGUNTA 20 :
Sea β un ángulo en posición normal que pertenece al II cuadrante, tal que 6cos²β – cosβ= 1. Halle el valor de √2cotβ
A) −1/3
B) − 1/2
C) –1
D) –2
E) −3/4
Rpta. : "B"
PREGUNTA 21 :
Si tanψ> 0 y cosψ<0, determine el signo de las siguientes expresiones:
E=senψsecψ
D= cotψ – cscψ
U=cos³ψ +senψ
A) +; –; +
B) +; +; –
C) +; +; +
D) –; +; –
E) –; –; +
Rpta. : "B"
PREGUNTA 22 :
Si f(x) =sen³x – cos³x calcule el valor de f(90°) + f(180°)
A) –2
B) –1
C) 0
D) 1
E) 2
Rpta. : "E"
PREGUNTA 23 :
Si θ∈IIIC y β∈IIC, además tan²θ + cot²β +13= 2(2tanθ – 3cotβ), calcule √5secθ+ √10cscβ
A) 3
B) 5
C) 7
D) 0
E) 12
Rpta. : "B"
PREGUNTA 24 :
¿ 𝐶𝑢á𝑛𝑡𝑜𝑠 á𝑛𝑔𝑢𝑙𝑜𝑠 𝑐𝑢𝑎𝑑𝑟𝑎𝑛𝑡𝑎𝑙𝑒𝑠; ℎ𝑎𝑦 𝑒𝑛𝑡𝑟𝑒 100° 𝑦 890°.
𝐴) 5
𝐵) 6
𝐶) 7
𝐷) 8
Rpta. : "D"
PREGUNTA 25 :
𝑆𝑖 𝛽 𝑒𝑠 𝑢𝑛 á𝑛𝑔𝑢𝑙𝑜 𝑐𝑢𝑎𝑑𝑟𝑎𝑛𝑡𝑎𝑙 𝑝𝑜𝑠𝑖𝑡𝑖𝑣𝑜 𝑦 𝑚𝑒𝑛𝑜𝑟 𝑞𝑢𝑒 𝑢𝑛𝑎 𝑣𝑢𝑒𝑙𝑡𝑎 𝑡𝑎𝑙 𝑞𝑢𝑒 ∶
𝑡𝑎𝑛𝛽 = 𝑐𝑜𝑠180° + 𝑐𝑠𝑐90°; 𝑐𝑎𝑙𝑐𝑢𝑙𝑒 𝑒𝑙 𝑣𝑎𝑙𝑜𝑟 𝑑𝑒 𝛽 + 10°
𝐴) 100°
𝐵) 10°
𝐶) 190°
𝐷) 370°
Rpta. : "C"
PROBLEMAS RESUELTOS
PREGUNTA 1 :
Si : Secα = −2,666... ; Senα > 0 ; hallar el valor de la siguiente expresión:
F = Ctgα − Cscα
A) √55/5
B) − √55/5
C) 5
D) −√55
E) √55
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 2 :
Calcular:
2(a – b)sen𝛑/2 +3(a – b)cos𝛑 – (b – a)csc𝛑2
A) a–b
B) 2(a+b)
C) 4(a–b)
D) 0
RESOLUCIÓN :
R.T. de un ángulo de cualquier magnitud
=2(a – b)(1) +3(a – b)(–1) – (b – a)(1)
=2a – 2b – 3a+3b – b+a
=0
Rpta. : "D"
PREGUNTA 3 :
En la figura mostrada ABC es una semicircunferencia, en donde MN⊥OB y O es el origen de coordenadas.
Calcule el valor de cot(α) + cot(β).
A) 1/3
B) 3/2
C) 3/4
D) −2/3
E) 2/3
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 4 :
Si
entonces el valor de E=ctgθ – cosθ es:
A) – √15/4
B) – 3√15/4
C) – 5√15/4
D) – 3√15/2
E) – 5√15/2
RESOLUCIÓN :
Rpta. : "C"
