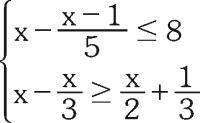ÁLGEBRA SIMULACRO BECA 18 PRUEBA PRONABEC SOLUCIONARIO
PREGUNTA 1 :
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 2 :
Halle el residuo de la siguiente división:
A) 6x+5
B) 6x – 5
C) 5x – 6
D) 2x – 3
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 3 :
Sea
f(x)=a(x – h)2 + k
cuya gráfica se da a continuación:
Hallar el valor de “a”.
A) 2
B) – 2
C) – 3
D) 3
RESOLUCIÓN :
Funciones
Del gráfico; el vértice de la parábola es (1;2), entonces:
f(x)=a(x – 1)2 + 2
Luego, (0 ;– 1) ∈ f , entonces:
– 1=a(0 – 1)2 + 2⇒ a= – 3
Rpta. : "C"
PREGUNTA 4 :
Luego de resolver el siguiente sistema:
Halle el número de valores enteros del conjunto solución
A) 6
B) 7
C) 8
D) 9
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 5 :
Reducir la siguiente expresión:
Luego de como respuesta los dos tercios de E.
A) 19/13
B) 3/2
C) 13/19
D) 2/3
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 6 :
Halle la ecuación de la recta cuya gráfica se da a continuación.
A) 2x+3y – 2=0
B) 2x+3y – 6=0
C) 2x-3y – 6=0
D) 6x+2y – 3=0
RESOLUCIÓN :
Funciones
Sea la ecuación: y=mx+b , donde b=2.
Entonces, y=mx+2, luego reemplazando el punto (3;0) en la función, se tiene que x= – 2/3
Luego y= – 2/3x + 2
Que despejando es equivalente a 2x+3y – 6=0
Rpta. : "B"
PREGUNTA 7 :
Dada la siguiente gráfica de la función “F”
¿Cuántas de las siguientes proposiciones son verdaderas?
I. El rango de f es [ – 3;3[
II. La pendiente de f es – 3 en el intervalo ]0;3[
III. f(8) – f( – 8)=0
A) Solo I
B) Solo II
C) Solo III
D) Ninguna
RESOLUCIÓN :
Funciones
I. (F), el rango es [ – 3;3]
II. (F), la recta está inclinada hacia la derecha en el intervalo ]0;3[ debe ser positiva
III. (F), f(8)=3 f( – 8)= – 3
⇒ f(8) – f( – 8)=6
Rpta. : "D"
PREGUNTA 8 :
Halle el rango de la función F: ℝ →ℝ, cuya regla de correspondencia es:
F(x)= – x2+4x
A) ] – ∞;+4]
B) [4; ∞[
C) ] – 4;+∞[
D) ] – ∞; – 4]
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 9 :
Calcular la suma de valores de ''x'' en la ecuación:
A) 5
B) 6
C) 7
D) 8
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 10 :
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 11 :
Determina el valor de “x” en la ecuación
logx+log2x=log(9x+5)
A) 1/2
B) 5
C) 1
D) 4
RESOLUCIÓN :
Ecuaciones logarítmicas
Restricción por definición: x>0
Luego, por teorema:
logx+log2x=log(x.2x)
Reemplazando:
log(2x2)=log(9x+5)
2x2=9x+5
Debido a la restricción: x=5
Rpta. : "B"
