MAGNITUDES PROPORCIONALES EJERCICIOS RESUELTOS PDF
OBJETIVOS DE APRENDIZAJE :
☛ Reconocer las magnitudes directamente proporcionales.
☛ Recocer las magnitudes inversamente proporcionales.
☛ Aplicar las propiedades de magnitudes en la resolución de problemas.
☛ Resolver problemas asociados a sistemas de engranajes.
SUBTEMAS
☛ Nociones previas: definición de magnitud , definición de cantidad.
☛ Relaciones entre magnitudes: directamente proporcional (DP) , inversamente proporcional (IP)
☛ Interpretación gráfica en cada caso función de proporcionalidad directas inversa.
☛ Propiedad de magnitudes
APLICACIONES COTIDIANAS
☛ Elaborar una receta de cocina es una actividad de magnitudes directamente proporcionales
☛ Calcular el precio de una excursión es una actividad de magnitudes inversamente proporcionales.
MAGNITUD
Se define magnitud matemática a toda característica de un objeto que se pueda medir o contar.
CANTIDAD
Es un valor particular que toma una magnitud en un determinado momento del análisis.
MAGNITUDES DIRECTAMENTE PROPORCIONALES
Dos magnitudes son directamente proporcionales (DP) , cuando al aumentar o disminuir el valor de una de ellas, el valor de la otra magnitud también aumenta o disminuye respectivamente en la misma proporción.
MAGNITUDES INVERSAMENTE PROPORCIONALES
Dos magnitudes son inversamente proporcionales (IP) , cuando al aumentar o disminuir el valor de una de ellas, el valor de la otra magnitud disminuye o aumenta respectivamente en la misma proporción.
PRIMERA PRACTICA
EJERCICIO 1 :
A es directamente proporcional con B² e inversamente proporcional a √C , cuando:
A = 4; B = 8; C = 16. Hallar "A", cuando: B = 12; C = 36.
a) 8
b) 6
c) 10
d) 4
e) 12
EJERCICIO 2 :
"x" varía en forma directa a "y" e inversa al cuadrado de "z". Cuando x=10, entonces: y=4; z=14. Hallar "x", cuando: y=16; z=7.
a) 160
b) 180
c) 140
d) 150
e) 200
EJERCICIO 3 :
"A" varía proporcionalmente a "B" y al cuadrado de "C" e inversamente proporcional a "D". Si cuando: A = 8; B = 5 y C = 4, entonces "D" es 2. ¿Cuánto valdrá "B" cuando: A = 2D ; D = 4C?
a) 160
b) 180
c) 100
d) 140
e) 120
EJERCICIO 4 :
"A" es directamente proporcional con "B" e inversamente proporcional con "C", cuando "C" es igual a 3/2, "A" y "B" son iguales. ¿Cuál es el valor de "B" cuando "A" es igual a 1 y "C" es igual a 12?
a) 6
b) 11
c) 10
d) 8
e) 9
EJERCICIO 5 :
"A" varía directamente con la raíz cuadrada de "B" e inversamente con el cubo de "C". Si: A = 3; B = 256; C = 2, hallar "B", cuando: A = 24 ; C = 1/2.
a) 8
b) 4
c) 9
d) 16
e) 6
EJERCICIO 6 :
Si "A" es directamente proporcional a "B" y "C" e inversamente proporcional con "D" y "E". Cuando: A = 2B; D = 4; C = 2, entonces: E = 2. Calcular "E" cuando: A = 72; D = 6; B = 2 ; C = 3E².
a) 9
b) 8
c) 7
d) 10
e) 15
EJERCICIO 7 :
¿Cuál es el peso de un diamante que vale S/. 5 500, si uno de cinco gramos cuesta S/. 22 000 y el precio es proporcional al cuadrado de su peso?
a) 2,5 g
b) 2
c) 2,4
d) 3,5
e) 3,8
EJERCICIO 8 :
El precio de un pasaje varía inversamente con el número de pasajeros. Si para 14 pasajeros, el pasaje es S/.15, ¿cuántos pasajeros serán cuando el pasaje cueste S/. 6?
a) 31
b) 33
c) 34
d) 36
e) 35
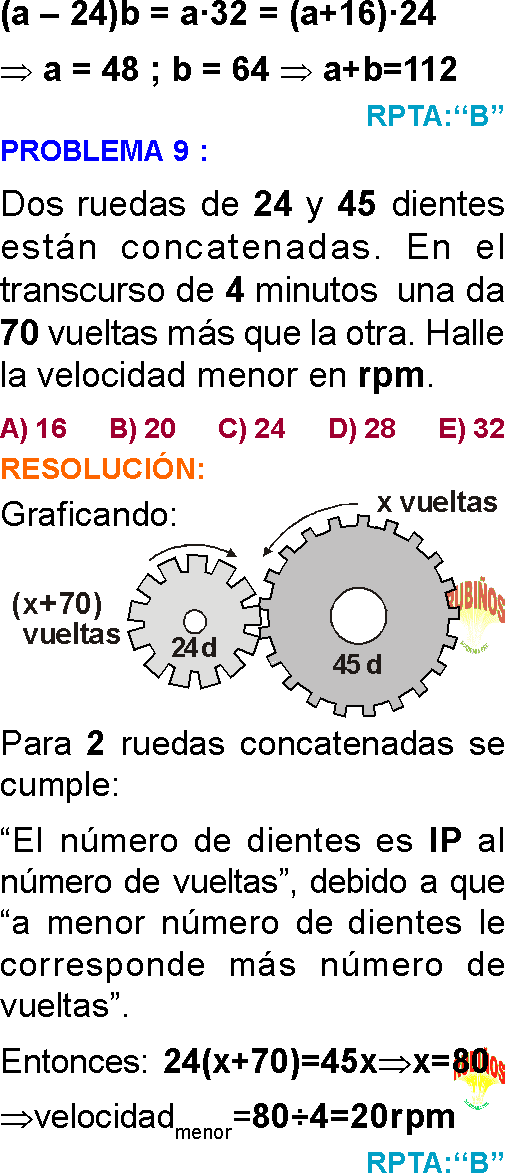
EJERCICIO 9 :
En una empresa el sueldo de un empleado es proporcional al cuadrado del número de años de servicio. Si un empleado tiene actualmente 15 años de servicio, ¿dentro de cuántos años cuadruplicará su sueldo?
a) 15
b) 30
c) 8
d) 45
e) 60
EJERCICIO 10 :
El peso de un elefante es D.P. a sus años, si un elefante tuviera 360 kg tendría 32 años. ¿Cuál es su edad si pesa 324 kg?
a) 28 años y 248 días
b) 28 años y 294 días
c) 27 años y 294 días
d) 28 años y 292 días
e) 28 años y 228 días
EJERCICIO 11 :
El precio de un diamante es directamente proporcional al cuadrado de su peso. Si un diamante que pesa 20 gramos cuesta 4 000 dólares, ¿cuánto costará otro diamante que pesa 25 gramos?
a) $ 6 000
b) 5 000
c) 7 500
d) 4 800
e) 6 250
EJERCICIO 12 :
El precio de un diamante es proporcional al cuadrado de su peso. Si un diamante de cuatro quilates vale S/. 1 280, ¿cuál es el peso de un diamante que vale S/. 3 920?
a) 5 quilates
b) 14
c) 3
d) 7
e) 6
EJERCICIO 13 :
Una rueda "A" de 80 dientes se encuentra concatenada con otra rueda "B" de 45 dientes. Si la rueda "A" gira 36 vueltas en un minuto, ¿cuántas vueltas dará "B" en el mismo tiempo?
a) 80
b) 64
c) 100
d) 120
e) 150
EJERCICIO 14 :
Una rueda "A" de 80 dientes, engrana con otra rueda "B" de 30 dientes. Si la rueda "A" da 12 vueltas por minuto, ¿cuántas vueltas dará la rueda "B" en cinco minutos?
a) 160
b) 120
c) 100
d) 200
e) 250
EJERCICIO 15 :
Sabiendo que "A" es I.P. a B⁴ y "C" es D.P. a "B". Hallar "A", cuando: C=8; si: A=96 y C=4.
a) 2
b) 3
c) 4
d) 9
e) 6
EJERCICIO 16 :
El precio de un diamante es directamente proporcional al cuadrado de su peso. Si un diamante cuesta $ 500, ¿cuánto costará otro diamante que pesa el doble del anterior?
a) $ 1 000
b) 1 500
c) 2 000
d) 2 500
e) 3 000
EJERCICIO 17 :
El precio de un diamante es D.P. al cuadrado de su peso. ¿Cuánto se perdería si un diamante de $ 32 000 se rompe en dos pedazos siendo uno el triple del otro?
a) $ 5 000
b) 10 000
c) 12 000
d) 6 000
e) 15 000
EJERCICIO 18 :
Si "A" varía directamente proporcional a "B" e inversamente proporcional con "C²". A su vez "C" varía directamente proporcional con "E". Cuando: B=20 ; E=4, entonces: A=80. Hallar "A", cuando: B=120 ; E=8.
a) 100
b) 120
c) 140
d) 150
e) 160
EJERCICIO 19 :
El precio de un diamante es D.P. al cuadrado de su peso. Si un diamante que pesa 80 gramos cuesta $3 200, ¿cuánto costará otro diamante de 100 gramos de peso?
a) $ 4 000
b) 4 500
c) 5 000
d) 8 000
e) 10 000
EJERCICIO 20 :
La corriente de un tubo electrónico es D.P. al cubo de la raíz cuadrada del voltaje. Si el voltaje se hace tres veces mayor, ¿cuántas veces mayor se hace la corriente?
a) 3
b) 4
c) 5
d) 8
e) 7
EJERCICIO 21 :
La aceleración que adquiere un cuerpo es directamente proporcional a la fuerza que se le aplica. Si una fuerza de 80 N produce una aceleración de 5 m/s², ¿qué aceleración producirá una fuerza de 48 N?
a) 2 m/s²
b) 3
c) 4
d) 5
e) 6
SEGUNDA PRACTICA
PREGUNTA 1 :
El precio de un diamante es DP al cuadrado de su peso. Si un diamante se parte en 2 pedazos, uno de los cuales pesa los dos quintos del otro, y se venden ambos pedazos, sufriendo una pérdida de 20 000 dólares, determine el precio inicial del diamante antes de romperse.
A) $49 000
B) $52 000
C) $40 000
D) $38 000
Rpta. : "A"
PREGUNTA 2 :
Sean M y N dos magnitudes, tal que M DP √N . Si se sabe que el valor de M es 16 cuando el valor de N es 108, calcule el valor de N cuando el valor de M sea 8.
A) 27
B) 18
C) 30
D) 15
Rpta. : "A"
PREGUNTA 3 :
El Olivar es un albergue para conejos de todas las razas y tiene víveres (pienso, heno, otros) para 62 días, pero llegan cuatro conejitos más, por ello los víveres solo alcanzan para 60 días. Determine cuántos conejitos había inicialmente en el albergue.
A) 80
B) 120
C) 112
D) 108
Rpta. : "B"
PREGUNTA 4 :
Se tienen 2 magnitudes A y B que son IP, cuando A aumenta en 25%, B varía en 6 unidades. Calcule el valor inicial de B.
A) 24
B) 25
C) 18
D) 30
Rpta. : "D"
PREGUNTA 5 :
Una piscina se llena en 6 h con un grifo que arroja 120 L de agua por minuto. ¿Cuánto tiempo tardará en llenar la piscina otro grifo que arroja 80 L por minuto?
A) 9 h
B) 10 h
C) 12 h
D) 14 h
Rpta. : "A"
PREGUNTA 6 :
Si A y B son magnitudes que tienen cierta relación de proporcionalidad.
A 8 x 50 18 12
B 6 21 15 y 24
Halle: x+ y
A) 98
B) 100
C) 107
D) 113
Rpta. : "C"
PREGUNTA 7 :
El precio de un terreno cuadrado es DP al área e IP a la distancia de Lima; si un terreno ubicado a 150 km de Lima cuesta $20 000. ¿Cuánto costará otro terreno cuyo perímetro es la mitad del anterior y se encuentra a 100 km de Lima?
A) $6000
B) $6500
C) $7000
D) $7500
Rpta. : "D"
PREGUNTA 8 :
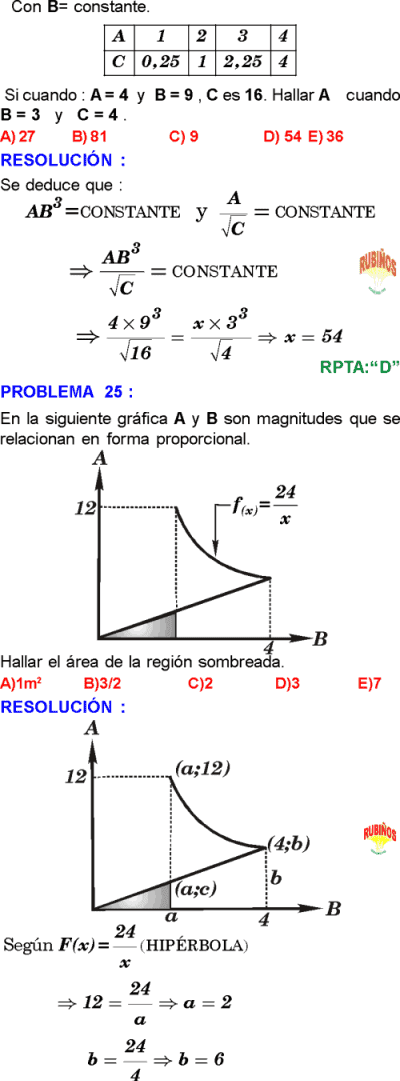
Dadas las magnitudes A, B y C tal que: A dp B2 (C: constante) y √C IP A (B: constante) Si cuando A= 15; B= 5 y C= 16. Halle el valor de “A” cuando B= 10 y C= 25.
A) 24
B) 36
C) 48
D) 54
Rpta. : "C"
PREGUNTA 9 :
El sueldo de un empleado es proporcional a su eficiencia e inversamente proporcional al número de días que ha faltado a trabajar. Luis tuvo un sueldo mensual de S/2400 y su eficiencia es como 5 y faltó 4 días a trabajar. Determine cuál es el sueldo de Marco si el rendimiento de este es como 8 y faltó 3 días a trabajar.
A) S/3600
B) S/4800
C) S/5120
D) S/5020
Rpta. : "C"
PREGUNTA 10 :
El calor producido por una plancha es DP al cuadrado de la corriente eléctrica y al tiempo transcurrido; si una plancha produce 2000 calorías cuando circula una corriente de 2 amperios durante 10 minutos. Halle la corriente que circula por la misma plancha durante 5 minutos para producir 4000 calorías.
A) 8 A
B) 9 A
C) 10 A
D) 12 A
Rpta. : "A"
PREGUNTA 11 :
Se sabe que A es DP a B e IP a 3C; además cuando A= 14 entonces B= 64 y C=B. Halle el valor de “A” cuando B= 4 y C=2B.
A) 3
B) 5
C) 7
D) 9
Rpta. : "C"
PREGUNTA 12 :
Dadas las magnitudes A, B y C tal que: A DP √B (C: constante) y C² IP A (B: constante) si cuando A= 3; B= 36 y C= 8. Halle el valor de “B” cuando A= 6 y C= 4.
A) 9
B) 16
C) 25
D) 36
Rpta. : "A"
PREGUNTA 13 :
El costo de un libro es proporcional al número de páginas que tiene e IP al número de libros editados. Un libro valorizado en S/80 se va a reeditar duplicando ahora la cantidad de libros y al agregarle gráficos incrementará en su mitad el número de páginas. ¿Cuál será el nuevo costo?
A) S/30
B) S/35
C) S/40
D) S/45
Rpta. : "A"
PREGUNTA 14 :
Se tiene tres ruedas engranadas A, B y C de 72; 54 y 90 dientes, respectivamente. Si la rueda B da 120 RPM, determine la diferencia del número de vueltas que dan las ruedas A y C en 3 min.
A) 30
B) 54
C) 48
D) 72
Rpta. : "B"
PREGUNTA 15 :
Una rueda A de 40 dientes engrana con otra rueda B de 50 dientes, fijo al eje de B hay otra rueda C de 24 dientes. Si C da 72 vueltas en 5 min, determine cuántas vueltas dará A en 2 min.
A) 27
B) 90
C) 50
D) 36
Rpta. : "D"
PREGUNTA 16 :
La fuerza de sustentación sobre el ala de un avión es DP a su área y al cuadrado de la velocidad; si se aumenta el área en un 20 % y se reduce la velocidad en un 10%. ¿Qué sucede con la fuerza de sustentación?
A) Aumenta en 3,7%
B) Disminuye en 4,2%
C) Disminuye en 2,8%
D) Aumenta en 1,6%
Rpta. : "C"
PREGUNTA 17 :
Se tienen tres ruedas (A, B y C) dispuestas de modo que A engrana con B y esta a su vez engrana con C. Se sabe que A y B tienen 30 y 50 dientes, respectivamente, y que A y C dan 80 y 120 RPM, respectivamente. Calcule cuántas vueltas por minuto da B.
A) 72
B) 48
C) 36
D) 21
Rpta. : "B"
PREGUNTA 18 :
En un sistema de engranajes, la rueda A de 40 dientes engrana con B de 60 dientes, la cual está unida mediante un eje a la rueda C de 50 dientes, que a su vez engrana con D de 40 dientes. Si en t minutos las cuatro ruedas dieron 570 vueltas, halle el número de vueltas de C en 2t minutos.
A) 102 vueltas
B) 96 vueltas
C) 192 vueltas
D) 120 vueltas
Rpta. : "D"
PREGUNTA 19 :
Si con 2 máquinas del tipo A o con 5 máquinas del tipo B se puede realizar un trabajo en 6 h, ¿en cuántas horas se realizará el mismo trabajo si funcionan juntas 2 máquinas del tipo A y una del tipo B?
A) 8 h
B) 4 h
C) 5 h
D) 3 h
Rpta. : "C"
PREGUNTA 20 :
Un reservorio de 8 metros de radio y 12 metros de altura abastece a 75 personas durante 20 días. ¿Cuál debe ser el radio de un reservorio de 6 metros de altura que debe abastecer a 50 personas durante 2 meses?
A) 14 m
B) 16 m
C) 18 m
D) 20 m
Rpta. : "B"
PREGUNTA 21 :
La velocidad de un automóvil es DP a la potencia de un motor e IP al cuadrado del número de personas que viajan en él; si un automóvil que tiene una potencia de 20 HP y lleva 2 personas desarrolla una velocidad de 60 km/h. ¿Qué potencia tendrá otro automóvil que lleva 4 personas a una velocidad de 45 km/h?
A) 30 HP
B) 40 HP
C) 50 GB
D) 60 HP
Rpta. : "D"
PREGUNTA 22 :
El precio de una casa es DP al área e IP a la distancia de Lima; si una casa ubicada a 75 km de Lima cuesta $45 000. ¿Cuánto costará una casa del mismo material si su área es el triple de la anterior y se encuentra a 150 km de Lima?
A) $59 500
B) $67 500
C) $70 500
D) $78 500
Rpta. : "B"
PROBLEMAS RESUELTOS
PREGUNTA 1 :
Sea R la tasa de infección viral, V el número de virus en una célula, C el número de células y t el tiempo en horas, donde RCt=V
La relación que define la tasa de infección es
A) células por horas/virus.
B) virus por células/horas.
C) virus por horas/células.
D) virus/células por horas.
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 2 :
En un circo, se sabe que los radios de la llanta trasera y delantera de una bicicleta están en la relación de 4 a 5 respectivamente. Cuando el malabarista se desplace en dicha bicicleta y la llanta delantera dé 36 vueltas, ¿cuántas vueltas habrá dado la llanta trasera de la bicicleta?
A) 36
B) 45
C) 40
D) 42,5
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 3 :
Con los valores de las magnitudes: obreros y tiempo, se realizó el siguiente gráfico: Determina (x+y).
A) 55
B) 35
C) 65
D) 40
E) 82
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 4 :
El gráfico muestra el comportamiento de dos magnitudes inversamente proporcionales. Halle el valor de y/x
A) 5
B) 50
C) 100
D) 20
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 5 :
En una financiera, un equipo de 16 analistas de créditos trabajando al 60% de su capacidad en 12 días a razón de 6 horas diarias pueden atender a 200 clientes. ¿Cuántos analistas trabajando al 90% de su capacidad en 8 días a razón de 10 horas diarias pueden atender a 250 clientes?
A) 9
B) 7
C) 11
D) 8
E) 12
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 6 :
Elena realizó algunas pruebas experimentales con un nuevo modelo de auto y los datos obtenidos se muestran en la gráfica:
Calcule la velocidad a los (b+4a+3)÷a segundos.
A) 14 m/s
B) 42 m/s
C) 35 m/s
D) 28 m/s
E) 49 m/s
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 7 :
Se tiene el siguiente sistema, determine el número de vueltas que da la rueda M, si la rueda N da 20 vueltas.
A) 35
B) 32
C) 36
D) 34
E) 33
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 8 :
Tres socios aportan 1000, 1500 y 2000 soles respectivamente para la formación de una empresa. Al cabo de cierto tiempo, obtienen un beneficio de 4500 soles.
¿Cuánto ganó el que aportó menor capital?
a) 1000 soles
b) 1250 soles
c) 900 soles
d) 1200 soles
e) 500 soles
RESOLUCIÓN :
.png)
Rpta. : "A"
PROPORCIONALIDAD COMPUESTA
En la vida diaria podemos apreciar que los valores que representan a una magnitud dependen generalmente de un conjunto de magnitudes, las cuales pueden ser clasificadas como D.P. o I.P.
La proporcionalidad compuesta nos permite describir las fórmulas matemáticas que se usan en otros campos de la ciencia como la física y la química.
Debemos recordar que cuando las magnitudes son inversamente proporcionales, los productos de los valores que la representan nos dan una constante.
Si dos magnitudes son directamente proporcionales , el cociente de los valores que respectivamente las representan es constante.
