LONGITUD DE ARCO Y SECTOR CIRCULAR PROBLEMAS RESUELTOS PDF

En la actualidad, se utilizan con frecuencia arcos de circunferencia debido a su estética y a su capacidad de contener volumen máximo. 

Existen variedades de diseños de estructuras arquitectónicas, como, por ejemplo, las cúpulas, portales, tanques de almacenamiento, carreteras. 

Entiéndase por áreas circulares al área de un círculo, de un sector circular y de un trapecio circular. 

La distancia constante desde el centro a cualquier punto de la circunferencia se le denomina radio. 

ARCO DE CIRCUNFERENCIA 

Es aquella porción de circunferencia limitada por dos puntos de la misma. 

ÁREA DEL SECTOR CIRCULAR 

Es aquella porción del círculo 

Se denomina sector circular a la región geométrica que limita dos radios de una misma circunferencia y el arco limitado por dichos radios. 

La región limitada por dos arcos de circunferencia que tienen el mismo centro y los segmentos cuya longitud es la diferencia de sus radios se denomina trapecio circular. 

ÁREA DE UN TRAPECIO CIRCULAR 

Dado un trapecio circular, se puede obtener su área a partir de la diferencia del área del sector mayor menos el área del sector menor, sin embargo, también es posible utilizar otra expresión para el área

ÁREA DE LA CORONA CIRCULAR

Es aquella región obtenida por la diferencia de las áreas de dos círculos 

OBJETIVOS : 

• Aplicar correctamente la fórmula para el cálculo de la longitud de un arco de circunferencia.

• Calcular  el valor del área de un sector circular. 

• Identificar y explicar los conceptos vertidos en situaciones cotidianas. 

PREGUNTAS PROPUESTAS

PROBLEMA 1 :

Halla la longitud de una circunferencia si el ángulo central de 1rad subtiende un arco de longitud 6m. 

a) 12𝛑m 

b) 13𝛑m 

c) 14𝛑m 

d) 16𝛑m 

e) 19𝛑m 

Rpta. : "A"

PROBLEMA 2 :

Halla la longitud de un arco en un sector circular cuyo ángulo central mide 60° y el radio 12m. 

a) 2𝛑m 

b) 4𝛑m 

c) 6𝛑m 

d) 8𝛑m 

e) 12𝛑m 

Rpta. : "B"

PROBLEMA 3 :

Determina la longitud de arco de un sector cuyo ángulo central mide (x/3) rad y su radio mide (6x)m; sabiendo además que el perímetro de este sector es de 110m. 

a) 20m 

b) 30m 

c) 40m 

d) 50m 

e) 60m 

Rpta. : "D"

PROBLEMA 4 :

Halla la longitud del arco de un sector circular de ángulo central 45°, sabiendo que la longitud de la circunferencia es 600m. 

a) 75m 

b) 60m 

c) 120m 

d) 65m 

e) 80m 

Rpta. : "A"

PROBLEMA 5 :

Si a un sector circular, se le triplica el radio y a su ángulo central se le disminuye en 36°; se obtendrá un nuevo sector de longitud de arco igual al doble de la longitud del arco inicial; determina la longitud del nuevo ángulo central. 

a) 𝛑/10 rad 

b) 𝛑/5 rad 

c) 2𝛑/5 rad 

d) 3𝛑/5 rad 

e) 3𝛑/10 rad 

Rpta. : "C"

PROBLEMA 6 :

Si a un sector circular se le duplica el ángulo central y a su radio se le disminuye en 3m, se obtendrá un nuevo sector de longitud de arco igual a la mitad de la longitud del arco inicial; determina el radio del nuevo sector. 

a) 5m 

b) 4m 

c) 3m 

d) 2m 

e) 1m 

Rpta. : "E"

PROBLEMA 7 :

Si a un sector circular se le duplica el ángulo central y a su radio se le reduce en 3m, se obtendrá un nuevo sector cuya área es la mitad que la del área del sector inicial, determina el radio del sector inicial. 

a) 2m 

b) 3m 

c) 4m 

d) 5m 

e) 6m 

Rpta. : "E"

PROBLEMA 8 :

Si a un sector circular le cuadruplicamos su ángulo central y aumentamos 5m a su radio, se obtendrá que el sector resultante tiene un área que es 49 veces el área del sector inicial; determina el radio del sector resultante. 

a) 1m 

b) 3m 

c) 5m 

d) 7m 

e) 9m 

Rpta. : "D"

PROBLEMA 9 :

Un sector circular tiene un ángulo central de 9º y su radio mide 36 m. Si se quiere aumentar su ángulo en 7º , ¿en cuánto habrá que disminuir su radio para que su área no varíe? 

A) 7 m 

B) 8 m 

C) 9 m 

D) 10 m 

E) 11 m 

Rpta. : "C"

PROBLEMA 10 :

Si el ángulo central de un sector circular se reduce a la mitad, su longitud de arco del sector circular se disminuye en 5𝛑 u. Calcule la longitud de arco del sector. 

A) 10𝛑 u 

B) 4𝛑 u 

C) 5𝛑 u 

D) 8𝛑 u 

E) 9𝛑 u 

Rpta. : "A"

PROBLEMA 11 :

El Sr. Rojas desea cercar con alambre un terreno que tiene forma de sector circular, tal que su ángulo central y radio miden 117° y 40 m respectivamente. En base a la información dada, ¿cuántos metros de alambre necesitará el Sr. Rojas para cercar dicho terreno? 

A) (40+36𝛑) m 

B) (80+26𝛑) m 

C) (70+26𝛑) m 

D) (80 – 26𝛑) m 

E) (80+16𝛑) m 

Rpta. : "B"

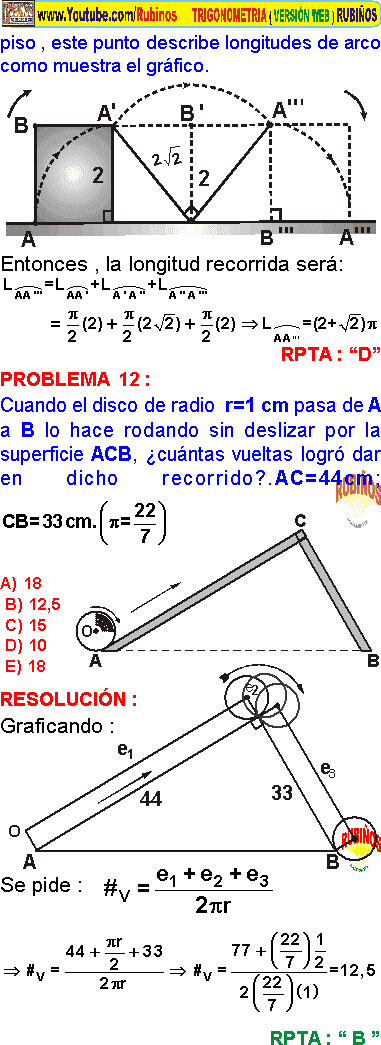
PROBLEMA 12 :

El profesor de Física le pide a sus alumnos que determinen la rapidez de un móvil, el cual se desplaza con movimiento uniforme sobre un arco de circunferencia de 200 m de diámetro. Si el mejor alumno de la clase observa que en 20 s , el móvil recorre un arco cuyo ángulo central es 50g , determine la rapidez de dicho móvil. 

A) 3𝛑 m/s 

B) 5𝛑/4 m/s 

C) 7 m/s 

D) 9𝛑/4 m/s 

E) 5𝛑/3 m/s 

Rpta. : "B"

PROBLEMA 13 :

Se tiene una lámina de aluminio en forma de sector circular cuyo ángulo central es (20000/3)m. Si se desea cubrir el arco con una cinta de 6𝛑/7 m , este no queda cubierto totalmente; pero si es cubierto con una cinta de 10𝛑/7 m , sobra una longitud dos veces más de lo que faltaba anteriormente. Teniendo en cuenta la información dada, determine el radio de dicha lámina. 

A) 3 m 

B) 5 m 

C) 4 m 

D) 7 m 

E) 6 m 

Rpta. : "A"

PROBLEMA 14 :

En uno de los ejercicios de trigonometría, Miguel observa que si se duplican las medidas del ángulo central y del radio de un sector circular se obtiene un nuevo sector de área Mu² . Si el área del sector inicial es 2 N u² , determine M÷N . 

A) 4 

B) 16 

C) 8 

D) 12 

E) 10 

Rpta. : "C"

PROBLEMA 15 :

El Sr. Sifuentes traslada todos los días a su hija Cecilia a su centro de estudios una distancia aproximada de 1,5 km a lo largo de una pista horizontal y plana. Si el diámetro de una de las llantas es de 0,6 m y N representa el número de vueltas que da dicha llanta, calcule el valor de N𝛑/5 

A) 1/10

B) 10 

C) 7 

D) 5 

E) 1/5 

Rpta. : "D"