DIVISIBILIDAD EJERCICIOS RESUELTOS PDF
APRENDIZAJES ESPERADOS
☛ Conocer los conceptos de múltiplo y divisor.
☛ Reconocer los números no divisibles respecto a un módulo.
☛ Conocer los principios de divisibilidad.
☛ Estudiar el principio de Arquímedes y su aplicación en la resolución de problemas.
☛ Conocer los principales criterios de divisibilidad.
☛ Aplicar los criterios de divisibilidad en la resolución de problemas.
La teoría de divisibilidad surge entre otras situaciones, por la necesidad de explicar la división de dos cantidades enteras, cuando esta no resulta ser exacta, es decir por ejemplo de encontrar el residuo que se obtiene sin necesitad de efectuar la operación de división.
En nuestra rutina diaria hay una gran cantidad de ocasiones en las que usamos los múltiplos y divisores de un número sin darnos cuenta, con la finalidad de resolver dichas situaciones en forma práctica y precisa.
¿Qué es divisibilidad?
Es la parte de la matemática que estudia las condiciones que debe reunir un número para que se pueda dividir en forma exacta por otro.
DEFINICIÓN
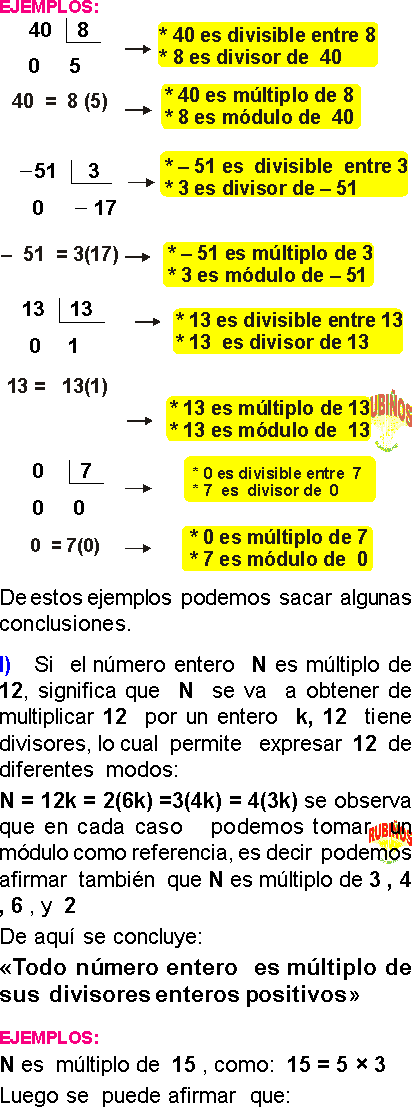
Un número entero “A” es divisible entre otro entero positivo “B”, si la división de “A” entre “B” es exacta, es decir el cociente es entero y el residuo es igual a cero.
OBSERVACIONES
I) El cero es múltiplo de todo número entero positivo.
II) Todo número entero positivo es múltiplo de si mismo.
III) La unidad es divisor de todo número entero .
IV) Si el número entero N es múltiplo de 12, significa que N se va a obtener de multiplicar 12 por un número k , 12 tiene divisores, lo cual permite expresar de diferentes modos:
N=12k=2(6k)=6(2k)=3(4k)=4(3k) ; se observa que en cada caso podemos tomar un módulo como referencia , es decir podemos afirmar también que N es múltiplo de 3 ó 4 ó 2 de aquí se concluye:
“ Todo número entero es múltiplo de sus divisores enteros positivos ”
Hasta este momento nos hemos dedicado principalmente a la representación de los múltiplos de un módulo, veamos ahora como podríamos representar los múltiplos de un módulo.
Sabemos, que si un número entero es no múltiplo (divisible) de otro entero positivo, al efectuar la división respectiva sería inexacta, es decir que el residuo sería diferente de cero. Pero la división inexacta se puede realizar de 2 formas: por defecto o por exceso.
PRACTICA PROPUESTA
PREGUNTA 1 :
Del 1 al 300. ¿Cuántos son múltiplos de 17 ?
A) 17
B) 13
C) 21
D) 16
E) 15
Rpta. : "A"
PREGUNTA 2 :
Del 1 al 100, ¿Cuántos son múltiplos de 7?
A) 13
B) 14
C) 12
D) 17
E) 27
Rpta. : "B"
PREGUNTA 3 :
Del 1 al 200, ¿Cuántos son múltiplos son de 37?
A) 4
B) 5
C) 6
D) 7
E) 8
Rpta. : "A"
PREGUNTA 4 :
Del 1 al 100. ¿Cuántos son múltiplos de 6?
A) 16
B) 19
C) 14
D) 28
E) 35
Rpta. : "A"
PREGUNTA 5 :
Del 630 al 2840, ¿Cuántos múltiplos de 6?
A) 328
B) 308
C) 358
D) 369
E) 378
Rpta. : "D"
PREGUNTA 6 :
¿Cuántos múltiplos de 9 hay entre 13 hasta 234?
A) 23
B) 24
C) 25
D) 27
E) 26
Rpta. : "C"
PREGUNTA 7 :
El número de invitados a una fiesta es tal que si se agrupan de 30 en 30 sobran 9 ; si se agrupan de 18 en 18 sobran 9 y si se agrupan de 24 en 24 también sobran 9. ¿Cuál es el número de invitados , si se sabe que no son más de 400?
A) 200
B) 220
C) 400
D) 420
E) 369
Rpta. : "E"
PREGUNTA 8 :
Del 1 al 42. ¿Cuántos números no son múltiplos de 2 ni de 3?
A) 12
B) 13
C) 14
D) 7
E) 21
Rpta. : "C"
PREGUNTA 9 :
¿Cuál es el menor número mayor que 800, que al ser dividido entre 25, deja 20 de residuo y al ser dividido entre 40 deja 30 de residuo?
A) 830
B) 840
C) 850
D) 860
E) 870
Rpta. : "E"
PREGUNTA 10 :
¿Cuántos números divisibles entre 4 y 5 , existe entre 301 y 499?
A) 9
B) 8
C) 7
D) 6
E) 10
Rpta. : "A"
PREGUNTA 11 :
¿Cuál es el mayor número natural menor que 1000, que al ser dividido por 18; 32 y 24 dé un residuo común que sea el mayor posible?
A) 724
B) 737
C) 837
D) 881
E) 908
Rpta. : "D"
PREGUNTA 12 :
Determine si las siguientes proposiciones son verdaderas (V) o falsas (F) y elija la secuencia correcta.
I. El 1 es divisor de todo número entero.
II. El 4 y 6 son divisores de 84.
III. El 40 es múltiplo de 80.
A) FVV
B) VVV
C) VFV
D) VVF
E) FFF
Rpta. : "D"
PREGUNTA 13 :
Los alumnos del curso de física se sientan en bancas de 7 alumnos, excepto la última banca donde se sientan 8 alumnos, cuando van al laboratorio se sientan en mesas de 4 alumnos , salvo un alumno que se sienta solo. ¿Cuál es el número de alumnos si se sabe que está comprendido entre 76 y 92. Dar como respuesta la suma del número hallado?
A) 12
B) 15
C) 13
D) 10
E) 11
Rpta. : "C"
PREGUNTA 14 :
¿Cuántos números comprendidos entre 104 y 926 son divisibles entre 17?
A) 50
B) 49
C) 47
D) 48
E) 56
Rpta. : "D"
PREGUNTA 15 :
Un carpintero compra un número de tornillos que es mayor que 700 pero que 800. si los cuenta de 15 en 15 sobran 10; si los cuenta de 20 en 20 sobran 15 y si los cuenta de 24 en 24 sobran 19.¿Cuántos tornillos compró?
A) 705
B) 715
C) 825
D) 785
E) 935
Rpta. : "B"
PREGUNTA 16 :
¿Cuántos números de tres cifras son múltiplos de 6, pero no de 5?
A) 120
B) 150
C) 90
D) 75
E) 140
Rpta. : "A"
PREGUNTA 17 :
Un empleado trabaja 5 días seguidos y descansa el sexto. Empieza su trabajo el lunes. ¿Cuántos días tienen que transcurrir para que le toque descansar un domingo?
A) 30 Días
B) 33
C) 41
D) 42
Rpta. : "C"
PREGUNTA 18 :
Calcule la suma de los números que son múltiplos de 8 y que están comprendidos entre 50 y 200.
A) 2180
B) 2232
C) 2432
D) 2360
E) 1820
Rpta. : "B"
PREGUNTA 19 :
Un una fábrica un empleado trabaja 4 días seguidos y descansa el 5to día. Si el empieza su trabajo un día lunes, ¿Cuántos días tienen que transcurrir para que le toque descansar un Domingo?
A) 35
B) 34
C) 36
D) 40
E) 38
Rpta. : "B"
PREGUNTA 20 :
La edad que tiene Érika es más de 30 años, pero menor que 40, y es múltiplo de 4; además dentro de 8 años su edad será múltiplo de 11. Halle la suma de cifras de la edad de Érika.
A) 9
B) 10
C) 11
D) 12
E) 15
Rpta. : "A"
PREGUNTA 21 :
El número de alumnos que se encuentran en un aula es menor que 240 y mayor que 100 , se observa que los 2/7 del total usan anteojos y los 5/13 son alumnos de la especialidad de ciencias. ¿Cuál es la suma de los alumnos que usan anteojos con los alumnos de la especialidad de ciencias?
A) 130
B) 125
C) 122
D) 150
E) 160
Rpta. : "C"
PREGUNTA 22 :
Lewis tiene 2030 lapiceros que los va a repartir equitativamente a un grupo de personas, de tal manera que siempre sobran 20. ¿De cuántas maneras se puede hacer esa distribución?
A) 6
B) 7
C) 8
D) 9
E) 5
Rpta. : "D"
PREGUNTA 23 :
De las proposiciones:
I) 2853 es divisible por 9
II) 2488 es divisible por 8
III) 3360 es divisible por 5; 6 y 7
Son verdaderas
A) Sólo I
B) Sólo II
C) Sólo I y II
D) II y III
E) I; II y III
Rpta. : "E"
PREGUNTA 24 :
En una biblioteca , se observó que la cantidad de estudiantes es menor que 300. Se sabe que los 3/4 del número total de estudiantes son de Varones, 1/6 son menores de 17 años y 7/10 se preparan por primera vez. ¿Cuál es la máxima cantidad de estudiantes que puede estar en dicha biblioteca?
A) 280
B) 250
C) 299
D) 240
E) 140
Rpta. : "D"
PREGUNTA 25 :
Se tiene un número de 3 cifras múltiplos de 9, si se invierte el orden de sus cifras el número es múltiplo de 5. el número total de decenas es múltiplo de 8. ¿Cuál es el producto de las cifras?
A) 120
B) 210
C) 200
D) 180
E) 20
Rpta. : "B"
PREGUNTA 26 :
Halle un número de 3 cifras que sea igual a 5 veces el producto de sus cifras. De como respuesta el producto de sus cifras.
A) 30
B) 35
C) 40
D) 45
E) 55
Rpta. : "B"
PREGUNTA 27 :
Una academia de fútbol tiene más de 100, pero menos de 200 pelotas. Si estas fueran contadas de 7 en 7, le sobrarían 5; pero si fueran contadas de 9 en 9, le sobrarían 7. Halle cuántas pelotas hay en total si al contarlas de 11 en 11 no sobra ninguna.
A) 187
B) 176
C) 165
D) 154
E) 140
Rpta. : "A"
PREGUNTA 28 :
Si en la academia los alumnos se colocan en filas de a 2; 3; 4; 5; ó 6 siempre sobra 1 pero si se colocan en fila de a 7, no sobra ninguno. ¿Cuántos alumnos hay si es menor que 400? Dar por respuesta la suma de sus cifras.
A) 7
B) 6
C) 9
D) 4
E) 3
Rpta. : "D"
PREGUNTA 29 :
A un viaje espacial fueron 141 personas, en ello se sabe que la novena parte de las mujeres se casaron con algunos marcianos y 17ava parte de los varones se convirtieron en reyes intergalácticos. ¿Cuántas mujeres no se casaron con los marcianos?
A) 20
B) 50
C) 60
D) 80
E) 15
Rpta. : "D"
PREGUNTA 30 :
Cuantos números comprendidos entre 2000 y 3000 terminan en la cifra 8 y son múltiplos de 17?
A) 5
B) 6
C) 10
D) 14
E) 12
Rpta. : "B"
PREGUNTA 31 :
En una fábrica en la que trabajan 150 empleados, salen de vacaciones cierto número de ellos. Si se agrupan los que quedan de a 10; de a 12; de a 15 y de a 20, sobran siempre 6 empleados; agrupándolos de a 18, no sobra ninguno. ¿Cuántos empleados hay de vacaciones? Dar por respuesta la suma de las cifras del resultado.
A) 8
B) 10
C) 9
D) 7
E) 11
Rpta. : "C"
PREGUNTA 32 :
Si usted tuviera las cifras 2 y 7 que otra cifra elegiría para escribir todos los números de tres cifras sin repetir ninguna cifra en su escritura sabiendo que la suma de dichos números es múltiplos de 13.
A) 2
B) 5
C) 8
D) 4
E) 7
Rpta. : "A"
PREGUNTA 33 :
Cual es el menor número de tres cifras que la suma de sus cifras es igual a 27 veces la suma de sus cifras.
A) 486
B) 504
C) 756
D) 135
E) 243
Rpta. : "E"
PREGUNTA 34 :
A un número de cuatro cifras consecutivas crecientes se le suma 988 y resulta un múltiplo de 44. Hallar la suma de las cifras del número.
A) 14
B) 18
C) 22
D) 26
E) 30
Rpta. : "B"
PREGUNTA 35 :
Carl Friedrich gauss llamado “El príncipe de las matemáticas” nació en Alemania en el siglo en un año tal que dividido entre 9 y 11 los residuos son 4 y 6 respectivamente. ¿Qué residuo deja al dividir dicho año entre 7?
A) 1
B) 2
C) 3
D) 4
E) 6
Rpta. : "E"