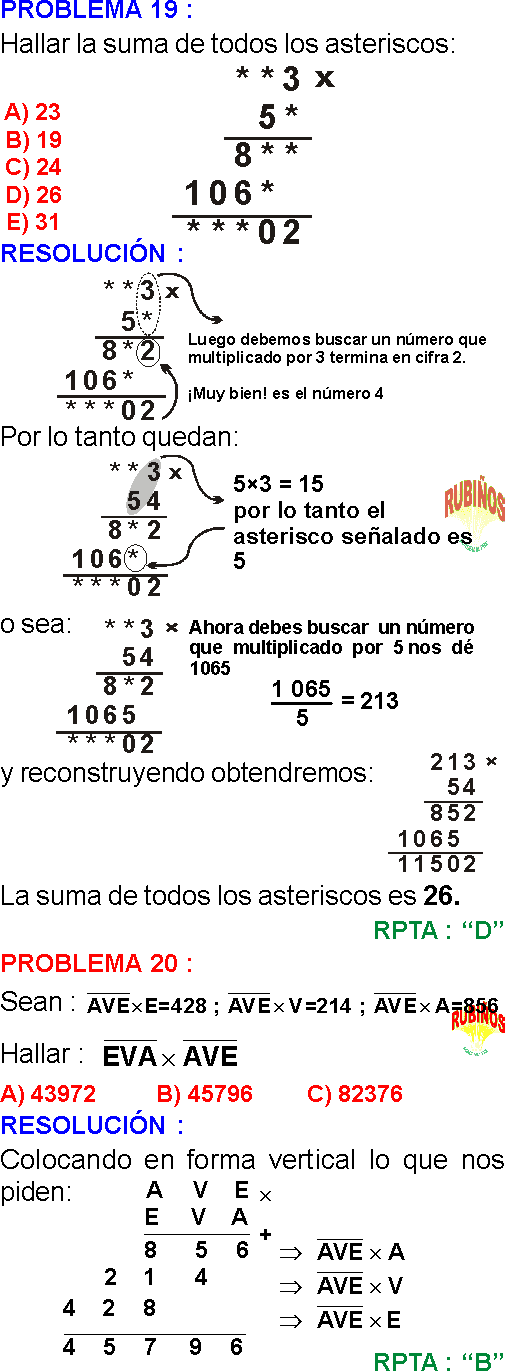
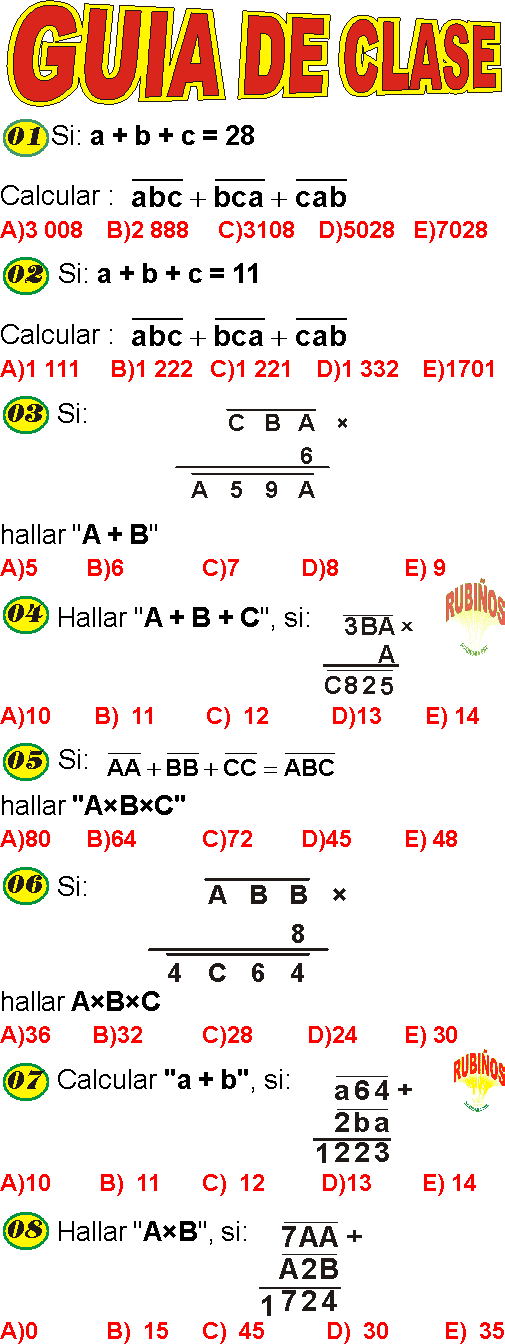
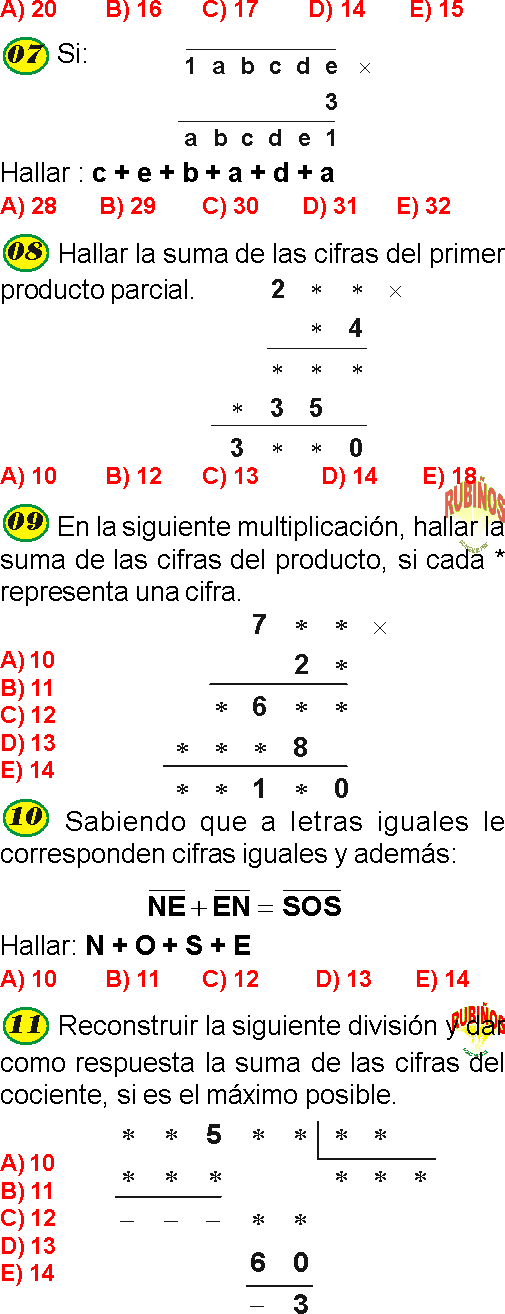
RAZONAMIENTO DEDUCTIVO EJEMPLOS Y PROBLEMAS RESUELTOS DE CRIPTO ARITMÉTICA–HABILIDAD LÓGICO MATEMÁTICA
RECONSTRUCCIÓN DE OPERACIONES MATEMÁTICAS BÁSICAS
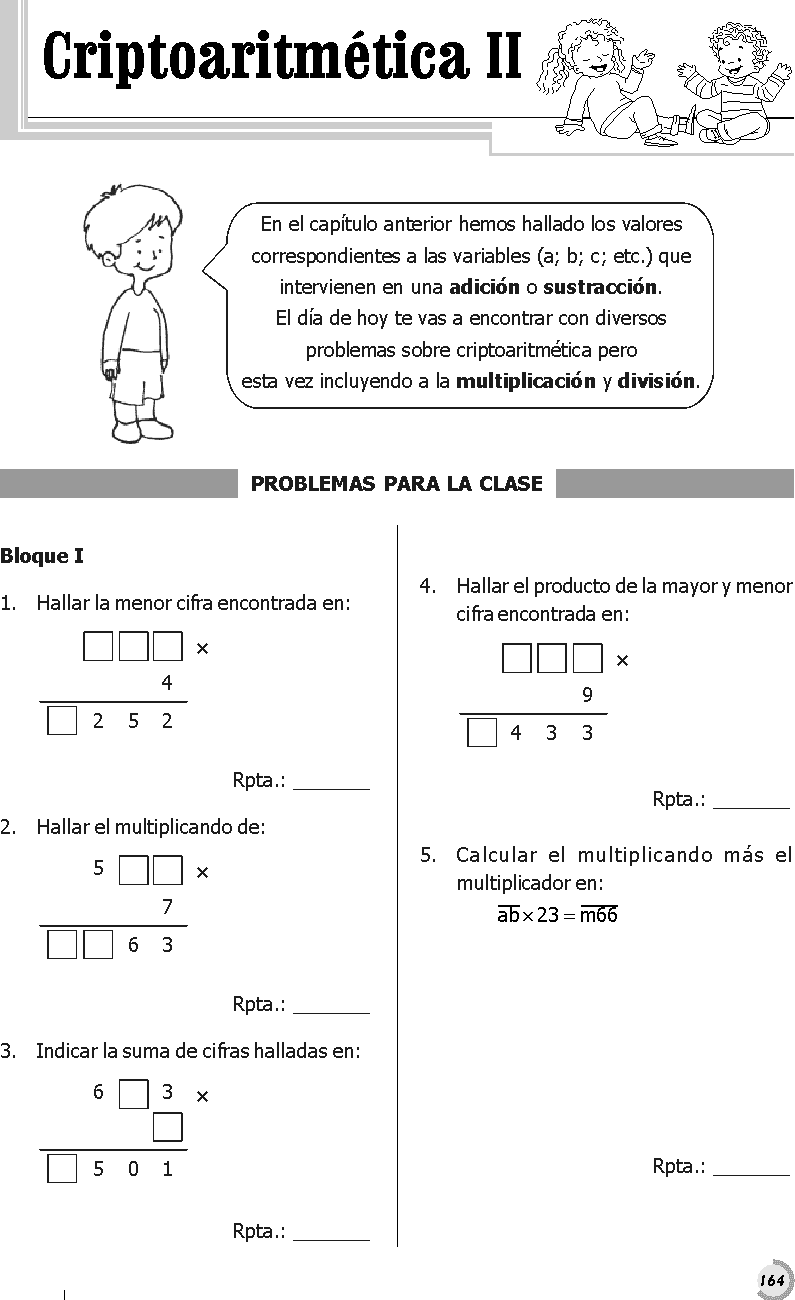
Cripto significa oculto, y hace referencia a las operaciones matemáticas, donde las cifras (todas o algunas) se han “ocultado” por medio de una letra , un asterisco o cualquier símbolo.
Este tema permite revalorar las operaciones básicas como adición , sustracción , multiplicación y división.
La idea de la cripto aritmética es rearmar las operaciones básicas de adición, sustracción, multiplicación, división, radicación y potenciación.
En los ejercicios que se abordan en este acápite, se cumple que :
─ a letras iguales le corresponde cifras iguales y a letras diferentes, cifras diferentes.
─ Cada letra, cada asterisco (*), representa una cifra.
─ La suma de dos dígitos como máximo es 18, siempre y cuando los dígitos sean iguales (9 + 9) y 17 si es que los dígitos son diferentes (9 + 8).
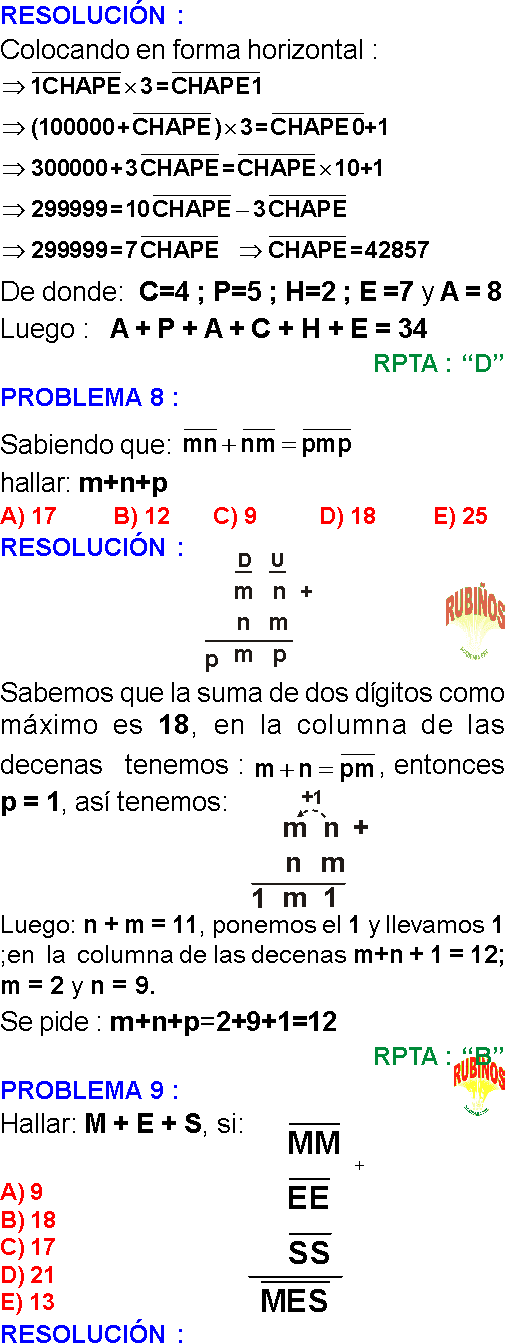
PREGUNTA 1 :
Hallar el valor de U + N + C
Si:
A) 11
B) 12
C) 13
D) 14
E) 15
RESOLUCIÓN :
PREGUNTA 2 :
Sea N un número natural tal que se cumple
12× N=...836
8×N=...224
Calcule las tres últimas cifras del resultado de multiplicar 28 ×N.
A) 144
B) 368
C) 284
D) 424
Rpta. : "C"
PREGUNTA 3 :
Se tiene un número de 3 cifras que comienza en 5 y acaba en 2; dichas cifras son cambiadas por 1 y 8, respectivamente. ¿En cuánto ha disminuido dicho número?
A) 388
B) 432
C) 406
D) 280
E) 394
PREGUNTA 4 :
Al multiplicar un número de 7 cifras consecutivas por 13, el resultado termina en 7. ¿Cuál será la diferencia entre la suma de cifras del resultado, con la suma de cifras del número de 7 cifras?
A) 0
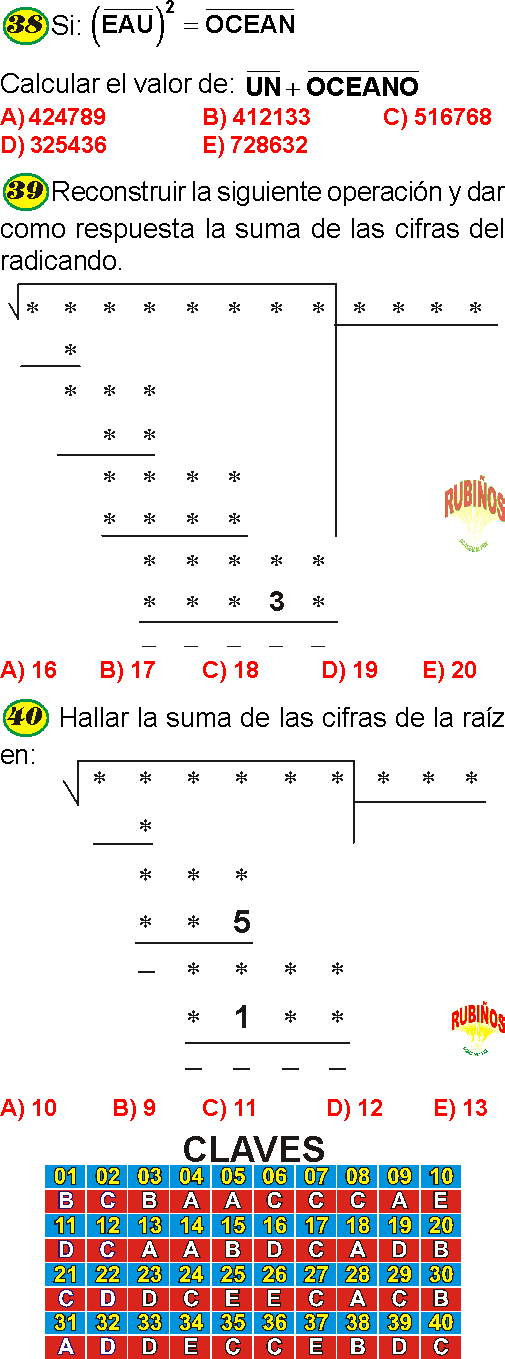
B) 1
C) 35
D) 14
E) 13
PREGUNTA 5 :
¿Cuál es el menor número que multiplicado por 24 nos da un producto cuyas cifras son todas 8?
A) 23
B) 888
C) 37
D) 45
E) 12
PREGUNTA 6 :
Las letras A, B, C y D representan a 4 números enteros tales que al dividirlos entre 5, dejan siempre residuos diferentes de cero y diferentes entre sí. ¿En qué cifra termina A +B+C+D?
A) en 5
B) en una cifra diferente de 0 y 5
C) en 0
D) en 5 o en 0
E) No se puede determinar.
PREGUNTA 7 :
Poseo cinco dígitos, pero si se me restara la unidad, ya no tendría cinco, sino solamente cuatro, ¿quien soy? (Dé como respuesta la suma de cifras del número).
A) 1
D) 2
B) 27
C) 36
E) 3
El origen del método deductivo se atribuye a los antiguos griegos, con el filósofo del silogismo, Aristóteles, y posteriormente desarrollado por Descartes, Spinoza y Leibniz.
En este tipo de razonamiento lógico es posible inferir las características a partir de una generalización.
Las generalizaciones siempre se ven afectadas por el proceso inductivo; mientras que las particularidades, por el deductivo.
El razonamiento deductivo presenta las conclusiones que necesariamente deben ser ciertas si todas las premisas son verdaderas.
Su base es racionalista y asume que solo la razón puede conducir al verdadero conocimiento. Por lo tanto, la idea detrás del método deductivo consiste en tener un principio reconocido como cierto e incuestionable, es decir, una premisa mayor a partir de la que el investigador establece relaciones con una proposición particular, la premisa menor. Ambas son comparadas para llegar a la verdad de lo que se propone, o conclusión.
Es importante aclarar que la deducción no ofrece nuevos conocimientos, ya que siempre conduce a la particularidad de una ley general anteriormente conocida.
El método deductivo solo organiza y especifica los conocimientos que ya se posee, desde un punto inteligible, es decir, la verdad general, ya se estableció, ir a otro punto interior de este plan deductivo parte de una hipótesis general. La fuente de la verdad para el deductivista es la lógica, mientras que para el inductivista es la experiencia.