SIGNIFICADO DE FRACCIÓN EJEMPLOS
Una fracción se interpreta como una forma de representar una parte de un todo.
Consiste en dos números separados por una línea horizontal, donde el número superior se llama numerador y el número inferior se llama denominador.
El numerador representa cuántas partes se toman del todo, mientras que el denominador indica en cuántas partes se divide el todo en total.
Por ejemplo, consideremos la fracción 5/8.
En esta fracción, el numerador es 5, lo que significa que estamos tomando 5 partes de un todo.
El denominador es 8, lo que indica que el todo se ha dividido en 8 partes iguales.
Por lo tanto, la fracción 5/8 representa tres de esas cuatro partes.
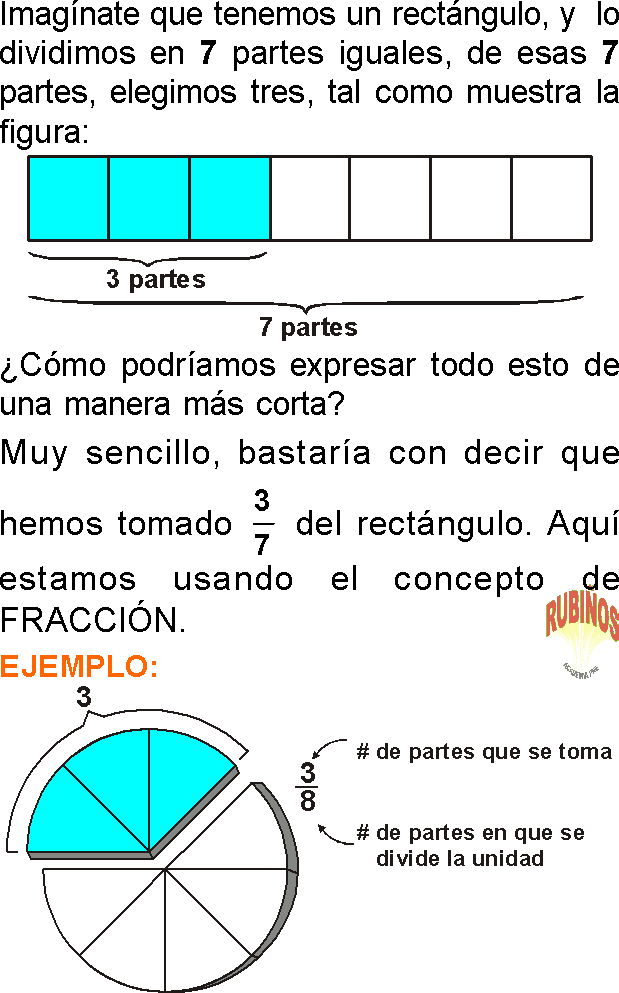
Otro ejemplo es la fracción 3/7. Aquí, el numerador es 3, lo que significa que estamos tomando 3 partes de un todo.
El denominador es 7, lo que indica que el todo se ha dividido en 7 partes iguales.
Así que la fracción 3/7 representa cinco de esas ocho partes.
En resumen, las fracciones nos permiten expresar partes de un todo de una manera precisa y relativa a la totalidad del objeto o cantidad en cuestión.