DERIVADAS TRIGONOMÉTRICAS EJERCICIOS RESUELTOS PDF
DERIVADA DE LA FUNCIÓN TRIGONOMÉTRICA SENO COSENO TANGENTE COTANGENTE SECANTE COSECANTE
OBJETIVOS
Al finalizar la unidad, el alumno será capaz de :
☛ Definir y conocer las derivadas de las funciones trigonométricas directas e inversas
☛ Derivar la función seno
☛ Derivar la función Coseno
☛ Derivar la función Tangente
☛ Derivar la función Cotangente
☛ Derivar la función Secante
☛ Derivar la función Cosecante
☛ Derivar el seno inverso o arco seno
☛ Derivar el coseno inverso o arco coseno
☛ Derivar la tangente inversa o arco tangente
☛ Derivar la cotangente inversa o arco cotangente
☛ Derivar la secante inversa o arco secante
☛ Derivar la cosecante inversa o arco cosecante
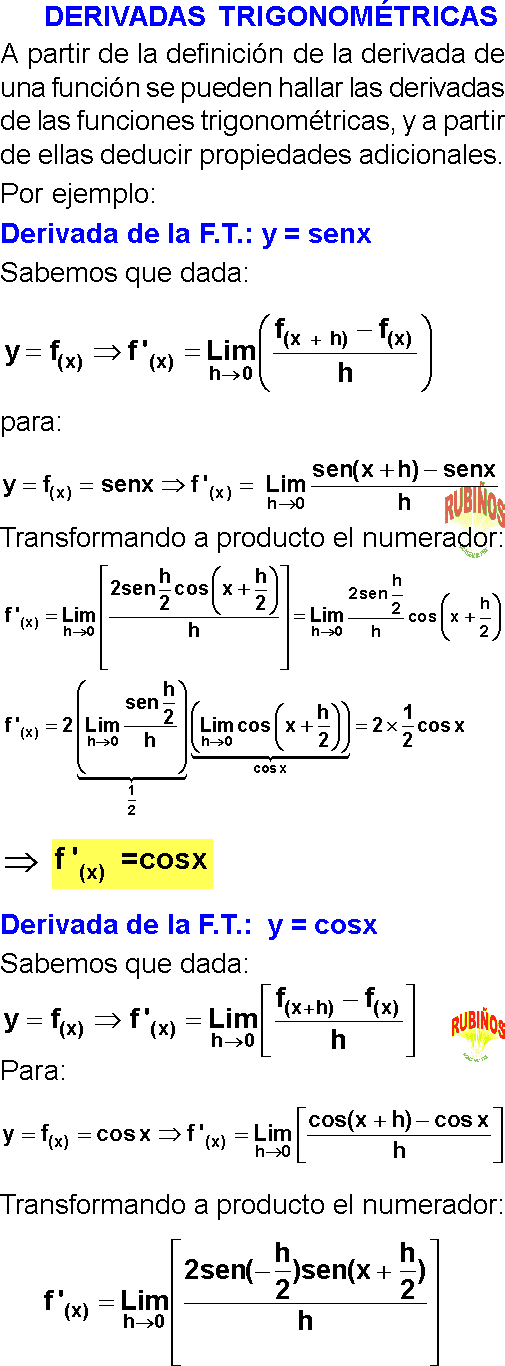
A partir de la definición de la derivada de una función se pueden hallar las derivadas de las funciones trigonométricas, y a partir de ellas deducir propiedades adicionales.
Conviene recordar que:
☛ Si una función es continua y estrictamente creciente (o decreciente) en un intervalo, entonces posee función inversa la cual también es continua y estrictamente creciente (o decreciente).
☛ Las funciones trigonométricas son periódicas por lo que la correspondencia entre la variable independiente y la dependiente no es uno a uno.
De aquí se tiene que la inversa de una función trigonométrica no es una función, es una relación.
Sin embargo, si se restringe el dominio de una función trigonométrica se establece una relación biunívoca y la inversa de la función trigonométrica sí es una función.
Una vez que se conocen las derivadas del senx y cosx, se puede calcular fácilmente las derivadas de las otras funciones trigonométricas circulares, ya que todas se pueden expresar en términos de seno o coseno.
Encontrar las derivadas de las funciones trigonométricas inversas implica el uso de la diferenciación implícita.
Derivada de la F.T.: y = senx
Derivada de la F.T.: y = cosx
Derivada de la F.T.: y = tanx
También podemos derivar funciones, aplicando propiedades generales sobre derivación
De manera análoga se puede demostrar las derivadas de las demás funciones trigonométricas; las cuales están resumidas en el cuadro adjunto
Así también se pueden derivar funciones trigonométricas más complejas; ya sea por definición o por propiedades generales.
PROPIEDADES ADICIONALES DE DERIVACIÓN Y APLICACIONES DE LAS DERIVADAS
FUNCIÓN COMPUESTA
EJEMPLO:
Hallar la ecuación de la recta tangente a la gráfica de
F(x) = 2x³+4x² – 5x – 3, en un punto de la curva cuya abscisa es 1
REGLA DE L'HOSPITAL
La regla de L'Hospital reduce la determinación del límite de una función
APLICACIONES DE LA DERIVADA
En ésta sección se exponen las aplicaciones de la derivación a problemas del análisis matemático: estudio de la variación de las funciones, máximos, mínimos, concavidad y convexidad de las curvas, puntos de inflexión. Comenzamos con el estudio de números críticos
FUNCIONES CRECIENTES Y DECRECIENTES ; EL CRITERIO DE LA PRIMERA DERIVADA
La derivada va ha determinar cuando una función es creciente, pues una derivada positiva implica que la pendiente de la gráfica asciende.
Analogamente una derivada negativa implica que la gráfica de la función desciende y una derivada nula en todo un intervalo implica que la función es constante en él.
PROBLEMA 1 :
Si: f(x) = tgx, Calcular: f ' (45°)
PROBLEMA 2 :
Derive: y = f(x) = senx + cosx
A) cosx +senx
B) senx – cosx
C) cosx – senx
D) – senx – cosx
E) senx + 1
PROBLEMA 3 :
Derive: y = f(x) = secx + tanx
A) tanx. f(x)
B) senx.f(x)
C) secxf(x)
D) cot.f(x)
E) –tanx.f(x)
PROBLEMA 4 :
Siendo: y = f(x) = senx – cosx
Hallar: M = f'(x) + f"(x) + f"'(x)
A) senx + cosx
B) senx cosx
C) cosx – senx
D) 2senx – cosx
E) senx – 2cosx
PROBLEMA 5 :
Derive: y = f(x) = Ln(sen²x)
A) tanx
B) cotx
C) 2ctgx
D) 2tanx
E) 2tan2x
PROBLEMA 6 :
Derive: y = f(x) = senxtanx
A) senx + tanx
B) sec + tanx
C) senx + secx
D) senx + tanxsecx
E) senx – secx
PROBLEMA 7 :
Derive: y = f(x) = sen(tanx)
A) sen2x cos(tanx)
B) cos2x cos(tanx)
C) sec2xcos(tgx)
D) –sec2x cos(tanx)
E) csc2x cos(tanx)
PROBLEMA 8 :
Halle la ecuación de la recta tangente a la curva de la función:
y = f(x) = tan2x; en el punto de abscisa: x = 𝛑/8
PROBLEMA 9 :
Dada: y = f(x) = senx + cos2x; halle x que maximize f(x).
RESOLUCIÓN :
Una de las aplicaciones de la derivada permite calcular el máximo o mínimo valor de funciones, para ello se procede hallando la primera derivada e igualando a cero para hallar los puntos críticos y luego se verifica con la segunda derivada.
En la función: y = senx + cos2x
y' = cosx – 2sen2x = 0
⇒ cosx = 2×2senx.cosx
⇒ cosx(1 – 4senx) = 0