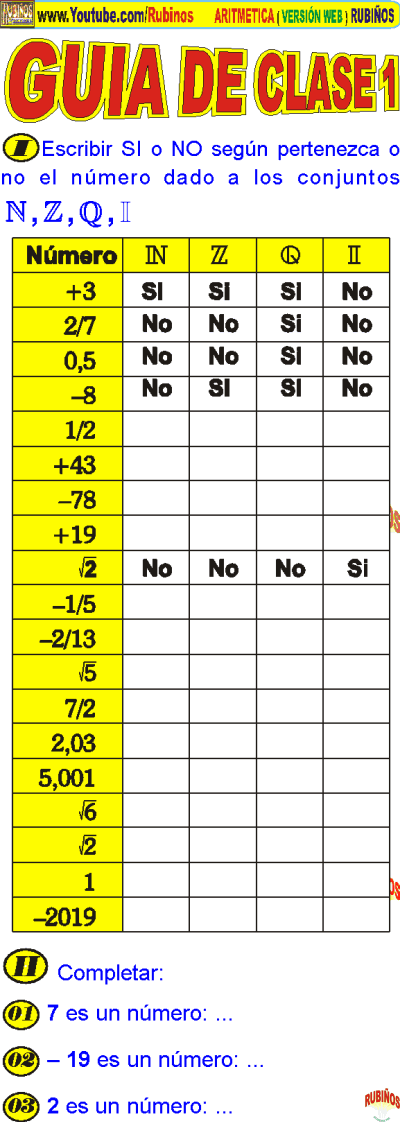
CONJUNTOS NUMÉRICOS EJEMPLOS Y EJERCICIOS RESUELTOS PDF
PROBLEMA 1 :
Determine si cada uno de los enunciados es verdadero V o falso F y escriba la secuencia correcta:
I) {3}={x∈ℕ|1<x<5}
II) Sean A={x∈ℝ|x<0 ∧ x∈ℕ} y
B={x∈ℝ|x∈ℚ ∧ x∈ℂ}, entonces A=B.
III) El conjunto {7,8} tiene cuatro subconjuntos.
A) FVV
B) VVV
C) FVF
D) FFV
E) FFF
RESOLUCIÓN :
Rpta. : "A"
CONJUNTO DE LOS NÚMEROS REALES
El conjunto formado por los racionales y los irracionales se llama conjunto de números reales, y se designa por lR
En la presente secci´on se hace una revisi´on de los principales conjuntos n´umericos, que se necesitan en un primer curso de Matem´atica de nivel universitario. Conjunto de los n´umeros naturales El conjunto de los n´umeros naturales, N , es el primer conjunto de n´umeros conocido y estudiado: N = {1, 2, 3, 4, 5, 6, . . .}
Es un conjunto con un primer elemento, ordenado e infinito. Tambi´en se conoce como el conjunto de los n´umeros enteros positivos.
Claramente el resultado de sumar o multiplicar dos n´umeros naturales, es un n´umero natural. Esta situaci´on no se cumple para el caso de la sustracci´on ni de la divisi´on.
Al no ser la sustracci´on una operaci´on cerrada en N, ecuaciones del tipo x + 7 = 4 no tienen soluci´on en este conjunto, debido a que no existe un n´umero natural que sumado con 7 de como resultado el n´umero 4. Situaciones de este tipo, hacen necesario extender el conjunto de los n´umeros naturales al Conjunto de los n´umeros enteros El conjunto de los n´umeros enteros, Z, es: Z = {. . . ,−4,−3,−2,−1, 0, 1, 2, 3, 4, . . .} En este nuevo conjunto, el problema reci´en planteado tiene soluci´on, ya que el n´umero entero −3 es la soluci´on de la ecuaci´on x + 7 = 4. En el conjunto de los n´umeros enteros, existen algunos conceptos que es necesario tener presente:
• Un n´umero entero a se dice factor o divisor de otro entero b, cuando existe un entero c, tal que: b = a · c. Cuando esto sucede, tambi´en se dice que b es m´ultiplo de a. Por ejemplo: 2 es un factor de 18 (o, 18 es m´ultiplo de 2), pu´es 18 = 2 · 9. • Un n´umero entero p, distinto de 1, se dice primo, cuando sus ´unicos factores son ±1 y ±p. As´ı, por ejemplo, 2, −3, 5, −7 y 11 son n´umeros primos; mientras que, por ejemplo, 4, −6, 8, −10 y 1256 no son n´umeros primos. Cuando un n´umero entero no es primo, se dice compuesto. • Un n´umero entero se dice par, cuando es divisible por 2. As´ı, por ejemplo, −6, 34 y 7772 son n´umeros pares. Si un n´umero entero no es par se dice impar. Observaciones: – Si a es n´umero par, entonces existe un n 2 Z tal que a = 2n. – Si a es n´umero impar, entonces existe un n 2 Z tal que a = 2n + 1. As´ı como el sistema de n´umeros naturales es insuficiente para resolver ciertos tipos de ecuaciones, tambi´en los n´umeros enteros son insuficientes para resolver ecuaciones del tipo ax = b con a y b enteros y a 6= 0. Es claro que esta ecuaci´on s´olo tiene soluci´on en Z, si b es m´ultiplo de a. Para que las ecuaciones de este tipo tengan siempre soluci´on, se hace necesario ampliar el sistema de los n´umeros enteros al Conjunto de los n´umeros racionales El conjunto de los n´umeros racionales, Q, es: Q = {a b / con a y b enteros, b 6= 0} Observaciones: 1. El conjunto de los n´umeros racionales est´a constitu´ıdo por todas las fracciones de enteros, con denominador distinto de 0. 2. Dos racionales a b y c d son iguales siempre y cuando a · d = b · c. Es decir, a b = c d () a · d = b · c 3. Todo n´umero racional a b se puede representar como un n´umero decimal finito o infinito peri´odico. Ello se logra simplemente efectuando la divisi´on entre a y b.
