CONTEO DE FIGURAS Y RECORRIDOS EULERIANOS EJERCICIOS RESUELTOS DE RAZONAMIENTO MATEMÁTICO PREUNIVERSITARIO EN PDF
- CLICK AQUI PARA ver TEORÍA
- CLICK AQUI ver EJERCICIOS RESUELTOS
- CLICK AQUI ver GUIAS CON CLAVES
- CLICK AQUI ver CONTEO DE RUTAS
- CLICK AQUI ver FIGURAS DE UN SOLO TRAZO
- CLICK AQUI ver VIDEOS
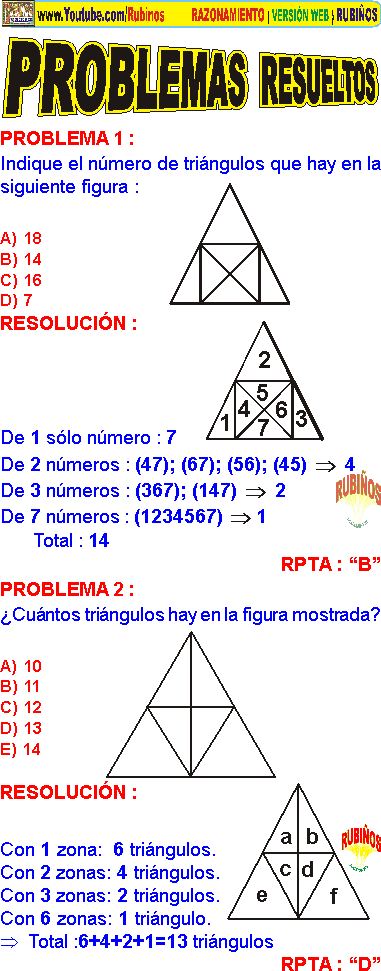
En la figura mostrada. ¿Cuántos triángulos se pueden contar en total?
A) 24
B) 18
C) 20
D) 22
¿Cuántos heptágonos hay?
A) 13
B) 12
C) 11
D) 10
E) 9
¿Cuántos triángulos hay?
A) 5
B) 6
C) 10
D) 9
E) 15
¿Cuántos cuadriláteros hay?
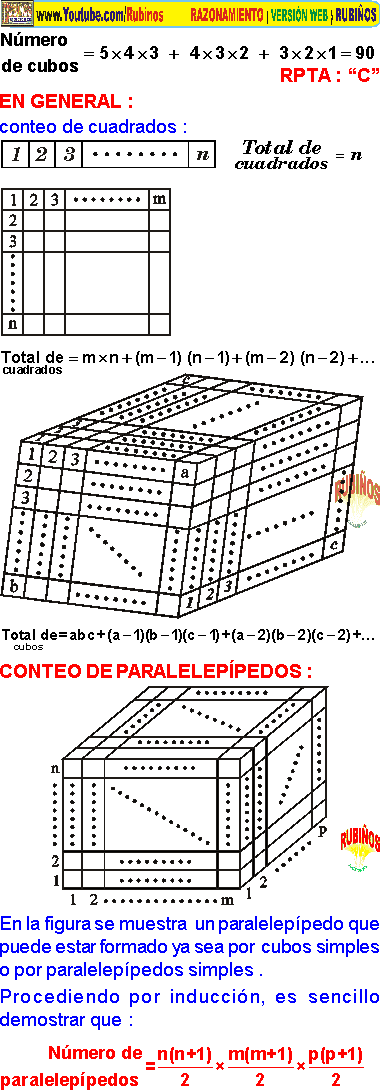
I) El número de cubitos
II) El número de cubos
III) El número de paralelepípedos
IV) El número de paralelepípedos que no son cubos
Indicar la suma de los resultados
A) 960 B) 870 C) 1070 D) 1860 E) 3020
¿Cuántos cuadriláteros hay en la figura mostrada?
A) 316
B) 306
C) 304
D) 300
E) 288
¿Cuántos cuadrados hay?
A) 174
B) 157
C) 89
D) 216
E) 906
¿Cuántas pirámides de base cuadrada se pueden contar en el sólido mostrado?
A) 68
B) 88
C) 98
D) 112
E) 196
¿Cuantos triángulos hay en?
A) 30
B) 90
C) 75
D) 165
E) 225
¿Cuántos triángulos se encuentran que por lo menos tengan un asterisco en su interior?
A) 60
B) 55
C) 50
D) 45
E) 40
¿Cuántas semicircunferencias se encuentran como máximo en la figura mostrada?
A) 2(m + n)
B) 2(m – n)
C) 2mn
En la figura determinar el máximo número de triángulos.
En la figura se muestra la ubicación de las personas M, N, P, Q y R en las esquinas de un parque. Si cada una de las personas se desplaza con la misma rapidez constante, ¿qué personas recorrerán todo el contorno de las áreas en el menor tiempo Posible?
A)M y N
B)M yP
C)N y Q
D)Sólo N
E)Sólo M
El parque mostrado es recorrido cada fin de semana por los vecinos de la urbanización Mira el sol. ¿Cuál es el menor espacio recorrido que hará un vecino si desea recorrer todas las aceras del parque?.(MN = 80, NP = 60 m)
En el gráfico se muestra un prisma recto cuyas bases son hexágonos regulares. Una hormiga camina sobre las aristas de dicho prisma y tarda como mínimo 8 minutos en recorrerlas todas, caminando con rapidez constante. Calcule dicha rapidez de la hormiga.
A) 10 cm/min
B) 11 cm/min
C) 12 cm/min
D) 13 cm/min
E) 14 cm/min
En la figura ABCDEF es un hexágono regular cuyo lado mide 4 cm. Calcular la longitud mínima que debe recorrer la punta del lápiz sin levantarla del papel, para efectuar dicha figura.
A)M y N
B)M yP
C)N y Q
D)Sólo N
E)Sólo M
El parque mostrado es recorrido cada fin de semana por los vecinos de la urbanización Mira el sol. ¿Cuál es el menor espacio recorrido que hará un vecino si desea recorrer todas las aceras del parque?.(MN = 80, NP = 60 m)
En el gráfico se muestra un prisma recto cuyas bases son hexágonos regulares. Una hormiga camina sobre las aristas de dicho prisma y tarda como mínimo 8 minutos en recorrerlas todas, caminando con rapidez constante. Calcule dicha rapidez de la hormiga.
A) 10 cm/min
B) 11 cm/min
C) 12 cm/min
D) 13 cm/min
E) 14 cm/min
En la figura ABCDEF es un hexágono regular cuyo lado mide 4 cm. Calcular la longitud mínima que debe recorrer la punta del lápiz sin levantarla del papel, para efectuar dicha figura.