FUERZA DE ROZAMIENTO EJERCICIOS RESUELTOS PDF
APRENDIZAJES ESPERADOS
☛ Conocer que es rozamiento.
☛ Conocer aquellas situaciones donde se manifiesta la fuerza de rozamiento.
☛ Conocer y entiende el coeficiente de rozamiento estático y cinético.
☛ Cuantificar los dos tipos de fuerza de rozamiento entre dos superficies.
☛ Calcular fuerza de rozamiento en sistemas estáticos y dinámicos.
☛ Desarrollar ejercicios de la primera condición de equilibrio mecánico incluyendo la fuerza de rozamiento.
En nuestra vida cotidiana estamos relacionados con el rozamiento o fricción que entre otras cosas nos permite caminar sin resbalarnos, coger objetos sin que resbalen de nuestras manos, permiten frenar o cambiar de dirección a los autos, etc.
¿Qué es una fuerza de rozamiento?
Es aquella fuerza que surge entre dos superficies ásperas en contacto el cual se opone a la tendencia al deslizamiento o al deslizamiento de los cuerpos.
En la dirección perpendicular a las superficies en contacto, hay una fuerza que no permite que el bloque se hunda, a dicha fuerza la denominaremos fuerza normal.
A continuación ampliaremos más sobre el estudio de esta fuerza de rozamiento
Recordemos las fuerzas que se manifiestan en la superficie de contacto entre dos cuerpos a partir del diagrama del cuerpo libre del cuerpo
𝑖) Para el bloque liso
La fuerza de reacción es perpendicular a las superficies de contacto, debido a la existencia de superficies lisas.
𝑖𝑖) Para el bloque en reposo
La fuerza de reacción no es perpendicular a las superficies en contacto ninguna de las superficies en contacto son lisas (superficies rugosas)
A la suma de aquellas fuerzas microscópicas y tangenciales que se producen en la región de contacto se le llama fuerza de rozamiento
¿CUÁL ES LA DIFERENCIA ENTRE UNA SUPERFICIE LISA Y UNA SUPERFICIE RUGOSA?
SUPERFICIE LISA
Entendemos como superficie lisa, aquella superficie ideal que no presenta asperezas (irregularidades).
SUPERFICIE RUGOSA
Son todas las superficies que están en nuestro entorno, estas superficies se caracterizan por presentar asperezas, grietas (irregularidades).
Para notar las irregularidades de una superficie, se necesita de una vista ampliada mediante un microscopio.
FUERZA DE ROZAMIENTO POR DESLIZAMIENTO
Estas fuerzas de rozamiento se dan entre dos superficies sólidas, y se manifiestan dos tipos de fuerza de rozamiento.
FUERZA DE ROZAMIENTO ESTÁTICO
Esta fuerza surge entre dos superficies ásperas, cuando una de ellas tiende a deslizar respecto a la otra.
Consideremos el ropero en reposo que se intenta deslizar aplicando una fuerza que gradualmente va aumentando.
μs : coeficiente de rozamiento estático ; es un número que indica el grado de asperezas de las superficies en contacto
FUERZA DE ROZAMIENTO CINÉTICO
Esta fuerza surge entre dos superficies ásperas, cuando una de ellas desliza respecto a la otra.
Su dirección se opone al deslizamiento del cuerpo
COEFICIENTE DE ROZAMIENTO
Se trata de un número que caracteriza el grado de rugosidad entre cada dos superficies sólidas en contacto.
Depende de varios factores: el acabado de las superficies, la temperatura, la presencia de lubricantes, entre otros.
Hay dos tipos de coeficiente de rozamiento:
– coeficiente de rozamiento estático
– coeficiente de rozamiento cinético
Se verifica que en la mayoría de los casos el coeficiente de rozamiento estático es mayor que el coeficiente de rozamiento cinético
LEYES Y CARACTERÍSTICAS DE ROZAMIENTO
Los resultados de un gran número de experiencias sobre el rozamiento en superficies secas, publicadas por Coulomb en 1781, proporcionaron las primeras informaciones sobre las leyes del rozamiento, obteniéndose las siguientes leyes:
☛ La fuerza máxima de rozamiento que puede producirse es proporcional a la fuerza normal entre las superficies en contacto.
☛ Esta fuerza máxima es independiente del tamaño de la superficie de contacto.
☛ La fuerza límite de rozamiento estático es mayor que la fuerza de rozamiento cinético, siempre que actúe la misma fuerza normal.
☛ El coeficiente de rozamiento cinético es menor que el coeficiente de rozamiento estático.
☛ La fuerza de rozamiento cinético es independiente de la velocidad relativa de los cuerpos en contacto.
☛ La fuerza de rozamiento surge cuando un cuerpo resbala o tiende a resbalar sobre una superficie, siendo ambas superficies ásperas.
☛ Los coeficientes de rozamiento son dos números que denotan el grado de aspereza entre dos superficies en contacto.
☛ El coeficiente de rozamiento estático es aproximadamente 25% más pequeño que el coeficiente de rozamiento cinético .
☛ La fuerza de reacción , es el vector resultante de la fuerza de rozamiento y la fuerza normal.
PROBLEMA 1 :
Respecto de la fuerza de fricción indicar la veracidad (V) o falsedad (F) de las proposiciones siguientes:
I) Siempre tiene sentido contrario al del movimiento del cuerpo sobre el que actúa.
II) La fricción estática desgasta o destruye las superficies sobre las que actúa.
III) Los coeficientes de fricción no pueden tomar valores mayores que uno.
A) VVV
B) FFF
C) VFV
D) FVF
E) VFF
RESOLUCIÓN :
I) Falsa , ya que la fuerza de rozamiento cinético, siempre tiene sentido contrario al movimiento del cuerpo sobre el que actúa, en cambio la fuerza de rozamiento estático actúa sobre un cuerpo en reposo relativo, en este caso la fuerza de rozamiento se opone al sentido del posible movimiento.
II) Falsa , dado que la fricción cinética es la que desgasta o destruye las superficies sobre la cual actúa.
III) Falsa , experimentalmente se ha demostrado que los coeficientes de rozamiento están entre 0 y 1, sin embargo hay excepciones en la que pueden ser mayor que 1.
Rpta. : "B"
PROBLEMA 2 :
Si el bloque de la figura, bajo la acción de las fuerzas presentes, sube por el plano con una aceleración constante de 2,5m/s² ; determine el coeficiente de rozamiento cinético entre las superficies del bloque y el plano.
A) 0,14
B) 0,20
C) 0,25
D) 0,40
E) 0,75
RESOLUCIÓN :
Rpta. : "A"
PRACTICA PROPUESTA
PROBLEMA 1 :
Se requiere de una fuerza horizontal de 10N para desplazar una caja de 3kg de masa sobre un piso horizontal a una velocidad constante de 0,20 m/s. ¿Cuál es la magnitud de la fuerza de fricción que se opone al movimiento de la caja, (en Newtons)?
A) 10
B) 15
C) 20
D) 30
Rpta. : "A"
PROBLEMA 2 :
Un ladrillo de masa m es lanzado horizontal sobre una superficie horizontal con una rapidez de 10m/s. Si entre el ladrillo y la superficie el coeficiente de rozamiento cinético, es 0,4 ; determine el módulo de la aceleración del movimiento de dicho ladrillo
(g = 10 m/s²).
A) 2 m/s²
B) 3 m/s²
C) 4m/s²
D) 1m/s²
E) 3m/s²
Rpta. : "C"
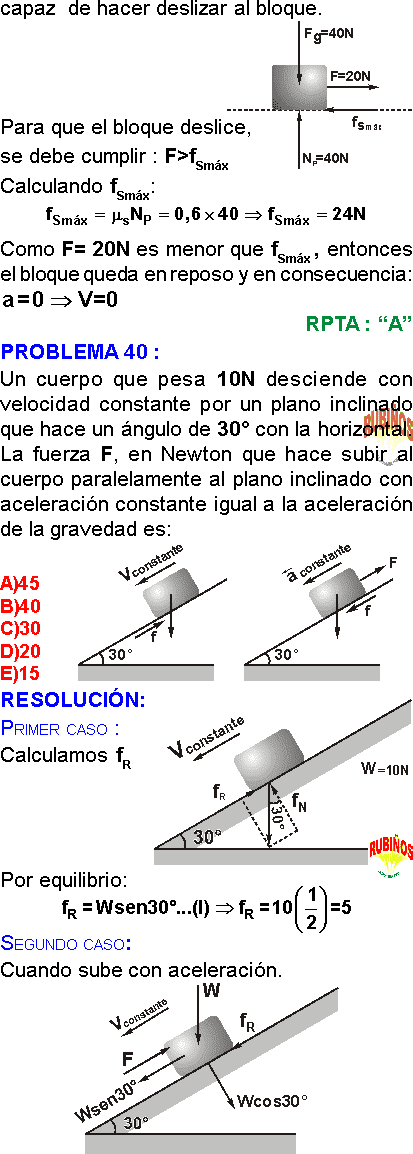
PROBLEMA 3 :
Un carrito se desplaza (con respecto a Tierra) con aceleración de 5m/s2 hacia la derecha. Sobre él reposa un bloque de 1,2 kg de masa. La fuerza que actúa sobre el bloque será (en Newtons). (g = aceleración de la gravedad)
A) Falta conocer el coeficiente de rozamiento entre el bloque y el carrito.
B) 6g
C) 5
D) 1,2
E) 6N
Rpta. : "E"
PROBLEMA 4 :
Un bloque de 10N se coloca sobre un plano inclinado a 53°. Si la fricción es de 2N, ¿con qué fuerza horizontal se deberá empujar al bloque para que éste se deslice hacia abajo del plano con velocidad constante?
A) 2N
B) 5N
C) 7,5N
D) 8N
E) 10N
Rpta. : "E"
PROBLEMA 5 :
Se jala un bloque de masa de 4kg apoyado sobre una superficie horizontal rugosa (coeficientes de fricción estático y dinámico 0,2 y 0,1 respectivamente) aplicando una fuerza horizontal de magnitud igual a 9 Newton. En estas condiciones, ¿cuánto valdrá el ángulo que forman la reacción total del plano sobre el bloque con la línea normal al plano horizontal?
(tome g = 10 m/s²).
A) Tg−¹(0,1)
B) Tg−¹(0,2)
C) Tg−¹(0,3)
D) 𝛑/4
E) 𝛑/2
Rpta. : "A"
PROBLEMA 6 :
Un bloque de 1kg se coloca sobre un plano inclinado que forma un ángulo de 37° con la horizontal. Al soltarlo con velocidad cero se desliza una distancia de 40cm en 10s. ¿Cuál es el valor aproximado del coeficiente de fricción?.
(Considerar g = 10 m/s²)
A) 0,59
B) 0,65
C) 0,70
D) 0,74
E) 0
Rpta. : "D"
PROBLEMA 7 :
Un ladrillo de 4kg, en reposo sobre una superficie horizontal, es empujado con una fuerza horizontal F=20N. Si los coeficientes de rozamiento entre el ladrillo y la superficie son: 0,4 y 0,6. determine la rapidez del ladrillo 5s después de empezar a ejercer la fuerza F.
(g=10 m/s²).
A)cero
B) 1 m/s
C) 2 m/s
D) 3 m/s
E) 5 m/s
Rpta. : "A"
PROBLEMA 8 :
Un bloque se desliza sin fricción desde el reposo hacia abajo por un plano inclinado que hace un ángulo de 45° con la horizontal. Cuando se desliza sobre otro plano que tiene la misma inclinación que el anterior pero con un coeficiente de fricción μ, también partiendo desde el reposo, el tiempo empleado en recorrer la misma longitud es el doble. Calcular el valor de μ.
A) 1/4
B) 1/3
C) 4/9
D) 3/4
E) 4/3
Rpta. : "D"
PROBLEMA 9 :
Con respecto a la fuerza de rozamiento marque verdadero (V) o falso (F), según corresponda.
( ) La fuerza de rozamiento es una componente de la fuerza de reacción, con dirección tangencial a la superficie en contacto.
( ) La fuerza de rozamiento se opone siempre al movimiento relativo del cuerpo respecto de la superficie en contacto.
( ) La fuerza de rozamiento estático es variable desde cero hasta un valor máximo cuando el cuerpo está a punto de moverse.
A) VVF
B) VFF
C) FVV
D) VFV
E) VVV
PROBLEMA 10 :
Para que exista la fuerza de rozamiento o fricción entre dos superficies en contacto.
¿Qué condiciones deben darse?
I. Ambas deben ser ásperas e intentar resbalar entre sí.
II. Una debe ser lisa y la otra áspera, y resbalar entre sí.
III. Ambas deben ser rugosas y resbalar entre sí.
A) solo I
B) solo II
C) I y II
D) II y III
E) I y III
PROBLEMA 11 :
Un bloque de 10 N se coloca sobre un plano inclinado (θ=53º). Si la fricción es de 2 N, ¿con qué fuerza horizontal se deberá empujar al bloque para que este se deslice hacia abajo del plano con velocidad constante?
A) 10 N
B) 20 N
C) 30 N
D) 40 N
E) 50 N
Rpta. : "A"
PROBLEMA 12 :
Una forma práctica de encontrar el coeficiente de rozamiento entre dos cuerpos es usando un plano inclinado y determinando la tangente del ángulo que forma el plano con la horizontal en aquel momento en que el bloque está a punto de deslizar sobre el plano. Considere un bloque que reposa sobre un plano cuyo coeficiente de fricción es 0,5. Entonces el máximo ángulo que puede inclinarse el plano es
A) 37°
B) 53°
C) 26,5°
D) 16°
E) 8°
Rpta. : "C"
PROBLEMA 13 :
Cuando lanzamos un cuerpo sobre un piso áspero, el cuerpo se detiene no porque dejamos de aplicarle una fuerza sino más bien debido a la fuerza de fricción que le ejerce el piso. Entonces si luego de haber lanzado un bloque de 2 kg se tiene que la magnitud de la reacción del piso es 25 N, determine el coeficiente de rozamiento cinético.
( g= 10 m/s).
A) 0,5
B) 0,6
C) 0,7
D) 0,75
E) 0,25
Rpta. : "D"
PROBLEMA 14 :
La mayoría de las superficies, aun las que se consideran pulidas, son extremadamente rugosas a escala microscópica. Es la fuerza de rozamiento la que evita que un cuerpo deslice sobre otro. Considere un bloque de 4 kg que reposa en un piso horizontal con coeficiente de fricción 0,8. Entonces si le aplicamos una fuerza horizontal de 30 N, indique la magnitud de la reacción del piso.
(g=10 m/s²).
A) 32 N
B) 80 N
C) 50 N
D) 30 N
E) 40 N
Rpta. : "C"
El rozamiento entre dos superficies en contacto ha sido aprovechado por nuestros antepasados más remotos para hacer fuego frotando maderas.
En nuestra época, el rozamiento tiene una gran importancia económica, se estima que si se le prestase mayor atención se podría ahorrar muchísima energía y recursos económicos. Históricamente, el estudio del rozamiento comienza con Leonardo da Vinci que dedujo las leyes que gobiernan el movimiento de un bloque rectangular que desliza sobre una superficie plana. Sin embargo, este estudio pasó desapercibido.
En el siglo XVII Guillaume Amontons, físico francés, redescubrió las leyes del rozamiento estudiando el deslizamiento seco de dos superficies planas.
Las conclusiones de Amontons son esencialmente las que estudiamos en los libros de Física General:
☛ La fuerza de rozamiento se opone al movimiento de un bloque que desliza sobre un plano.
☛ La fuerza de rozamiento es proporcional a la fuerza normal que ejerce el plano sobre el bloque.
☛ La fuerza de rozamiento no depende del área aparente de contacto.
El científico francés Coulomb añadió una propiedad más
☛ Una vez empezado el movimiento, la fuerza de rozamiento es independiente de la velocidad.
La mayoría de las superficies, aún las que se consideran pulidas son extremadamente rugosas a escala microscópica. Los picos de las dos superficies que se ponen en contacto determinan el área real de contacto que es una pequeña proporción del área aparente de contacto (el área de la base del bloque). El área real de contacto aumenta cuando aumenta la presión (la fuerza normal) ya que los picos se deforman.
Los metales tienden a soldarse en frío, debido a las fuerzas de atracción que ligan a las moléculas de una superficie con las moléculas de la otra. Estas soldaduras tienen que romperse para que el deslizamiento se presente. Además, existe siempre la incrustación de los picos con los valles. Este es el origen del rozamiento estático.
Cuando el bloque desliza sobre el plano, las soldaduras en frío se rompen y se rehacen constantemente. Pero la cantidad de soldaduras que haya en cualquier momento se reduce por debajo del valor estático, de modo que el coeficiente de rozamiento cinético es menor que el coeficiente de rozamiento estático.
Finalmente, la presencia de aceite o de grasa en las superficies en contacto evita las soldaduras al revestirlas de un material inerte.