RAZONES Y PROPORCIONES PROBLEMAS RESUELTOS PDF ARITMÉTICA
OBJETIVOS
☛ Identificar las magnitudes de nuestro entorno y medir su intensidad para expresarla cuantitativamente.
☛ Establecer una comparación entre las medidas de las magnitudes, mediante las operaciones de sustracción y división.
☛ Reconocer una Razón Aritmética de una Razón Geométrica y relacionar cada una para obtener la proporción Aritmética y proporción Geométrica.
☛ Aplicar las propiedades en la resolución de los problemas que se presentan en la vida cotidiana.
SUBTEMAS:
☛ Definición de Razón
☛ Clases de Razón : aritmética y geométrica
☛ Interpretación de las razones
☛ Aplicación de las razones en problemas de edades
☛ Aplicación en problemas de reuniones
☛ Aplicación en problemas de mezclas y en problemas de móviles.
☛ Igualdad de razones geométricas equivalentes: definición
☛ Propiedades de las razones (suma, diferencia y producto)
☛ Serie de razones geométricas continuas (SRGE)
☛ Proporción: definición
☛ Clases de proporción (aritmética y geométrica)
☛ Tipos de proporción (discreta y continua)
☛ Razón geométrica
☛ Proporción geométrica
☛ Situaciones de homogenización e interpretación de textos.
Las situaciones matemáticas más frecuentes de todos los tiempos ha sido, sin duda, la de relacionar dos cantidades; durante nuestro proceso de aprendizaje lo hemos hecho al sumarlas, restarlas, multiplicarlas y dividirlas.
De manera muy particular, al relacionarlas mediante la sustracción y la división, estamos comparándolas.
Así podemos comparar:
• Los precios de dos libros..
• Las velocidades de tres motos.
• Las alturas de dos árboles.
PRIMERA PRACTICA
EJERCICIO 1 :
La razón de 30 y 45 es:
A) 5/7
B) 5/3
C) 2/3
D) 1/5
EJERCICIO 2 :
La razón entre 20 y 35 es:
A) 0,75
B) 0,57
C) 0,45
D) 0,35
EJERCICIO 3 :
La razón 1 a 5 equivale a:
A) 1
B) 0,5
C) 0,2
D) 10
EJERCICIO 4 :
La razón entre 7,5 y 1,5 es:
A) 3
B) 4
C) 5
D) 6
EJERCICIO 5 :
¿Cuál es la razón de 20 y 5?
A) 2
B) 20
C) 4
D) 2/5
EJERCICIO 6 :
La estatura de un señor es 1,80 m y la de su hijo 1,10 m. ¿Cuál es la razón de la estatura de su hijo respecto a la del padre?
A) 0,63
B) 0,61
C) 0,66
D) 0,62
EJERCICIO 7 :
Hallar un número que excede al mayor número par de 3 cifras en 332.
A) 1330
B) 1500
C) 1600
D) 1200
E) 1800
EJERCICIO 8 :
Las edades de Susana y María están en la relación de 3 a 5, si dentro de 8 años sus edades sumarán 48 años. Hallar la edad de María.
A) 28
B) 18
C) 42
D) 46
E) 20
EJERCICIO 9 :
La razón aritmética de 2 números es 600 y su razón geométrica es 7/3. Hallar el menor de dichos números.
A) 200
B) 180
C) 120
D) 150
E) 50
EJERCICIO 10 :
Si la relación entre dos números es como 5 es a 3, calcula el valor del mayor, sabiendo que su suma es igual a 40.
A) 10
B) 15
C) 20
D) 25
EJERCICIO 11 :
La suma de dos números es 27. si su razón aritmética es 11, el número menor es:
A) 7
B) 4
C) 9
D) 8
EJERCICIO 12 :
Luz tiene 49 años y Eva 13. ¿En cuántos años más, la relación entre sus edades será de 16 a 7?
A) 15
B) 10
C) 12
D) 16
EJERCICIO 13 :
Los términos de una razón geométrica suman 80. Calcula diferencia si la razón es igual a 2,333…
A) 30
B) 32
C) 34
D) 36
EJERCICIO 14 :
Dos números están en la relación de 5 a 7, si la suma de ellos es 360; hallar el menor.
A) 40
B) 150
C) 21
D) 180
E) 120
EJERCICIO 15 :
En un Salón de clase las cantidades de varones y mujeres están en la relación de 4 a 9. si la razón aritmética de dichas cantidades es 15, ¿Cuántos alumnos hay en dicha clase?
A) 24
B) 36
C) 13
D) 39
E) 42
EJERCICIO 16 :
El producto de dos números es 196 y su razón geométricas es 4/3, hallar el mayor.
A) 24
B) 18
C) 16
D) 28
E) 14
EJERCICIO 17 :
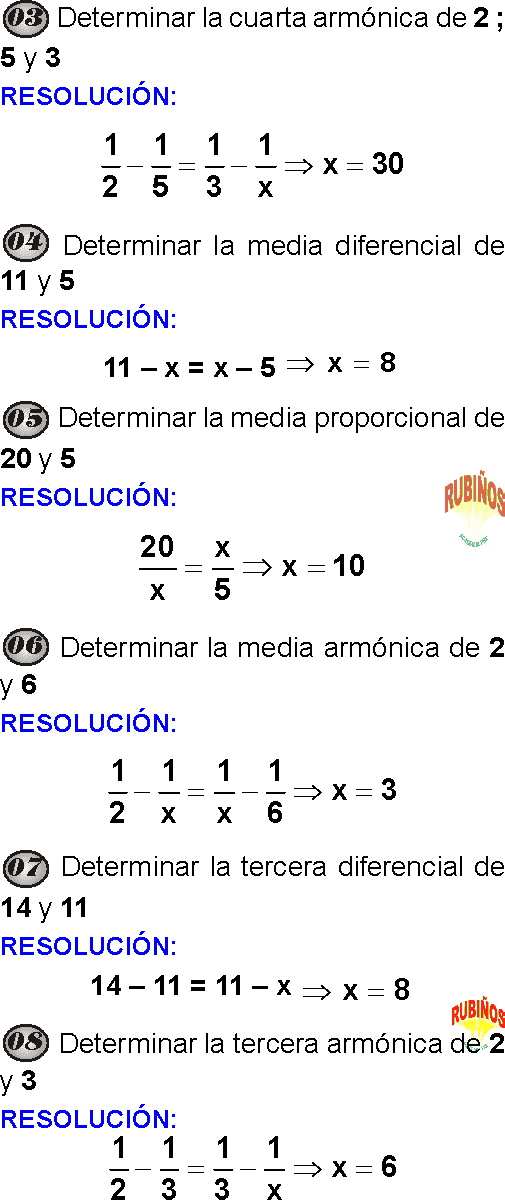
Determinar la cuarta diferencial de 72 ; 28 y 57.
A) 13
B) 23
C) 33
D) 43
E) 53
EJERCICIO 18 :
Determinar la cuarta diferencial de 85 ; 18 y 93.
A) 11
B) 27
C) 31
D) 37
E) 41
EJERCICIO 19 :
Determinar la media proporcional de 7 y 28.
A) 14
B) 21
C) 35
D) 18
E) 7
EJERCICIO 20 :
Determinar la media proporcional de 16 y 49.
A) 21
B) 28
C) 33
D) 36
E) 42
EJERCICIO 21 :
Determinar la tercera proporcional de 8 y12.
A) 18
B) 9
C) 4
D) 14
E) 20
EJERCICIO 22 :
Determinar la tercera proporcional de 24 y 36.
A) 62
B) 54
C) 42
D) 26
E) 12
SEGUNDA PRACTICA
EJERCICIO 1 :
Halla a y b en: a/15=b/12 ; si a – b=9.
A) 6; 3
B) 2; 7
C) 5; 4
D) 4; 5
EJERCICIO 2 :
Halla a y b en:18/a=9/b ; si a – b = 3.
A) 6; 4
B) 5; 2
C) 6; 3
D) 7; 5
EJERCICIO 3 :
Las edades de un hijo y de su padre están en la relación de 1 a 5. Si la suma de sus edades es de 42 años, ¿cuál es la edad del padre?
A) 30
B) 35
C) 40
D) 45
EJERCICIO 4 :
En una fiesta se observa que las mujeres son el triple de los varones y la razón aritmética de dichas cantidades es 28. ¿Cuántas personas asistieron a dicha fiesta?
A) 14
B) 84
C) 56
D) 80
E) 72
EJERCICIO 5 :
En un salón de clases por cada 5 varones hay 3 mujeres, además se sabe que hay 8 varones más, ¿cuántos alumnos hay en dicho salón?
A) 20
B) 32
C) 40
D) 60
E) 64
EJERCICIO 8 :
Determinar la cuarta diferencial de 632 ; 541 y 214.
A) 108
B) 113
C) 123
D) 256
E) 305
EJERCICIO 9 :
Determinar la cuarta diferencial de 13; 7 y 91.
A) 7
B) 14
C) 21
D) 49
E) 85
EJERCICIO 10 :
La razón de dos números es 4/7 y su suma es 286. Hallar el mayor de los números
a) 44
b) 77
c) 55
d) 66
e) 99
EJERCICIO 11 :
Dos números son entre sí como 9 es a 16, si su suma es 1050. Hallar el menor de los números.
a) 225
b) 175
c) 400
d) 450
e) 600
EJERCICIO 12 :
La diferencia de 2 números es 244 y están en la relación de 7 a 3. ¿Cuál es la suma de los números?
a) 1440
b) 1220
c) 1700
d) 1400
e) 1500
EJERCICIO 13 :
Dos números son proporcionales a 2 y 5 y su producto es 9000. Hallar su diferencia.
a) 45
b) 60
c) 75
d) 90
e) 108
EJERCICIO 14 :
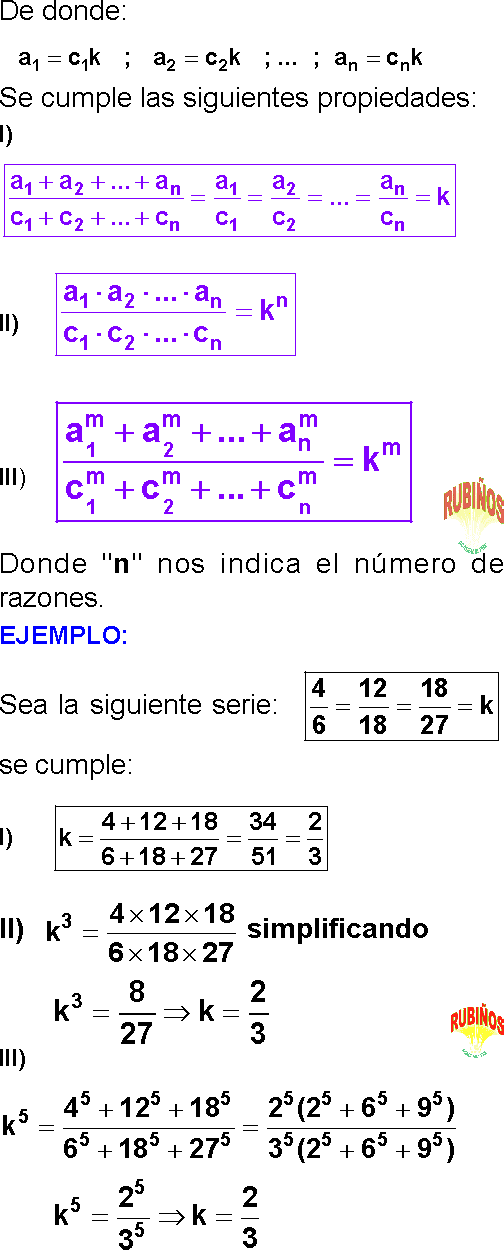
En una serie de razones iguales, los antecedentes son 3 ; 5 y 7 y el producto de los consecuentes es 2835. Hallar el consecuente menor
a) 2
b) 5
c) 6
d) 8
e) 9
EJERCICIO 15 :
En una serie de razones equivalentes los antecedentes son 2 ; 5 y 8. El producto de los consecuentes es 5120. Hallar el consecuente mayor.
a) 36
b) 32
c) 28
d) 24
e) 20
EJERCICIO 16 :
En una serie de razones equivalentes los consecuentes son 12; 5 y 9. Si la suma de los antecedentes es 208. Hallar el antecedente mayor.
a) 100
b) 96
c) 48
d) 72
e) 60
EJERCICIO 17 :
En una serie de razones equivalentes los consecuentes son 15; 20; 18; 25. Si la suma de los antecedentes es 234. Hallar la diferencia entre el mayor y menor antecedente.
a) 24
b) 28
c) 30
d) 12
e) 3
EJERCICIO 18 :
Los antecedentes de varias razones equivalentes son 6; 10; 12 y 8. Si el producto de los consecuentes es 29160. Hallar la suma de los consecuentes.
a) 54
b) 36
c) 72
d) 48
e) 96
EJERCICIO 19 :
En una serie de razones equivalentes los antecedentes son 3; 4; 5 y 7. Si el producto de los consecuentes es 262500. Hallar la diferencia entre el mayor y menor consecuente.
a) 28
b) 25
c) 18
d) 15
e) 20
EJERCICIO 20 :
Las medidas de los ángulos de un triángulo son entre sí como los números 5; 3 y 7. ¿Cuál es el ángulo que no pertenece a este triángulo.
a) 60°
b) 30°
c) 36°
d) 84°
EJERCICIO 21 :
Tres números son entre sí como 7; 9 y 10. Tales que el segundo más el triple del tercero suman 156. Hallar el primer número.
a) 24
b) 30
c) 28
d) 32
e) 45
EJERCICIO 22 :
La suma, la diferencia y el producto de dos números están en la misma relación que los números 6; 4 y 25. Hallar los números.
A) 5 y 25
B) 4 y 20
C) 15 y 30
D) 12 y 15
EJERCICIO 23 :
La suma, la diferencia y el producto de dos números están en la misma relación que los números 5; 3 y 16. Hallar el número mayor.
a) 18
b) 16
c) 20
d) 24
e) 25
TERCERA PRACTICA
PREGUNTA 1 :
Las edades de Juan y Rocío están en relación de 5 a 9 y la suma de ellas es 84. ¿Qué edad tiene Juan?
A) 20 años
B) 30
C) 40
D) 45
E) 60
Rpta. : "B"
PREGUNTA 2 :
Calcular la cuarta diferencial de los precios de tres artículos que son S/.50 , S/.34 y S/.29.
A) 12
B) 21
C) 13
D) 18
E) 17
Rpta. : "C"
PREGUNTA 3 :
Calcule la cuarta proporcional de las estaturas de 3 estudiantes y que son: 1,6 m; 1,2m y 1,4m.
A) 1
B) 2,03
C) 2,01
D) 1,05
E) 3
Rpta. : "D"
PREGUNTA 4 :
La razón geométrica de dos números vale 4/7 y su razón aritmética es 45. Determina el menor de los números.
A) 50
B) 45
C) 60
D) 70
E) 52
Rpta. : "C"
PREGUNTA 5 :
Tres números son entre sí como 4 ; 7 y 11, y la suma del menor con el mayor de dichos números es 105. Determinar el menor de estos números.
A) 49
B) 14
C) 24
D) 30
E) 28
Rpta. : "E"
PREGUNTA 6 :
Tres números están en la misma relación que 5 ; 9 y 13. Si la suma de ellos es 216. Indica el mayor de ellos .
A) 102
B) 88
C) 104
D) 96
E) 108
Rpta. : "C"
PREGUNTA 7 :
En una proporción geométrica se sabe que el producto de extremos es 600. Si los términos medios son consecutivos. ¿Cuál es la suma de los términos medios?
A) 94
B) 49
C) 24
D) 25
E) 78
Rpta. : "B"
PREGUNTA 8 :
En una proporción continua la diferencia de los extremos es 20 y el valor de la constante es 2/3. Determinar la media proporcional.
A) 42
B) 21
C) 24
D) 20
E) 27
Rpta. : "C"
PREGUNTA 9 :
La media diferencial de una proporción es 24. determinar la razón de la proporción, si el primer extremo es el doble del segundo.
A) 6
B) 8
C) 10
D) 16
E) 12
Rpta. : "B"
PREGUNTA 10:
La relación entre el número de pasajeros de dos micros es de 7 a 5; si bajan 4 pasajeros de uno y suben al otro, se iguala el número de pasajeros en ambos , ¿cuántos pasajeros llevan entre ambos?
a) 54
b)36
c)72
d)60
e) 48
Rpta. : "E"
PREGUNTA 11:
La media geométrica de una proporción es 15. Hallar la suma de los extremos, si la razón de la proporción es 1/3.
A) 40
B) 50
C) 60
D) 45
E) 35
Rpta. : "B"
PREGUNTA 12:
El producto de los cuatro términos de una proporción geométrica continua es 20 736. Si la razón de la proporción es menor que 1 y la suma de los extremos es 30, determinar el segundo extremo.
A) 12
B) 20
C) 28
D) 32
E) 24
Rpta. : "E"
PREGUNTA 13:
Los consecuentes de una serie de razones iguales son respectivamente 2 ; 9 y 13. Si la suma de los antecedentes es 480, ¿Cuál es la suma de los dos primeros antecedentes?
A) 200
B) 180
C) 220
D) 170
E) 280
Rpta. : "C"
PREGUNTA 14:
Los antecedentes de una serie de razones iguales son respectivamente 3 ; 7 ; 9 y 5. Si el producto de los consecuentes es 15 120, calcular la suma de los tres primeros consecuentes.
A) 38
B) 43
C) 72
D) 80
E) 92
Rpta. : "A"
PREGUNTA 15:
La suma de los 4 términos de una proporción geométrica continua es a la diferencia de sus extremos como 3 es a 1. ¿Cuál es la razón geométrica del extremo mayor al extremo menor?
a) 4:1
b) 3:2
c) 3:5
d) 1:2
e) 2:3
Rpta. : "A"
PREGUNTA 16:
La suma, la diferencia y el producto de dos números están en la misma relación que los números 5; 3 y 16. Determinar la suma de dichos números.
A) 30
B) 20
C) 45
D) 15
E) 12
Rpta. : "B"
PREGUNTA 17:
A una fiesta asisten 140 personas entre hombres y mujeres. Por cada 3 mujeres hay 4 hombres. Si se retiran 20 parejas. ¿Cuál es la razón entre el número de mujeres y el número de hombres que se quedan en la fiesta?
a) 1:2
b) 2:3
c) 3:4
d) 3:5
e) 4:1
Rpta. : "B"
PREGUNTA 18:
Para envasar 15000 litros de aceite se dispone de botellas de 1/2 litro, 1 litro y 5 litros. Por cada botella de 5 litros, hay 10 de un litro y 20 de medio litro. Al terminar de envasar el aceite, no sobra ninguna botella vacía. ¿Cuántas botellas había en total ?.
A) 18000
B) 27000
C) 18600
D) 30000
E) 240
Rpta. : "C"
PREGUNTA 19:
En un colegio estudian 910 alumnos entre hombres y mujeres en la proporción de 3 a 10. Luego un grupo de ellos van de paseo y se contratan algunos «buses» , si en cada bus viajan 60 mujeres y ‘‘x’’ hombres , observándose que el número de hombres es al número de mujeres (que van de paseo) como 5 es a 12 ¿cuántos alumnos (en total) como mínimo no van de paseo?
A) 10
B) 60
C) 120
D) 130
E) 230
Rpta. : "E"
PREGUNTA 20:
Un piloto observa que el número de aviones es al número de barcos como 7 es a 6, pero a la vez el timonel nota que el número de aviones es al número de barcos como 8 es a 5. Hallar la diferencia entre el número de aviones y barcos.
a) 2
b) 4
c) 1
d) 6
e) 7
Rpta. : "A"
PREGUNTA 21:
La suma, la diferencia y el producto de dos números, están en la misma relación que los números 10; 4 y 63 respectivamente. ¿Cuál es el mayor de ellos?
a) 30
b) 28
c) 25
d) 23
e) 21
Rpta. : "E"
PREGUNTA 22:
Un asunto fue sometido a votación de 600 personas y se perdió; habiendo votado de nuevo las mismas personas sobre el mismo asunto, fue ganado el caso por el doble de votos por el que se había perdido la primera vez, y la nueva mayoría fue con respecto a la anterior como 8 es a 7. ¿Cuántas personas cambiaron de opinión?.
A) 100
B) 110
C) 120
D) 140
E) 150
Rpta. : "E"
PREGUNTA 23:
La diferencia de dos números es 10. Si la diferencia de las razones geométricas que se pueden formar con dichos numeras es 5/6. Hallar la media armónica de los mismos.
a) 11
b) 16
c) 20
d) 22
e) 24
Rpta. : "E"
PREGUNTA 24:
Determinar la tercia proporcional entre la media proporcional de 9; 16 y la cuarta proporcional de 10;15 y 14.
a) 38
b) 36,75
c) 40
d) 34,25
e) 32,5
Rpta. : "B"
PREGUNTA 25:
La suma de los 4 términos de una proporción geométrica continua es 25. Si el producto de dichos términos es 1296, calcular el mayor de los extremos.
a) 9
b) 8
c) 7
d) 6
e) 5
Rpta. : "A"
PREGUNTA 26:
La suma de los 4 términos de una proporción es 65; cada uno de los 3 últimos términos es 2/3 del precedente. ¿Cuál es el último término?
a) 4
b) 6
c) 8
d) 7
e) 10
Rpta. : "C"
PREGUNTA 27:
En una serie de 4 razones geométricas iguales se sabe que la suma de cuadrados de los consecuentes menos la suma de cuadrados de los antecedentes es 1296 y que la suma de las 2 últimas razones es 10/7. Determinar la suma de cuadrados de los antecedentes.
a) 850
b) 960
c) 1100
d) 1350
e) 1400
Rpta. : "D"
PREGUNTA 28:
El producto de tres números enteros positivos es 21952. Si el primero es al segundo como éste es al tercero , entonces uno de los números es:
a) 12
b) 39
c) 88
d) 196
e) 304
Rpta. : "D"
PREGUNTA 29:
En una serie de cuatro razones geométricas continuas, la suma de los términos no extremos es 228, además la diferencia del cuarto término y el tercer consecuente es 12. Calcular la razón aritmética de los extremos. Los términos son enteros.
A) 65
B) 60
C) 56
D) 54
E) 50
Rpta. : "A"
PREGUNTA 30:
Se tiene un cierto número de bolas blancas, rojas y azules, donde se cumple que por cada 4 blancas hay 5 rojas, y por cada 7 rojas hay 11 azules. Si la cantidad de azules excede a las rojas en 140. ¿En cuánto exceden las bolas azules respecto a las bolas blancas?
A) 49
B) 196
C) 198
D) 189
E) 169
Rpta. : "D"
PREGUNTA 31:
En una proporción geométrica continua la suma de los cuatro términos es 700 y la diferencia entre los extremos es 280. Hallar la suma de extremos.
A) 194
B) 206
C) 406
D) 309
E) 409
Rpta. : "C"
PREGUNTA 32:
En una serie de cuatro razones geométricas continuas iguales se cumple que la suma de las diferencia del primer y tercer antecedente , y el doble de la diferencia del segundo y el cuarto antecedente es 840. Hallar el máximo valor que puede tomar el primer consecuente si la constante de proporcionalidad es un número entero.
A) 189
B) 125
C) 280
D) 350
E) 120
Rpta. : "C"
PROBLEMAS RESUELTOS
PREGUNTA 1 :
En una caja hay 200 caramelos de dos sabores, limón y naranja , los cuales están en una relación de 3 a 1. ¿Cuál es la diferencia del número de caramelos que hay en la caja?
A) 50
B) 100
C) 150
D) 170
E) 180
RESOLUCIÓN :
# de caramelos de Limón : 3k
# de caramelos de Naranja : k
Según enunciado : 3k + k = 200
⇒ 4k = 200 ⇒ k = 50
Piden : 2k = 100
Rpta. : "B"
PREGUNTA 3 :
Si 45 es la cuarta diferencial de a, b y c; además, 140 es la tercera diferencial de 2a y 160. Halla la media aritmética de b y c.
A) 64,0
B) 66,0
C) 62,0
D) 63,5
E) 67,5
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 4 :
En una proporción geométrica continua, la suma y diferencia de los extremos exceden al término medio común en 49 y 31 unidades, respectivamente. Hallar la suma de los cuatro términos de dicha proporción.
A) 112
B) 125
C) 126
D) 121
E) 117
RESOLUCIÓN :
PREGUNTA 5 :
En una proporción geométrica de razón 5/4, la suma de los términos es 54. Si la diferencia de los consecuentes es 8, entonces el menor de los términos de la proporción es
A) 4
B) 5
C) 6
D) 7
E) 8
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 6 :
A un teatro asisten muchas personas, se sabe que de cada cinco varones que entran, tres entran con un niño y de cada siete mujeres, cuatro entran con un niño. Además, por cada seis varones entran cinco mujeres, si entraron 678 niños en total, ¿cuántos adultos entraron al teatro?
a) 1105
b) 1135
c) 1065
d) 1050
e) 1155
RESOLUCIÓN :
Rpta. : "E"
Un jugador de billar A le da ventaja a otro B, 40 carambolas para 100 y B le da ventaja a otro C, 60 carambolas para 100. ¿Cuántas carambolas de ventaja debe dar A a C en un juego de 100?
A) 64
B) 72
C) 76
D) 68
E) 74
RESOLUCIÓN :
Rpta. : "C"
CUARTA PRACTICA
PREGUNTA 1 :
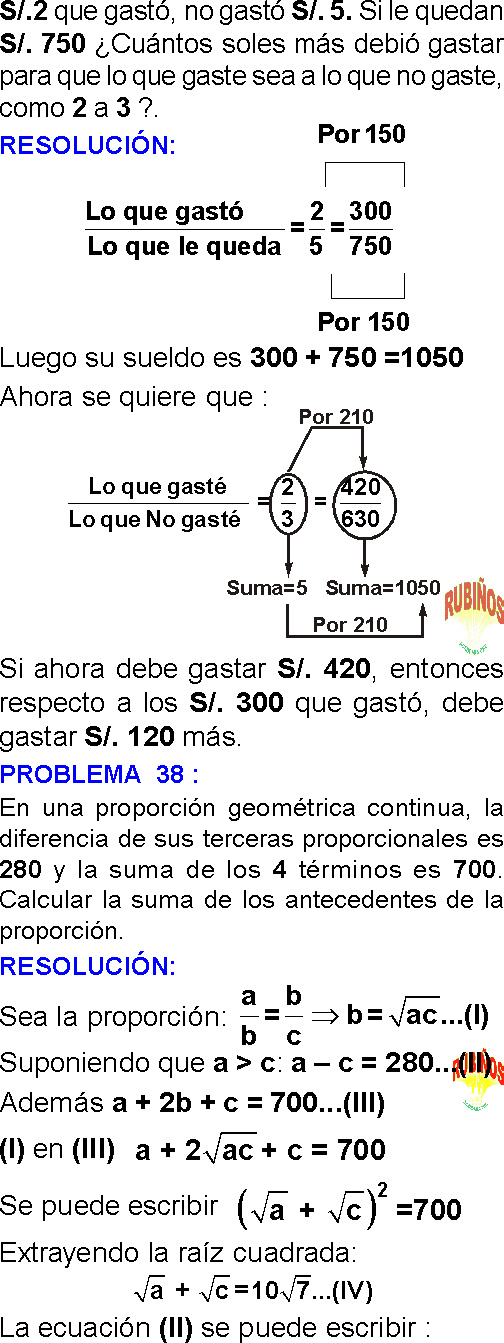
Lo que cobra y gasta un profesor suman 600. Lo que gasta y lo que cobra están en relación de 2 a 3. ¿En cuánto tiene que disminuir el gasto para que dicha relación sea de 3 a 5?
A) 16
B) 24
C) 32
D) 15
E) 20
PREGUNTA 2 :
El sueldo de Luis es al sueldo de Julio como 5 es a 3. Cierto mes por equivocación Julio recibió S/.720 más , con lo cual recibió la misma cantidad que Luis. ¿Cuánto es el sueldo de Luis?
A) S/. 1080
B) S/. 1200
C) S/. 1900
D) S/. 1700
E) S/. 1800
PREGUNTA 3 :
En una proporción geométrica la suma de los términos extremos es 20 y su diferencia 16. ¿Cuál es su media proporcional?
A) 9
B) 6
C) 3
D) 2
E) 7
PREGUNTA 4 :
La razón de dos números es 3/8 y su suma es 2 497. Encontrar el menor de los dos números.
A) 723
B) 681
C) 288
D)808
E) 729
PREGUNTA 5 :
A una fiesta concurren 360 personas , entre hombres y mujeres , asistiendo 5 hombres por cada 4 mujeres; después de 3 horas se retíran igual número de hombres y de mujeres ; quedan entonces 3 hombres por cada 2 mujeres. ¿Cuántas parejas formadas por un hombre y una mujer se retiraron?
A) 40
B) 80
C) 60
D) 30
E) 20
PREGUNTA 6 :
La edad de Pablo es a la edad de María como 9 es a 7. Si dentro de 5 años el doble de la edad de Pablo y el triple de la edad de María sumarían 103 años, determinar el valor de la razón aritmética de las edades actuales de Pablo y María.
A) 3 años
B) 4 años
C) 5 años
D) 6 años
E) 7 años
PREGUNTA 7 :
En una serie de 5 razones geométricas equivalentes continuas, el segundo antecedente es excedido en 70 por el cuarto consecuente. Determine la suma de los términos no extremos, si además se sabe que las razones suma 5/2.
A) 300
B) 315
C) 320
D) 340
E) 350
PREGUNTA 8 :
Si la media proporcional entra a y b es además 12 y la tercera proporcional entre a y b es 96, Determinar: (a² + b)
A) 60
B) 40
C) 80
D) 25
E) 90
PREGUNTA 9 :
En una proporción aritmética, los términos extremos son entre sí como 4 es a 3 y los términos medios son como 5 es a 9. Calcule la suma de antecedentes, si se diferencian en 18.
A) 306
B) 326
C) 126
D) 186
E) 94
PREGUNTA 10 :
En una proporción el producto de términos extremos es 30. Determinar la suma mínima de extremos, si la suma de medios es 17. Asuma que todos los términos de la proporción son enteros y diferentes.
A) 9
B) 10
C) 11
D) 12
E) 13
PREGUNTA 11 :
Si las razones aritméticas de los términos de la primera y segunda razón de una proporción son 8 y 24, respectivamente, determine en qué relación estarían la suma y la diferencia de los consecuentes de dicha proporción.
A) 9
B) 6
C) 3
D) 2
E) 7
PREGUNTA 12 :
Si el primer y último término de una proporción aritmética continua están en la relación de 5 a 1, además su media diferencial es igual a la cuarta proporcional de 6; 10 y 9, halle la suma de los términos diferentes de dicha proporción aritmética.
A) 40
B) 45
C) 50
D) 52
E) 60
PREGUNTA 13 :
En una granja, donde el número de pavos, patos y gallinas está en la relación de 13; 19 y 23, ocurre una epidemia cuya consecuencia fue la muerte de la quinta parte de los animales, Si los que murieron de cada especie son entre sí como 2; 11 y 9, respectivamente, determinar cual será la relación entre los que quedaron vivos.
A) 19 ; 20 y 23
B) 24 ; 27 y 37
C) 15 ;17 y 29
D) 15 ; 45 y 37
E) 37 ; 45 y 50
PREGUNTA 14 :
Si en una relación geométrica entre dos números cuya suma es 65, al menor se le suma 17 y al mayor se le resta 17 , la relación primitiva se invierte. ¿Cuál es el menor de dicho número?
A) 19
B) 18
C) 31
D) 23
E) 24
PREGUNTA 15 :
El radio de la Luna es los 3/11 del radio terrestre y el diámetro del Sol es igual a 108 diámetros terrestres. ¿Cuál es la razón geométrica entre los radios de la Luna y el Sol?
A) 2/37
B) 1/350
C) 2/367
D) 5/87
E) 1/396
PREGUNTA 16 :
Dos amigos parten simultáneamente al encuentro uno del otro con velocidades que están en relación de 7 a 5. Si cuando están a 168 m de distancia, antes del encuentro, duplican su velocidad; calcule qué distancia se alejó del punto de encuentro el más lento en el instante en que el otro cruza el punto en el cual ambos aumentaron sus velocidades.
A) 30 m
B) 40 m
C) 50 m
D) 60 m
E) 70 m
PREGUNTA 17 :
En una serie de razones geométricas iguales , los antecedentes son 2; 3; 7 y 11, mientras que el producto de los consecuentes es 37 422. ¿Cuál relación entre consecuente y antecedente?
A) 9
B) 6
C) 3
D) 2
E) 7
CLAVES – RESPUESTAS : 1)B 2)E 3)B 4)B 5)B 6)B 7)A 8)A 9)A 10)C 11)D 12)B 13)B 14)E 15)E 16)C 17)C
QUINTA PRACTICA
PREGUNTA 1 :
En la granja de Estela, la cantidad de conejos es a la cantidad de pavos como 5 a 3. Se vende la mitad de los conejos y 20 pavos, quedando así la nueva relación entre la cantidad de conejos y pavos de 5 a 4, ¿ cuántos animales se vendieron entre conejos y pavos?
A) 20
B) 50
C) 70
D) 90
PREGUNTA 2 :
Amy tiene 3 bolsas de caramelos de diferentes tipos, para repartir a un grupo de niños . Las cantidades de caramelos que tienen estas bolsas están en la en la relación de 4; 5 y 7 en ese orden. Si se desea que estas bolsas de caramelos contengan la misma cantidad, de una de las bolsas se debe sacar 30 caramelos, para distribuir en las otras dos. Calcule la cantidad de caramelos de la bolsa de mayor contenido.
A) 115
B) 120
C) 126
D) 210
PREGUNTA 3 :
Lenin es un trabajador del campo que percibe una remuneración mensual de (700 + 10a) soles ; para solventar emergencias medicas o de otro tipo Lenin ahorra de este salario S/.2 por cada S/.3 que gasta. ¿En cuánto debe disminuir sus gastos para que la relación entre lo que ahorra y gasta sea de 4 a 3?
A) S/150
B) S/120
C) S/90
D) S/240
PREGUNTA 4 :
En un colegio , por cada 5 varones adultos que entran, 3 de ellos entran con su niño; y por cada 7 mujeres adultas, 4 de ellas entran con su niño. Además, por cada 6 varones adultos, entran 5 mujeres adultas Si en total han entrado 678 niños, ¿cuántos varones adultos han entrado?
A) 630
B) 470
C) 550
D) 583
PREGUNTA 5 :
Aldo, Leo y Amy son funcionarios públicos, de sus remuneraciones mensuales se sabe que: lo que perciben Aldo y Leo están en la relación de 3 a 7, mientras que de Leo y Amy esta en la relación de 5 a 3. ¿Cuánto percibe mensualmente Leo sabiendo que si Amy le diera S/600 a Aldo , estos dos tendrían la misma cantidad?
A) S/1500
B) S/4500
C) S/3500
D) S/ 2100
PREGUNTA 6 :
Se diluye 50 L de alcohol en 30 L de agua, para mayor efectividad contra un virus y bacterias, se decide extraer 24 L de la mezcla y reemplazar por alcohol. Sin embargo, se decide que la mezcla final tenga por cada 3 L de agua 10 L de alcohol, para ello, ¿cuántos litros de alcohol se debe añadir?
A) 14
B) 19
C) 11
D) 21
PREGUNTA 7 :
Se tiene 3 bidones de agua casi llenos (A, B y C) donde el volumen de A es al de B como 6 es a 4 y el volumen de B es al de C como 12 es a 9. Si del bidón A se pasa m litros a B y luego de este se pasa n litros a C de manera que los volúmenes de los 3 bidones sean iguales, determine la relación en la que encuentran m y n.
A) 3 a 2
B) 5 a 4
C) 2 a 3
D) 5 a 3
PREGUNTA 8 :
Fiesta de promoción ¿recuerdas cuando estabas en el colegio? Todos esperan que sea un día inolvidable en sus vidas. El día del evento al inicio se observa que número de varones que están bailando es al número de mujeres que no bailan como 3 a 2, y la diferencia entre el número de mujeres que bailan y las que no bailan es al total de personas como 1 a 11. Si luego de una 1 hora llegan un cierto número de parejas, entonces la relación entre el número de varones y el numero de mujeres es como 9 a 8 La relación entre el número de mujeres al inicio del evento y al final es de
A) 5 a 8.
B) 4 a 5.
C) 3 a 7.
D) 2 a 5.
PREGUNTA 9 :
Un enólogo dispone de los clases de vino, antes del embotellado hace mezclas en 3 recipientes. En el primero en la razón de 2 a 1, en el segundo en la relación de 3 a 2 y en el tercer en la relación de 1 a 3. Para obtener un vino rico por naturaleza se extrae el mismo volumen de los tres recipientes para formar una mezcla que contenga 267 litros de vino de la segunda clase. ¿Cuántos litros de la primera clase se uso?
A) 210
B) 273
C) 240
D) 222
PREGUNTA 10 :
Con los pesos de 4 personas se puede formar una serie de 3 razones geométricas equivalentes continuas, la suma de los dos primeros consecuentes de la serie es a la suma de los dos últimos consecuentes como 3 es a 2. Si la suma de los dos primeros antecedentes de esta serie es 180, calcule la suma de los pesos de las 4 personas.
A) 360
B) 240
C) 260
D) 300
PREGUNTA 11 :
En el aniversario de bodas de oro del matrimonio Torres , se observa, que el número de varones y mujeres están en la relación de 3 a 7. La cantidad de personas que bailan y no lo hacen están en la relación de 2 a 3, respectivamente; de los varones solteros, los que bailan y no bailan son iguales y son a la vez el doble de los varones casados. Calcule cuántas mujeres no bailan si estas varían entre 200 y 250.
A) 240
B) 220
C) 225
D) 210
PREGUNTA 12 :
En una serie de cuatro razones geométricas equivalentes y continuas, el producto de dos de las razones cualesquiera es 4/9. Determine la suma de los términos de la última razón, si la razón aritmética del tercer consecuente y el tercer término es 90.
A) 135
B) 300
C) 405
D) 400
PREGUNTA 13 :
Se tiene cuatro recipientes de igual capacidad con volúmenes de alcohol los cuales están en la misma relación que los números 3; 4; 5 y 9. Se tiene aparte un cierto volumen de agua que reparte en cada uno de los cuatro recipientes iniciales hasta llenarlos. Si el volumen que se agrega al primero y segundo recipiente es de 26 litros, lo que se agrega al segundo y tercero suman 22 litros y finalmente se agrega 12 litros al tercero y cuarto. ¿Qué capacidad tenían los 4 recipientes iniciales?
A) 22
B) 20
C) 30
D) 25
PREGUNTA 14 :
Las edades de tres amigos (A, B y C) y las edades de sus respectivas novias (M, N y P) forma una serie de 3 razones geométricas equivalentes tal que la suma de dos de estas razones es 4/3. Si el producto de los dos primeros antecedentes de esta serie es 440 así mismo el producto de los dos últimos consecuentes es 1287, calcule la suma de las edades de la pareja más joven
A) 55
B) 65
C) 44
D) 50
PREGUNTA 15 :
En una serie de tres razones geométricas continuas, los cuadrados de las sumas de consecuentes y antecedentes están en la relación de 75 a 108, respectivamente, calcule la diferencia del primer y tercer consecuente si el tercer término es 720.
A) 220
B) 221
C) 200
D) 132
CLAVES – RESPUESTAS : 1)C 2)C 3)B 4)A 5)C 6)C 7)B 8)A 9)B 10)C 11)A 12)C 13)B 14)D 15)A
Magnitud es una propiedad que poseen todos los cuerpos, fenómenos y relaciones entre ellos, que permite que puedan ser medidos y dicha medida, representada en la cantidad, puede ser expresada mediante números sobre la base de una comparación con otro cuerpo o fenómeno que se toma como patrón.
La masa, el tiempo, la longitud, el volumen, la rapidez, la temperatura, entre muchas otras, son magnitudes. No debe confundirse magnitud con cantidad.
La magnitud es la propiedad, la cantidad es cuánto de eso tiene la magnitud.
Por ejemplo, el tiempo es una magnitud, pero 12 horas es una cantidad.
Toda medición consiste en atribuir un valor numérico cuantitativo a alguna propiedad de un cuerpo, como la longitud o el área.
Estas propiedades, conocidas bajo el nombre de magnitudes físicas, pueden cuantificarse por comparación con un patrón o con partes de un patrón.
Constituyen ejemplos de magnitudes físicas, la masa , la longitud , el tiempo , la densidad , la temperatura , la velocidad y la aceleración; caracterizadas por un valor fijo independiente del observador y carecen de dirección y sentido, como por ejemplo, la masa.
En física clásica la masa, la energía, la temperatura o la densidad de un cuerpo son magnitudes escalares ya que contienen un valor fijo para todos los observadores.
El término magnitud puede referirse a: la magnitud física, aquella propiedad de los sistemas físicos susceptible de ser medida; la magnitud matemática, una propiedad matemática relacionada con el tamaño. patrón de medida : Escala o medida previamente definido y aceptado en un determinado ámbito.
MEDIR : Decir cuántas veces se encuentra incluido el patrón de medida.
PATRON DE MEDIDA :
Escala o medida previamente definido y aceptado en un determinado ámbito.
MEDIR : Decir cuántas veces se encuentra incluido el patrón de medida.


























































































































.png)
.png)