UNI 2025-1 TERCERA PRUEBA CLAVES DE INGRESO UNIVERSIDAD DESARROLLO DE FÍSICA QUÍMICA PDF

PREGUNTA 1 :

Los vectores A y B tienen magnitudes de 4m y 5m respectivamente. Si su producto escalar es 12 m², determine la magnitud del producto vectorial (en m²) de estos vectores.

A) 10

B) 12

C) 20

D) 16

E) 25

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 2 :

Un insecto se posa en el borde de un disco de 100 cm de diámetro, que gira a razón de 5 revoluciones por cada 4s. Dadas las siguientes proposiciones:

I) La magnitud de la aceleración centrípeta del insecto es de 25𝛑²/9 m/s².

II) Si se mantiene la misma velocidad angular y si el diámetro del disco hubiera sido de 50 cm, la magnitud de la aceleración centrípeta del insecto sería 25𝛑²/16 m/s²..

III) La magnitud de la velocidad angular del insecto es 5𝛑 rad/s.

Son correctas:

A) solo II

B) I y III

C) solo III

D) solo I

E) I y II

RESOLUCIÓN :

MCU

Rpta. : "A"

PREGUNTA 3 :

En el extremo de una cuerda, sometida a una fuerza de tensión de magnitud 20N, se genera una onda que se propaga con una amplitud de 0,05 m y con una longitud de onda de 3,14 m. Calcule (en J/m) la energía por unidad de longitud que se transmite a lo largo de la cuerda.

Considere 𝛑=3,14.

A) 0,1

B) 0,2

C) 0,3

D) 0,4

E) 0,5

RESOLUCIÓN :

ONDAS MECÁNICAS

Rpta. : "A"

PREGUNTA 4 :

En la figura se muestra la masa M moviéndose con una rapidez de 2,7 m/s y las masas de 2M y 4M en reposo, de modo que todas las masas están sobre una superficie horizontal lisa. Si todas las colisiones son elásticas y unidimensionales, determine la rapidez (en m/s) de la masa 4M, luego de ser colisionada por la masa 2M.

A) 0,55

B) 0,80

C) 1,20

D) 1,80

E) 2,70

RESOLUCIÓN :

CANTIDAD DE MOVIMIENTO Y CHOQUES

Rpta. : "C"

PREGUNTA 5 :

Se tiene una esferita unida a una cuerda con uno de sus extremos sujeto al techo. Se suelta la esferita desde el punto A partiendo del reposo (ver figura). Cuando la cuerda llega a la línea vertical CV, la esferita se desprende de la cuerda en el punto B. Luego, la esferita viaja sola llegando a impactar en el punto D.

Considerando insignificante la masa de la cuerda y siendo VD=30cm, BV=25 cm, halle h (en cm).

A) 1

B) 9

C) 19

D) 25

E) 30

RESOLUCIÓN :

ENERGÍA MECÁNICA

Rpta. : "B"

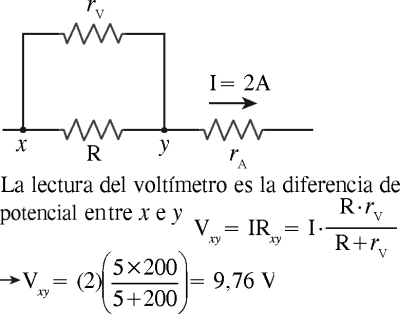
PREGUNTA 6 :

En el circuito mostrado, la diferencia de potencial entre A y B es 10,16V. Calcule aproximadamente (en V) la diferencia de potencial medida por el voltímetro si su resistencia interna es de 200Ω. Considere que la resistencia interna del amperímetro es diferente de cero y este registra 2 A de intensidad de corriente.

A) 10,76

B) 6,76

C) 8,76

D) 9,76

E) 7,76

RESOLUCIÓN :

ELECTRODINÁMICA

Rpta. : "D"

PREGUNTA 7 :

Un cable rectilíneo de 16cm de longitud, se encuentra en un campo magnético constante homogéneo de 7mT. Calcule (en A) la corriente eléctrica que fluye por el cable, si la fuerza máxima que experimenta el cable es de 0,021N.

A) 18,75

B) 28,75

C) 58,75

D) 48,75

E) 38,75

RESOLUCIÓN :

ELECTROMAGNETISMO

Rpta. : "A"

PREGUNTA 8 :

Dos cargas puntuales +Q y – Q/9 se encuentran fijas y separadas una distancia X, de tal forma que en un punto P a 3 cm de +Q, la intensidad del campo eléctrico es cero. Determine el valor de X (en cm).

A) 0,5

B) 1,0

C) 2,0

D) 2,5

E) 1,5

RESOLUCIÓN :

ELECTROSTÁTICA

Rpta. : "C"

QUÍMICA

PREGUNTA 1 :

Dadas las siguientes proposiciones indique la secuencia correcta después de determinar si la proposición es verdadera (V) o falsa (F).

I) El modelo atómico actual aún conserva la idea de J. Dalton al establecer que todos los átomos de un mismo elemento son idénticos.

II) El principal inconveniente en el modelo de N. Bohr fue que los electrones van perdiendo energía al girar en torno al núcleo y colapsarían sobre este en un tiempo muy corto.

III) El modelo atómico actual, basado en la mecánica cuántica, supone que los electrones tienen exclusivamente un comportamiento corpuscular, girando alrededor del núcleo en órbitas elípticas.

A) FFV

B) FFF

C) VVF

D) VVV

E) FVV

RESOLUCIÓN :

MODELOS ATÓMICOS

I. Falso

El modelo atómico actual considera a los isótopos (átomos del mismo elemento con masas diferentes).

John Daltón en uno de sus postulados señala que los átomos de un mismo elemento son idénticos en su composición y propiedades, sin embargo posteriormente se descubren que existen isótopos cuyos átomos difieren en algunas propiedades como por ejemplo su masa, volumen, densidad, esto para todo elemento químico.

II. Falso

El enunciado no corresponde al modelo de Bohr, sino al inconveniente en el modelo de Rutherford.

Es inconveniente (o inconsistencial de la estabilidad energética del electrón al orbitar al núcleo del átomo era del modelo atómico sistema planetario en miniatura (átomo nuclear) planteado por Ernest Rutherford en 1911, fue Niels Bohr quien en 1913 plantea en su modelo atómico cuántico la estabilidad del electrón suponiendo órbitas de energía estacionaria, en consecuencia el electrón en tanto se encuentre en cierta órbita no irradia, ni absorbe energía.

III. Falso

El modelo actual no plantea un giro en órbitas elípticas, sino en un orbital atómico (región del espacio en la que existe una gran probabilidad de encontrar uno o dos electrones).

El modelo atómico actual, basado en la mecánica cuántica, supone a los electrones con un comportamiento dual “Onda-partícula” al girar entorno al núcleo del átomo.

Rpta. : "B"

PREGUNTA 2 :

La borazina es también conocida como “benceno inorgánico”, debido a su semejanza estructural con el benceno. Indique su fórmula empírica, si presenta la siguiente composición porcentual en masa: 40,74% de boro (B); 51,85% de nitrógeno (N) y 7,41% de hidrógeno (H).

Masas atómicas: H=1; B=11; N=14

A) B₃NH₂

B) BN₃H₆

C) B₃NH

D) B₃N₂H₅

E) BNH₂

RESOLUCIÓN :

FÓRMULA EMPÍRICA

Rpta. : "E"

PREGUNTA 3 :

Con respecto a la lluvia ácida, indique la secuencia correcta después de determinar si la proposición es verdadera (V) o falsa (F).

I) Es producida por los gases de efecto invernadero.

II) El pH de dicha lluvia es mayor a 6,5.

III) Su acidez se debe principalmente a la presencia de CO₂.

A) FVV

B) FFV

C) FFF

D) VVV

E) VFV

RESOLUCIÓN :

CONTAMINACIÓN AMBIENTAL

I. Falso

La lluvia ácida contiene, principalmente, HNO₃ y H₂SO₄, que se originan de los óxidos gaseosos SO_x y NO_x.

II. Falso

Se considera lluvia ácida cuando el valor de pH es menor a 5,6.

III. Falso

La acidez de la lluvia ácida se debe a la presencia de iones H+ que provienen de la disociación total de H₂SO_4(ac) y HNO_3(ac).

Rpta. : "C"

PREGUNTA 4 :

Si a 10mL de una solución de KOH 0,22 mol/L se adiciona 100 mL de agua, calcule el pH a 25°C de la solución resultante.

Dato: log2=0,30

A) 2,30

B) 1,70

C) 11,70

D) 7,00

E) 12,30

RESOLUCIÓN :

SOLUCIONES (DILUCIÓN Y PH)

Rpta. : "E"

PREGUNTA 5 :

Dadas las proposiciones para los siguientes sistemas en equilibrio a una cierta temperatura: (1) 2NO_(g)+O_2(g)⇄ 2NO_2(g); K_p=K₁

(2) 2NO_2(g)⇄ N₂O_4(g); K_p=K₂

I) Para el sistema:

2NO_2(g) ⇄ 2NO_(g)+O_2(g),

el valor de la constante de equilibrio es K_p=1/K₁.

II) Si se multiplica por 2 la ecuación (2), el valor de la constante de equilibrio es K_p=2K₂.

III) La constante de equilibrio para el sistema:

2NO_(g)+O_2(g) ⇄ N₂O_4(g) es K_p=K₁×K₂.

A) I, II y III

B) I y III

C) solo I

D) solo III

E) solo II

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 6 :

Señale los pares de compuestos que son solubles:

I) NaCℓ_(s) con H₂O₍_ℓ₎ a 20 ºC

II) CH₃OH₍_ℓ₎ con C₂H₅OH₍_ℓ₎ a 25 ºC

III) H₂O₍_ℓ₎ con CCℓ₄₍_ℓ₎ a 20 ºC

A) I, II y III

B) I y II

C) solo II

D) II y III

E) solo I

RESOLUCIÓN :

SOLUCIONES

Piden identificar los compuestos que son solubles (mezcla homogénea). Para ello, los compuestos deben tener la misma naturaleza, y cumplirá que lo semejante disuelve a su semejante.