SIMULACRO UNPRG 2025 UNIVERSIDAD PEDRO RUIZ RESUELTO CLAVES PDF
TEXTO
Galileo es famoso , con todo derecho , por defender la idea de que la Tierra gira alrededor del sol , en contra de las autoridades religiosas que no consideraban convenientemente esta idea. Fue el primer mártir de la ciencia , a pesar de que abandonó públicamente sus ideas, sometido por la Inquisición. Pero Galileo no inventó la teoría heliocéntrica , sino Nicolás Copérnico , que posteriormente fue perfeccionada por Kepler. No obstante , la verdadera grandeza de Galileo radica en que él implantó el método experimental ; del que la ciencia moderna depende.
PREGUNTA 1 :
De acuerdo con el texto
A) Galileo fue el primero en sostener la teoría heliocéntrica.
B) la religión siempre ha rechazado a la ciencia.
C) Galileo no debió renunciar a su teoría.
D) Copérnico fue superior que Galileo.
E) Galileo desarrolló el método experimental.
RESOLUCIÓN :
El texto nos informan claramente sobre Galileo y las contrariedades que tuvo , y el nexo adversativo (no obstante) encabeza la idea central del texto: Galileo formuló el método experimental , mas no la teoría heliocéntrica , es la verdadera contribución de este científico italiano. Por lo tanto se concluye del texto , que Galileo desarrolló el método experimental.
Rpta. : "E"
PREGUNTA 2 :
Indique la alternativa que completa adecuadamente el significado de la siguiente oración. ¿Cómo podré _____________ a los demás si no tengo el ________ de mi mismo?
A) educar – alumno y paciencia
B) complacer – espíritu burlón
C) convencer – don y la palabra
D) elegir – elector y los votos
E) gobernar – dominio y control
RESOLUCIÓN :
‘‘¿Cómo podré gobernar a los demás si no tengo el dominio y control de mi mismo? ’’
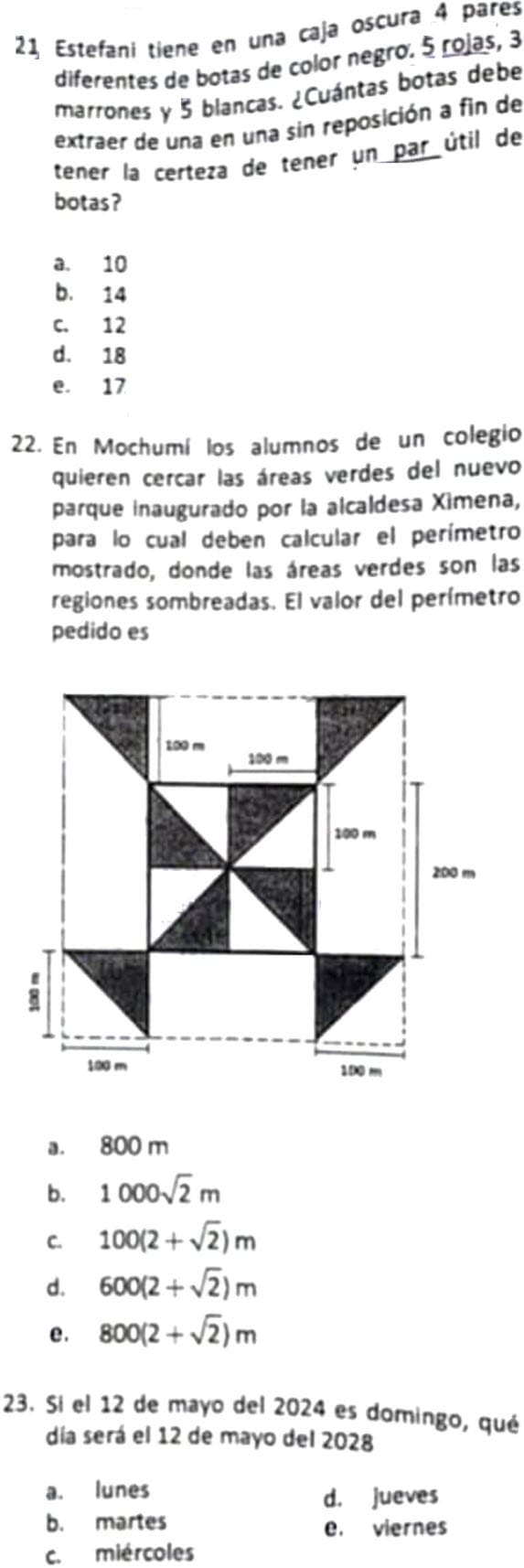
La oración planteada como interrogante , hace ver que si la persona no puede hacer algo consigo misma, no podrá hacerlo con los demás.
Rpta. : "E"
PREGUNTA 3 :
Lea los enunciados y elija la alternativa que establece la secuencia correcta de las oraciones según el título.
Motores y Centrales Hidroeléctricas
I) Las plantas de energía hidroeléctrica requieren diferentes turbinas con funciones y potencias específicas.
II) La turbina Pelton , por último , solo puede usarse en las usinas de alta presión en las que el agua desciende más de 200 metros.
III) La turbina Kaplan , por ejemplo , se usa cuando el agua desciende a menos de 150 metros.
IV) La energía de la caída del agua se usa en las plantas hidroeléctricas para generar electricidad.
V) La turbina Francis , en cambio , se usa en las usinas donde el agua desciende entre 150 a 200 metros.
A) IV, I, III, V, II
B) III, I, IV, V, II
C) I, IV, III, II, V
D) IV, I, II, V, III
E) I, III, V, IV, II
RESOLUCIÓN :
El esquema lógico sobre MOTORES y CENTRALES HIDROELÉCTRICAS debe seguir un orden de generalidad :
Concepto de central hidroeléctrica: (IV) La energía de la caída del agua se usa en las plantas hidroeléctricas para generar electricidad. Idea de motor: (I) Las plantas de energía hidroeléctrica requieren diferentes turbinas con funciones y potencias específicas. Función de los motores : (III) La turbina Kaplan, por ejemplo , se usa cuando el agua desciende a menos de 150 metros. Función de los motores: (V) La turbina Francis , en cambio, se usa en las usinas donde el agua desciende entre 150 a 200 metros. Función de los motores: (II) La turbina Pelton , por último , solo puede usarse en las usinas de alta presión en las que el agua desciende más de 200 metros.
Por lo tanto , la secuencia correcta: IV , I , III , V , II
Rpta. : "A"
PREGUNTA 4 :
Marque la alternativa que , al insertarse en los espacios en blanco del enunciado , dé un significado correcto.
Cuando el uso de la fuerza se hace necesario e inevitable, la civilización exige que ,______ ante el triunfo, se muestre ponderación y decoro ; y , _________, frente a la derrota, resignación y esperanza.
A) por un lado - por otro lado
B) primero - después
C) mientras - luego
D) por ejemplo - por eso
E) si bien - también
RESOLUCIÓN :
Cuando el uso de la fuerza se hace necesario e inevitable, la civilización exige que, por un lado ante el triunfo, se muestre ponderación y decoro; y ,
por otro lado, frente a la derrota, resignación y esperanza.
Los conectores que completan son:
por un lado : nexos distributivos una frente al triunfo
por otro lado : nexos distributivos la otra ante la derrota
Rpta. : "A"
PREGUNTA 5 :
Elija la oración que no tiene relación directa con el tema central del texto.
(I) El 31 de octubre se encontró una gran cantidad de lingotes de oro y plata en Nueva York. (II) Este hallazgo fue entre los escombros de las Torres Gemelas. (III) La elaboración de los lingotes de oro necesita pasar por un proceso de refinación muy laborioso. (IV) Un barco canadiense había informado que en sus oficinas en las Torres Gemelas , tenía lingotes por más de 200 millones de dólares. (V) Los lingotes fueron trasladados a un lugar seguro.
A) I
B) II
C) III
D) IV
E) V
RESOLUCIÓN :
El tema central del texto es el hallazgo de los lingotes de oro y plata en la ciudad de Nueva York (I) encontradas en un determinado lugar (lI) que tenían un dueño (IV) y fueron guardados en lugar seguro (V). La oración (III) encierra la idea de fabricación de los lingotes , que no guarda coherencia con las demás.
La elaboración de los lingotes de oro necesita pasar por un proceso de refinación muy laborioso.
Rpta. : "C"
PREGUNTA 6 :
Se reúnen 4 estudiantes de la U , cada uno de ellos de distinta especialidad: medicina, derecho, farmacia y odontología; cada uno de ellos procede de diferente departamento: Ica, Tumbes, Amazonas y Puno, no necesariamente en ese orden; y para refrescarse, prefieren bebidas diferentes: té, café, leche y jugo, no necesariamente en ese orden. Si se sabe que Julio toma té; el de Ica estudia odontología; Carlos no estudia medicina; el que prefiere jugo es de Tumbes; Gustavo es de Amazonas; el que toma leche estudia derecho; Enrique no es de Tumbes y el de Puno toma café.
¿Qué estudia Carlos y de qué departamento es Enrique?
A) Derecho – Ica
B) Farmacia – Tumbes
C) Odontología – Amazonas
D) Medicina –Tumbes
E) Farmacia – Puno
Rpta. : "E"
PREGUNTA 7 :
Ana, Alicia, Abiel, Alexandra, Almendra y Anais se ubican alrededor de una mesa circular en seis asientos distribuidos simétricamente, como se muestra en la figura.
Además, se sabe lo siguiente:
• Anais no está sentada al lado de Alicia ni de Almendra.
• Alicia no está sentada al lado de Ana ni de Abiel.
• Abiel no está sentado al lado de Ana ni de Almendra.
• Alexandra está sentada junto y a la derecha de Alicia.
¿Quién está sentado junto y a la izquierda de la persona que está sentada junto y a la izquierda de Ana?
A) Alicia
B) Anais
C) Almendra
D) Alexandra
E) Abiel
Rpta. : "E"
PREGUNTA 8 :
Ricardo, Saúl y Tomás llegaron a la final del Concurso Nacional de Matemática y rinden tres exámenes: Álgebra, Trigonometría y Lógico-Matemática. En cada prueba, el que queda primero recibe «a» puntos, el segundo recibe «b» puntos y el tercero «c» puntos, donde a; b y c son números enteros positivos tales que a>b>c. No hay empates, y en total, Ricardo acumuló 20 puntos; Saúl, 10 puntos y Tomás, 9 puntos. Sabiendo que Ricardo quedó segundo en el examen de Lógico Matemática.
¿Quién quedó tercero en el examen de Álgebra y quién, segundo en Trigonometría?
A) Tomas y Ricardo
B) Saúl y Tomás
C) Ricardo y Saúl
D) Tomás y Tomás
E) Ricardo y Ricardo
Rpta. : "B"