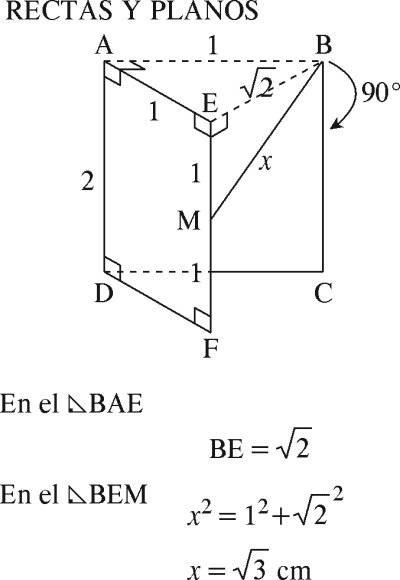
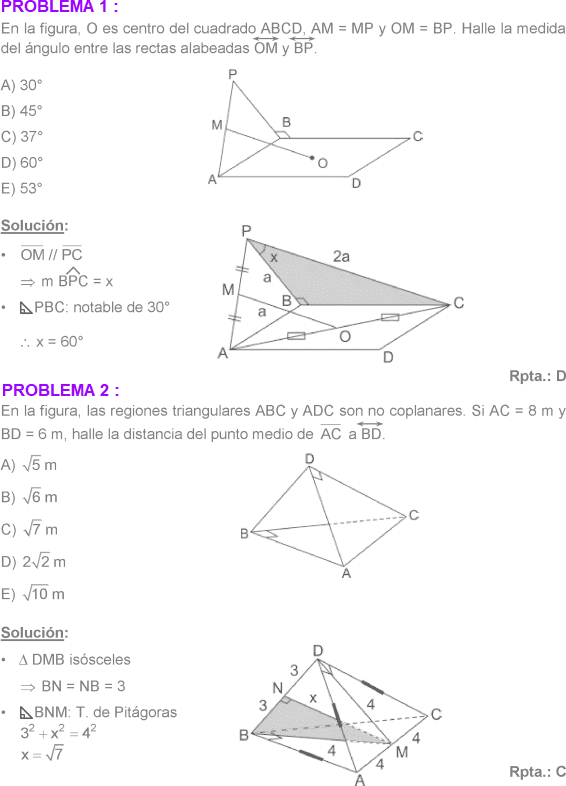
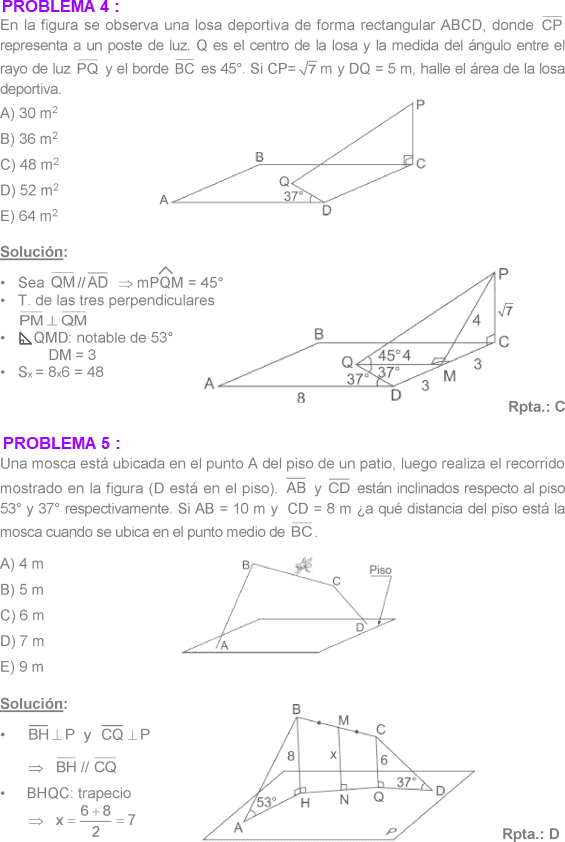
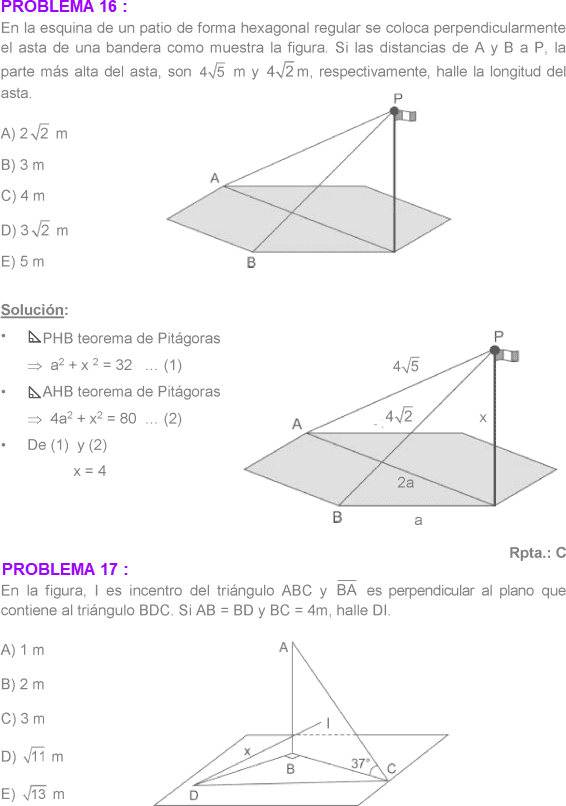
RECTAS Y PLANOS EN EL ESPACIO EJERCICIOS RESUELTOS PDF TEOREMA DE LAS TRES PERPENDICULARES

APRENDIZAJES ESPERADOS

• Diferenciar las distintas posiciones que pueden adoptar las rectas y planos en el espacio geométrico.

• Reconocer los diferentes teoremas que se desprenden a partir de una recta perpendicular al plano.

• Conocer que es la proyección ortogonal, así como la medida del ángulo entre recta y plano

• Conocer y aplicar el teorema de las tres perpendiculares.

• Ver como el tema se aplica en nuestra vida cotidiana.

• Relacionar la habilidad obtenida en la geometría plana para resolver problemas de geometría del espacio.

• Emplear lo aprendido en la resolución de problemas tipo exámenes de admisión.

El hombre antiguo se dio cuenta que ciertas partes de la superficies de la Tierra, como la superficie de lagos y mares tenían ciertas características similares que más adelante darían origen al plano.

Asimismo observó el rastro que deja el paso de un cometa, la trayectoria de un río, etc. Todo ello le dio la idea de líneas rectas , líneas curvas, etc.

Se puede decir, entonces, que en la antigüedad se desarrolló la capacidad del descubrimiento a partir de la observación .

EL PLANO

El plano ℙ será una superficie ilimitada que comúnmente se dibuja con forma de paralelogramo.

LA RECTA

Asimismo la observación de la naturaleza nos da la idea de recta ℒ.

POSICIONES ENTRE DOS PLANOS PLANOS PARALELOS

Dos planos son paralelos, si ellos no tienen puntos de intersección, de ellos podemos afirmar que representan una misma dirección.

PLANOS SECANTES

Dos planos secantes son aquellos que tienen puntos de intersección. Dichos puntos forman una recta, la cual se denomina arista.

POSICIONES ENTRE RECTA Y PLANO RECTA CONTENIDA EN EL PLANO

Es aquella recta que tiene todos sus puntos en el plano.

RECTA SECANTE AL PLANO

Es aquella recta que tiene solo un punto en común con el plano.

RECTA PARALELA AL PLANO

Es aquella recta que no tiene punto en común con el plano.

POSICIONES ENTRE RECTAS RECTAS PARALELAS

No se cortan y tienen una misma dirección.

RECTAS SECANTES

Tienen un punto de corte o intersección.

RECTAS ALABEADAS

No se cortan y no tienen la misma dirección.

ÁNGULO ENTRE RECTAS ALABEADAS

La medida del ángulo entre dos rectas alabeadas se define como la medida angular que forma una de ellas con la recta paralela a la otra, convenientemente trazada.

RECTA PERPENDICULAR A UN PLANO

Para afirmar que una recta sea perpendicular a un plano, dicha recta debe formar 90° con dos rectas del plano que pasen por su pie.

TEOREMA

Si una recta es perpendicular a un plano, entonces será perpendicular a otras rectas contenidas en dicho plano.

PROYECCIÓN ORTOGONAL

Es aquella que se crea a partir del trazado de la totalidad de las rectas proyectantes perpendiculares a un cierto plano.

ÁNGULO ENTRE RECTA Y PLANO

Es aquel ángulo que forma la recta con su proyección ortogonal sobre el plano.

PRACTICA

EJERCICIO 1 :

Desde un punto exterior a una recta, ¿cuántas perpendiculares se pueden trazar a dicha recta?

a) 1

b) 2

c) 3

d) infinitos

e) 5

EJERCICIO 2 :

Averiguar el máximo número de planos que determinan siete puntos en el espacio.

a) 7

b) 21

c) 28

d) 14

e) 35

EJERCICIO 3 :

Calcular el máximo número de planos que se pueden formar con cuatro rectas paralelas.

a) 2

b) 4

c) 6

d) 8

e) 10

EJERCICIO 4 :

Señale verdadero (V) o falso (F), a las siguientes proposiciones:

• Dos rectas paralelas son coplanares.

• Tres puntos cualesquiera determinan un plano.

• La intersección de dos planos es una recta.

a) VVV

b) VFV

c) FFF

d) FVV

e) FFV

EJERCICIO 5 :

Cuántos planos determinan diez puntos y seis paralelas?

a) 130

b) 190

c) 195

d) 170

e) 200

EJERCICIO 6 :

Calcular el máximo número de planos que se pueden determinar con 12 puntos diferentes y no colineales.

a) 90

b) 220

c) 270

d) 360

e) 110

EJERCICIO 7 :

Decir si es verdadero (V) o falso (F):

• Si dos planos son paralelos a la misma recta, entonces dichos planos son paralelos entre sí.

• Dadas dos rectas que se cruzan, entonces siempre existe una recta perpendicular entre ambas.

• Todos los planos paralelos a un plano son paralelos entre sí.

• La intersección de tres planos es necesariamente una recta.

a) VVVF

b) FFFV

c) FVVF

d) FFVV

e) FVFV

EJERCICIO 8 :

Con "n" rectas paralelas y seis puntos en el espacio se han determinado como máximo 125 planos. Hallar "n".

a) 8

b) 10

c) 11

d) 12

e) 15

EJERCICIO 9 :

Se tiene un segmento AB, la diferencia de las distancias de “A” y “B” a un plano exterior es 7 u. Si la proyección de AB sobre el plano es igual a 24 u, hallar “AB”.

a) 26 u

b) 30

c) 28

d) 25

e) 32

EJERCICIO 10 :

Por un punto “P” interior del plano triangular ABC, se levanta la perpendicular PQ de modo que “Q” equidista de “A”, “B“ y “C”. Calcular qué punto notable es “P” para el triángulo ABC.

A) baricentro

B) incentro

C) ortocentro

D) circuncentro

E) ninguno en especial

EJERCICIO 11 :

Señalar verdadero (V) o falso (F):

• Dos rectas perpendiculares necesariamente son secantes.

• Dos rectas perpendiculares a un plano son perpendiculares entre sí.

• Si una recta es perpendicular a un plano entonces es perpendicular a todas las rectas contenidas en el plano.

a) VFV

b) FVV

c) FVF

d) VVF

e) FFV

EJERCICIO 12 :

Se tiene una circunferencia de diámetro AB igual a 10m. Por el punto “A” se levanta una perpendicular AD al plano de la circunferencia tal que AD = 6 m y en la circunferencia se traza la cuerda BC = 6 m. Calcular el área del triángulo DBC.

a) 28 m²

b) 15

c) 30

d) 60

e) 35

SEGUNDA PRACTICA

PREGUNTA 1 :

Indique verdadero (V) o falso (F) según corresponda.

I. Si dos rectas no se cortan entonces son paralelas.

II. Una recta se encuentra contenida en un plano cuando todos sus puntos se encuentran en dicho plano.

III. Si una recta no es secante a un plano es porque debe ser paralela a dicho plano.

A) FVF

B) FFF

C) VFV

D) FVV

Rpta. : "A"

PREGUNTA 2 :

Exteriormente a un cuadrado de centro O se ubica el punto Q, tal que AO=OQ, en CD se ubica el punto P. Si PC= 3(PD) = 3, calcule PQ. m∢POQ= 90°.

A) √13

B) 3

C) √17

D) 4

Rpta. : "A"

PREGUNTA 3 :

Dos puntos A y B situados a uno y otro lado de un plano ℙ distan 2 u y 10 u de dicho plano y la proyección de AB sobre el plano P mide 5 u. Halle AB.

A) 11 u

B) 12 u

C) 13 u

D) 14 u

Rpta. : "C"

PREGUNTA 4 :

En un plano ℍ se ubican los puntos A y B. P es un punto exterior a dicho plano, si la medida del ángulo que forma PA y PB con el plano ℍ es el 45° y 30° respectivamente. Además AP y PB son perpendiculares, calcule AB, si AP =2√2.

A) 2√5

B) 3√6

C) 2√6

D) 4√2

Rpta. : "C"

PREGUNTA 5 :

Se tiene un segmento AB, la diferencia de las distancia de A y B a un plano exterior es 7. Si la proyección de AB sobre el plano es igual a 24. Hallar AB.

A) 26

B) 24

C) 25

D) 30

Rpta. : "C"

PREGUNTA 6 :

La distancia de un punto P a un plano es 5, se traza PQ (Q pertenece al plano), de tal manera que la proyección de PQ sobre el plano es de 12. Halle PQ.

A) 7

B) 13

C) 18

D) 17

Rpta. : "B"

PREGUNTA 7 :

Sean ℙ y ℚ dos planos paralelos, A y B son dos puntos en los planos ℙ y ℚ respectivamente. Si la distancia entre los planos es 40 cm y la proyección del segmento AB en el plano ℚ tiene una longitud de 30 cm, halle AB.

A) 45 cm

B) 50 cm

C) 55 cm

D) 60 cm

Rpta. : "B"

PREGUNTA 8 :

Indique la secuencia correcta de verdad (V) o falsedad (F) respecto a las siguientes proposiciones.

I. Tres puntos determinan un plano.

II. Una recta y un punto determinan un plano.

III. Dos rectas determinan un plano.

A) VVV

B) VVF

C) FFF

D) FVF

E) VFV

Rpta. : "C"

PREGUNTA 9 :

Indique la secuencia correcta de verdad (V) o falsedad (F) respecto a las siguientes proposiciones:

I. La intersección de dos planos secantes es un segmento.

II. La intersección de tres planos puede ser un punto.

III. El plano divide al espacio en dos semiespacios.

A) VFV

B) FVV

C) FFV

D) VVV

E) VVF

Rpta. : "B"

PREGUNTA 10 :

Indique la secuencia correcta de verdad (V) o falsedad (F) con relación a las siguientes proposiciones.

I. Si dos planos no son secantes, entonces son paralelos.

II. Si dos rectas no son paralelas, entonces son alabeadas.

III. Dos rectas alabeadas están contenidas en el mismo plano.

A) FVV

B) FVF

C) VFV

D) FFV

E) VFF

Rpta. : "E"

PREGUNTA 11 :

Indique la secuencia correcta de verdad (V) o falsedad (F) respecto a las siguientes proposiciones. I. Por un punto se pueden trazar solo 3 rectas.

II. Por una recta pasan infinitos planos.

III. Dos puntos determinan una recta.

A) FVV

B) FVF

C) FFV

D) VFV

E) VVV

Rpta. : "A"

PREGUNTA 12 :

En un cuadrado ABCD se ubican los puntos medios M y N de los lados BC y AD; por M se traza un segmento MS no coplanar al cuadrado y por N se traza NQ paralela a MS, tal que Q y S en el mismo semiespacio, NQ= 5, MS= 4, AB= 3. Calcule al área de la región MNQS. (m∢QNM= 90°)

A) 15,5

B) 16,5

C) 17,5

D) 23,5

E) 13,5

Rpta. : "E"

PREGUNTA 13 :

Calcule la cantidad máxima de planos que se pueden determinar con 7 puntos.

A) 24

B) 28

C) 32

D) 35

E) 30

Rpta. : "D"

PREGUNTA 14 :

Indique la secuencia correcta después de determinar si la proposición es verdadera (V) o falsa (F).

I. Si dos planos son perpendiculares a dos rectas diferentes que se intersecan, entonces dichos planos también se intersecan.

II. El lugar geométrico que determinan los pies de los segmentos oblicuos de longitudes iguales trazadas desde un punto exterior a un plano es una circunferencia.

III. Toda recta es perpendicular a un plano, si es ortogonal a dos rectas diferentes no paralelas contenidas en dicho plano.

A) FFV

B) VVV

C) FFF

D) VVF

E) VFV

Rpta. : "B"

PREGUNTA 15 :

Por el circuncentro O de un triángulo equilátero ABC de lado a se traza la secta secante OP a su plano. Calcule la medida del ángulo AOP si AP=CP=BP.

A) 30°

B) 45°

C) 60°

D) 90°

E) 53°

Rpta. : "D"

PREGUNTA 16 :

Un segmento está comprendido entre dos planos paralelos cuya distancia es 15. Si la longitud del segmento es 17, halle la longitud de la proyección ortogonal del segmento sobre uno de los planos.

A) 2

B) 4

C) 5

D) 8

E) 16

Rpta. : "D"

PREGUNTA 17 :

Por los vértices de un cuadrado ABCD se levantan perpendiculares AP, BQ, CR y DS al plano que lo contiene y hacia un mismo semiespacio, de 6; 4; 10 y x unidades de longitud, respectivamente. Calcule x si PQRS es un paralelogramo.

A) 10

B) 11

C) 12

D) 13

E) 14

PREGUNTA 18 :

En el espacio, se tienen 6 rectas paralelas entre sí. Calcule la cantidad de planos que estas rectas determinan.

A) 10

B) 11

C) 12

D) 13

E) 15

PREGUNTA 19 :

Se tienen los cuadrados ABCD y ADEF ubicados en planos perpendiculares. Sea M el punto medio de EF. Halle la medida del ángulo formado por AE y BM.

A) 37°

B) 45°

C) 53°

D) 30°

E) 60°

PREGUNTA 20 :

Indique la secuencia correcta de verdad (V) o falsedad (F) respecto a las siguientes proposiciones.

I. Si dos rectas forman ángulos iguales con el mismo plano, dichas rectas son paralelas.

II. Si una recta es perpendicular a dos rectas contenidas en un plano, dicha recta es perpendicular al plano.

III. Si una recta es perpendicular a un plano, entonces es perpendicular a cualquier recta contenida en el plano.

A) FFV

B) VVV

C) FFF

D) VVF

E) VFV

PROBLEMAS RESUELTOS

PREGUNTA 1 :

Hallar el radio de la circunferencia de centro O, si AB es perpendicular al plano ℙ.

AF=12; BO=17; BA=9

A) 7

B) 17

C) 4

D) 8

E) 6

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 2 :

En la figuras, el triángulo rectángulo ABC está contenido en el plano H, m∢ACB=53°/2 y AB=2cm, D es un punto que no pertenece al plano H y DB es perpendicular al plano H, tal que DB=2cm. Halle el área de la región triangular ADC.

A) 2 cm²

B) 3 cm²

C) 6 cm²

D) 30 cm²

E) 8 cm²

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 3 :

En la figura se muestra la vista frontal de una puerta ADFE de dimensiones AD=2cm, AE=1 cm y EF=2ME. Halle la medida de la cuerda tensada MB, tal que la puerta gire 90°.