TRINOMIO CUADRADO PERFECTO EJERCICIOS RESUELTOS DE FACTORIZACIÓN PDF
¿QUÉ ES UN TRINOMIO CUADRADO PERFECTO ?
Un trinomio cuadrado perfecto es aquel polinomio de tres términos que tiene raíz cuadrada exacta, que se caracteriza porque sus términos extremos son cuadrados perfectos, y el término central es igual al doble de las raíces cuadradas de dichos términos extremos.
A² +2AB + B²= (A + B)²
A² – 2AB + B²= (A – B)²
Un trinomio es «cuadrado perfecto» cuando es el cuadrado de un binomio.
Un trinomio ordenado con relación a una variable es cuadrado perfecto cuando el primer y tercer término son cuadrados perfectos(o tienen raíz cuadrada exacta) y positivos, y el segundo término es el doble producto de sus raíces cuadradas .
A² ± 2AB + B²= (A ± B)²
El trinomio cuadrado perfecto es el desarrollo de un binomio al cuadrado, se caracteriza porque el doble del producto de la raíz de dos de sus términos es igual al tercer término.
Todo trinomio cuadrado perfecto se transforma en binomio al cuadrado.
PRACTICA DE CLASE
Factoriza los siguientes trinomios cuadrados perfectos:
EJERCICIO 1 :
z² + 8z + 16
EJERCICIO 2 :
x² – 18x + 81 =
EJERCICIO 3 :
x² + 30x + 225 =
EJERCICIO 4 :
49x²+9+42x =
EJERCICIO 5 :
x² – 24x + 144 =
EJERCICIO 6 :
4x² + 12x + 9 =
EJERCICIO 7 :
121x²+132x+36 =
EJERCICIO 8 :
x²+ 20x + 100 =
EJERCICIO 9 :
4a²+12a + 9
EJERCICIO 10 :
25x² – 10x + 1
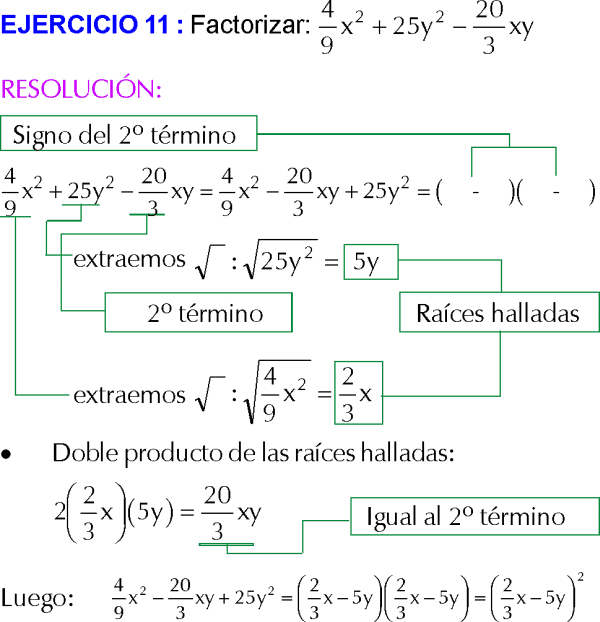
EJERCICIO 11 :
x² + 2x + 1
EJERCICIO 12 :
4x²+ 12xy + 9y²=
EJERCICIO 13 :
16a²+ 40a + 25 =
EJERCICIO 14 :
9x²+ 30x + 25 =
EJERCICIO 15 :
x4n – 18x2n + 81 =
EJERCICIO 16 :
4x² –28xy + 49y² =
EJERCICIO 17 :
a² – 10a + 25 =
EJERCICIO 18 :
x⁴ – 12x² + 36 =
EJERCICIO 19 :
1 – 8y + 16y² =
EJERCICIO 20 :
x⁴ – 10x² + 25 =
EJERCICIO 21 :
x2n+ 12xn + 36 =
EJERCICIO 22 :
49 + a² – 14a =
EJERCICIO 23 :
– 8z + 1 + 16z²=
FACTORIZACIÓN DE UN TRINOMIO CUADRADO PERFECTO
Cuando un trinomio (tres términos) después de haberlo ordenado, el primer y el tercer término son cuadrados perfectos y el segundo término es el doble producto de las bases de dichos términos, entonces se llama “Trinomio Cuadrado Perfecto”.
Todo trinomio cuadrado perfecto se descompone en dos factores binomios, que se obtienen extrayendo la raíz cuadrada de los términos primero y tercero, empleando el signo del segundo término.