ÁREAS DE REGIONES CIRCULARES EJERCICIOS RESUELTOS PDF
APRENDIZAJES ESPERADOS
• Conocer las fórmulas para calcular el área del círculo y de sus partes notables.
• Conocer la relación de áreas relativa a una región cuadrantal.
• Aplicar lo aprendido en la resolución de problemas sobre área del circulo y de sus partes notables.
La necesidad de calcular las áreas de diferentes superficies es la misma que motivó al cálculo del área de la región circular, aunque este reto no sería completamente resuelto hasta la llegada de Arquímedes. Con el cálculo del área de la región circular se involucraría aquel número misterioso conocido como PI.
REGIÓN CIRCULAR
El área de un círculo es igual al producto de Pi por el cuadrado del radio de la circunferencia que lo limita.
CÍRCULO :
Es el conjunto de puntos de la circunferencia y de su interior.
De otra manera, un círculo o una región circular es la reunión de una circunferencia y su interior.
Cuando hablamos del "área del círculo", queremos decir el área de la región circular correspondiente. (Este es el mismo modo de abreviar que se utiliza cuando hablamos del "área de un triángulo", queriendo decir el área de la región triangular correspondiente).
ÁREA DE UN CÍRCULO :
El área de un círculo es igual a multiplicado por el cuadrado del radio.
ÁREA DE UN SECTOR CIRCULAR :
Es aquella porción de círculo limitados por un ángulo central y su arco correspondiente.
El área de un sector circular es igual al semiproducto de la longitud del arco correspondiente al sector por la longitud de su radio.
ÁREA DE UNA CORONA CIRCULAR :
Es una parte de un círculo comprendido entre dos circunferencias concéntricas.
El área de la corona circular es el resultado de restarle al área de la circunferencia mayor el área de la circunferencia menor.
ÁREA DE UN TRAPECIO CIRCULAR :
Un trapecio circular es la parte de una corona circular comprendida entre dos radios del círculo mayor.
El área del trapecio circular es el resultado de restarle al sector circular mayor el sector circular menor.
GUIA DE CLASE BÁSICA
EJERCICIO 1 :
Calcular el área del círculo. Si la longitud de su radio mide 16√3
a) 120𝛑 cm²
b) 108𝛑
c) 124𝛑
d) 72𝛑
e) 180𝛑
Rpta. : "B"
EJERCICIO 2 :
Calcular el área de un círculo inscrito en un cuadrado de perímetro 16 cm.
a) 12𝛑 cm²
b) 18𝛑
c) 4𝛑
d) 16𝛑
e) 8𝛑
Rpta. : "C"
EJERCICIO 3 :
Calcular el área de un círculo inscrito en un sector circular de 60° y radio 6.
a) 12𝛑
b) 18𝛑
c) 4𝛑
d) 6𝛑
e) 8𝛑
Rpta. : "C"
EJERCICIO 4 :
Si el área de un círculo es 36𝛑 cm² , hallar el área del cuadrado inscrito en la circunferencia de dicho círculo.
a) 72 cm²
b) 48𝛑
c) 64𝛑
d) 96𝛑
e) 90𝛑
Rpta. : "A"
ÁREA DE UN SEGMENTO CIRCULAR :
Es una porción del círculo comprendido entre una cuerda y el arco correspondiente.
El área del segmento circular es igual al área del sector circular menos el área del triángulo que forman los puntos del sector circular.
ZONA O FAJA CIRCULAR :
Es una porción del círculo comprendido entre dos cuerdas paralelas.
LÚNULA :
Es una región plana no convexa limitada por dos arcos de circunferencia secante.
PROPIEDADES
I) En todo triángulo rectángulo se cumple que la suma de las áreas de las figuras semejantes construidas sobre los catetos es igual al área de la figura semejante construida sobre la hipotenusa.
II) LÚNULAS DE HIPÓCRATES :
Si en un triángulo rectángulo sobre sus lados se construyen exteriormente semicircunferencias, se cumple que la suma de las áreas de las lúnulas formadas es igual al área del triángulo rectángulo.
III)
En un triángulo rectángulo, tomando como diámetro la hipotenusa se construye exteriormente una semicircunferencia y tomando como diámetro los catetos se construyen semicircunferencias que se cortan sobre la hipotenusa.
El área de la región del triángulo rectángulo es igual a la diferencia de las áreas de las regiones de las dos lúnulas que se forman.
PROBLEMAS RESUELTOS
PREGUNTA 1 :
La alumna Estela dibuja y pinta un semicírculo de 12cm de radio. Determina el área (en cm2) que pintó dicha alumna.
A) 70𝛑
B) 76𝛑
C) 80𝛑
D) 64𝛑
E) 72𝛑
RESOLUCIÓN :
.png)
Rpta. : "C"
PREGUNTA 2 :
En el gráfico, el perímetro de la región sombreada es (24+3π). Calcula el área de su región si ABCD es un rectángulo.
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 3 :
Calcular el área (en cm2) de la región comprendida entre un círculo y el triángulo inscrito a este, de lados: 7cm, 24cm y 25cm (considere 𝜋=3).
A) 468,75
B) 384,75
C) 256,14
D) 318,25
E) 418,32
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 4 :
Si la longitud de una circunferencia es igual al perímetro de un cuadrado, el área que limita la región de la circunferencia es A y el área del cuadrado es B. Calcula B/A
A) 4/𝛑
B) 2/𝛑
C) 𝛑/2
D) 𝛑/4
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 5 :
Se tienen dos circunferencias circunscritas a dos hexágonos regulares. Si sus radios miden 4 y 8, calcule la relación de áreas de las regiones determinadas entre las circunferencias y sus polígonos regulares inscritos.
A) 1/4
B) 1/2
C) 1/8
D) 1/6
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 6 :
En la figura, O es punto medio del diámetro AC. Si las áreas de las regiones sombreadas son 𝕊1=7m2 y 𝕊2=41m2, halle el área del sector circular DOC.
A) 35 m2
B) 45 m2
C) 48 m2
D) 34 m2
E) 36 m2
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 7 :
Se tiene un triángulo equilátero de área 3√3u2. Determine el área de la región circular circunscrita a dicho triángulo
A) 2𝛑
B) 3𝛑
C) 6𝛑
D) 4𝛑
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 8 :
Se tiene un sector circular cuyo ángulo central es 2𝛑/5 rad . Calcula la relación de áreas de dicho sector y el círculo al cual pertenece.
A) 2/5
B) 1/4
C) 1/6
D) 1/5
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 9 :
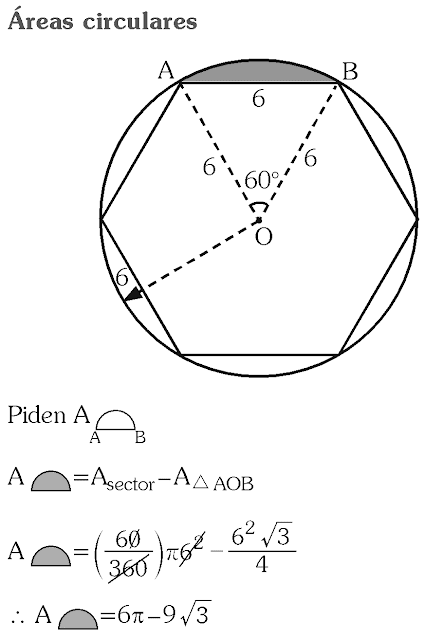
En un hexágono regular inscrito en una circunferencia de radio 6 u, calcula el área de uno de los segmentos circulares determinados por un lado del hexágono regular y la circunferencia.
A) 7π – 6√3
B) 6π – 9√3
C) 8π – 9√3
D) 9π – 6√3
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 10 :
En una circunferencia de radio 2 se inscribe un rectángulo cuyo lado menor es 2. Calcule el área de la región determinada entre dos lados consecutivos del rectángulo y la circunferencia.
A) 𝛑 − √3
B) 2(𝛑 − √3)
C) √3 (𝛑 − √3)
D) 4√3 (𝛑 − √3)
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 11 :
Si ABCD es un rectángulo inscrito en la semicircunferencia de radio igual a 2cm, calcula el área de la región sombreada. (“θ” está en radianes).
A) 2θ–sen2θ
B) 4θ–5senθ
C) 5θ–2senθ
D) 3θ–4senθ
RESOLUCIÓN :
Rpta. : "A"
PROBLEMA 1 :
Calcule el área de la región triangular sabiendo que el producto de sus lados es igual a 160 u3 y el circunradio mide 4 u.
A) 10 u2
B) 12 u2
C) 14 u2
D) 15 u2
E) 20 u2
PROBLEMA 2 :
En un triángulo rectángulo el cateto menor mide 7 m y la mediana relativa a la hipotenusa mide 12,5 m. Calcule el área de la región triangular.
A) 56 m2
B) 64 m2
C) 72 m2
D) 84 m2
E) 85 m2
PROBLEMA 3 :
En un triángulo rectángulo la circunferencia inscrita divide a la hipotenusa en dos segmentos que miden 4 y 6 m. Calcule el área de la región triangular.
A) 24 m2
B) 12 m2
C) 15 m2
D) 18 m2
E) 6 m2
PROBLEMA 4 :
Se tiene un triángulo ABC inscrito en una circunferencia de diámetro AC = 8√3 m; si AB=12m, calcule el área de la región triangular ABC.
A) 16 m2
B) 18 m2
C)16√3 m2
D) 24 m2
E) 24 3 m2
PROBLEMA 5 :
El diámetro AB de una circunferencia mide 25 m. Se traza la cuerda AP, cuya proyección ortogonal sobre el diámetro AB mide 9 m. Calcule el área de la región triangular APB.
A) 300 m2
B) 150 m2
C) 100 m2
D) 75 m2
E) 125 m2
PROBLEMA 6 :
Calcule el área de una región cuadrada inscrito en una semicircunferencia de 5√5 m de radio.
A) 25 m2
B) 49 m2
C) 64 m2
D) 81 m2
E) 100 m2
PROBLEMA 7 :
Cuando se alarga 20 m una cuerda que da la vuelta a un cuadrado, el cuadrado que se puede rodear tiene 445 m2 más que el primero. ¿Cuál es la longitud inicial de la cuerda?
A) 42 m
B) 126 m
C) 210 m
D) 84 m
E) 168 m
PROBLEMA 8 :
Calcule el área de una región rombal si su diagonal menor mide 12 cm y su perímetro es igual al de una región cuadrada de área 64 cm2.
A) 2 u2
B) 24√6 u2
C) 26 u2
D) 14√7 u2
E) 24√7 u2
PROBLEMA 9 :
Si a la diagonal mayor de un rombo se le quita 4 m, el área disminuye en 6 m2 y si a la diagonal menor se le agrega 4 m, el área aumenta en 30 m2. Calcule el área de la región rombal inicial.
A) 45 m2
B) 22,5 m2
C) 30 m2
D) 50 m2
E) 25 m2
PROBLEMA 10 :
Calcule el área de una región trapecial cuyas bases miden 4 m y 16 m, y sus diagonales 10 m y 14 m.
A) 44 m2
B) 8√66 m2
C) 360 m2
D) 4√33 m2
E) 240 m2
