TABLAS Y GRÁFICOS ESTADÍSTICOS PROBLEMAS RESUELTOS PDF
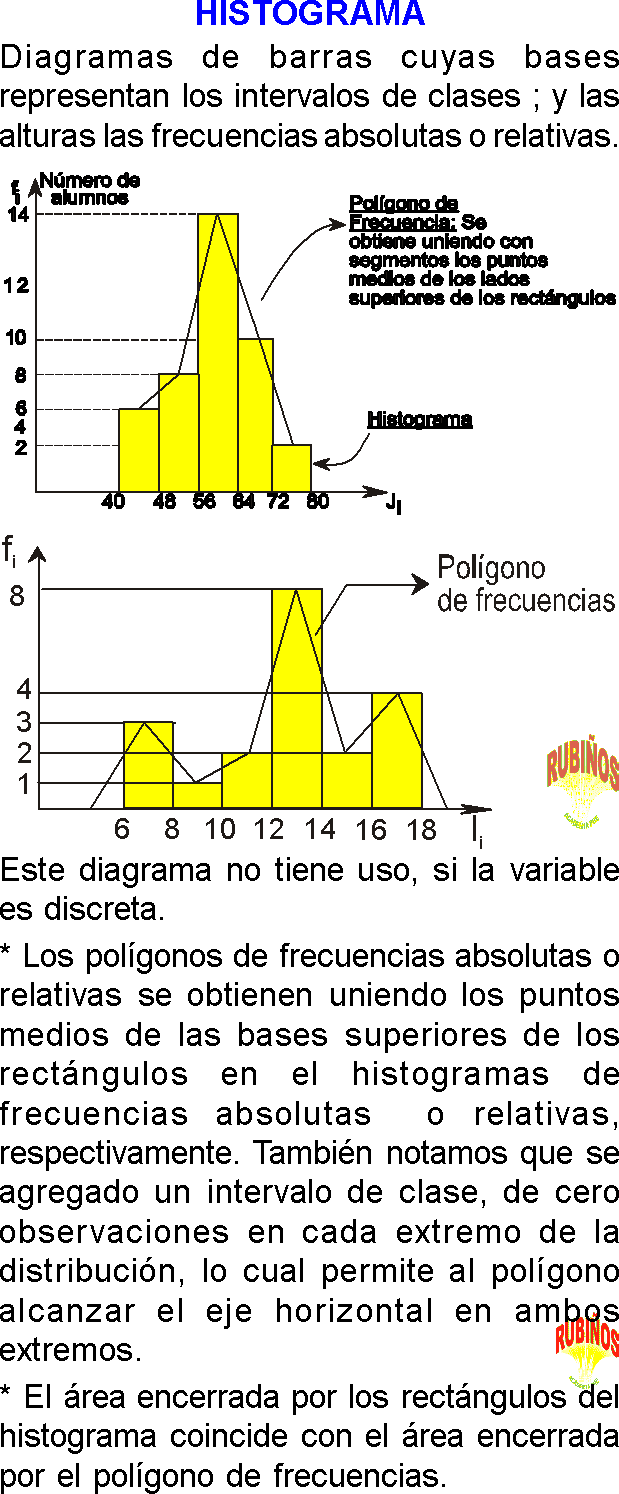
¿QUÉ SON GRÁFICOS ESTADÍSTICOS ?
Los gráficos estadísticos son herramientas que permiten mostrar información organizada y sintetizada, la cual se analiza e interpreta para sacar conclusiones.
Para analizar un conjunto de datos es conveniente organizarlos utilizando tablas y gráficas.
Éstas técnicas representan medios visuales que permiten entender modos de comportamiento y tendencias en los datos.
Existen varios tipos de gráficas o representaciones gráficas, que se utilizan de acuerdo al objetivo que se persigue y al tipo de información presentada.
- CLIC AQUÍ Ver GRÁFICAS DE SECTORES CIRCULARES
- Ver DIAGRAMAS DE BARRAS POLÍGONO DE FRECUENCIAS
- Ver DIAGRAMA ESCALONADO OJIVA
- Ver TABLAS DE DISTRIBUCIÓN DE FRECUENCIAS
- Ver ANÁLISIS DE GRÁFICAS ESTADÍSTICAS
- Ver ESTADÍSTICA TEORÍA Y EJERCICIOS RESUELTOS
- Ver ESTADÍSTICA NIVEL BÁSICO
- Ver ESTADÍSTICA FULL PROBLEMAS RESUELTOS
- Ver PRACTICA DE ESTADÍSTICA CON RESPUESTAS
- Ver VARIABLES ESTADÍSTICAS
- Ver MEDIDAS DE TENDENCIA CENTRAL
- Ver MEDIDAS DE DISPERSIÓN
PRESENTACIÓN GRÁFICA
Los gráficos son muy utilizados por los periodistas para presentar datos en la televisión y periódicos, son de utilidad para los médicos, ingenieros, administradores, economistas, psicologos , profesores, etc.
Ya que permiten observar el comportamiento de una muestra con respecto a alguna característica de un solo vistazo.
Algunas gráficas, para diagramar la distribución de los datos son : diagrama de barras, histogramas, polígonos de frecuencias, diagrama de sectores, pictogramas, pirámides de población ,...,etc.
PREGUNTA 2 :
La siguiente gráfica muestra los datos obtenidos cuando se preguntó a un grupo de personas por su tipo de película favorita. Cada persona solo votó por un solo tipo de película. En base a ello, señale la alternativa que presenta la secuencia correcta después de determinar si la proposición es verdadera (V) o falsa (F).
I. El porcentaje de los que eligieron Acción o Terror es 36,7% aproximadamente.
II. La razón de los que eligieron Drama a Suspenso es 4:3.
III. El total de los que eligen ya sea Suspenso, Acción o Terror son más de la mitad del total de encuestados.
A) VFV
B) FVV
C) VVV
D) FVF
E) FFF
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 3 :
Se tiene la siguiente tabla:
¿Cuál de las siguientes alternativas es correcta?
A) La diferencia porcentual entre reses y ovejas es la mitad de la diferencia porcentual entre caballos y ovejas.
B) El 25% de total son reses.
C) El número de reses es el 60% del número de ovejas.
D) La diferencia entre la cantidad de reses y cabras es el 30% del total de animales.
E) El número de reses es el 40% del número de ovejas.
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 4 :
El siguiente gráfico muestra el número de pacientes atendidos en una sala de emergencias. De acuerdo al área de emergencias y de acuerdo al genero, indica la afirmación correcta.
A) En cada área, el número de mujeres es mayor al número de hombres.
B) El número de intoxicados representa menos del 30 % del total.
C) La quinta parte del total eran mujeres heridas.
D) Los hombres son más del 50% del total.
E) Los hombres son del 30% del total.
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 5 :
El gráfico muestra el número de defunciones confirmadas por COVID-19 y según mes de deceso en Lima durante el año 2020. Señale la alternativa que presenta la secuencia correcta después de determinar si la proposición es verdadera (V) o falsa (F).
I. El mayor incremento de defunciones en forma porcentual del mes de abril al mes de mayo fue de 155% aproximadamente.
II. A partir del mes de junio el número de defunciones ha ido disminuyendo todo el año.
III. Entre los meses de octubre a diciembre hubo más defunciones que en el mes de agosto.
A) VVV
B) VFF
C) FFF
D) VFV
E) FVF
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 6 :
El siguiente cuadro muestra la producción de petróleo de los diez mayores productores a nivel mundial, en barriles por día.
¿Qué porcentaje del total representa la producción de petróleo del mayor productor a nivel mundial?
A) 37,4%
B) 28,72%
C) 41,36%
D) 30,72%
E) 31,95%
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 7 :
El siguiente pictograma representa el número de viviendas construidas en Lima durante los años del 2018 al 2020. En base a ello, señale la alternativa que presenta la secuencia correcta después de determinar si la proposición es verdadera (V) o falsa (F).
I. El porcentaje de disminución de viviendas del año 2018 al 2020 es del 28,67% aproximadamente.
II. El total de viviendas construidas entre los años 2018 a 2020 es de 320 000.
III. El número de viviendas construido el 2020 es la mitad de las construidas el 2018.
A) FVV
B) FFV
C) VFV
D) FFF
E) FVF
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 8 :
La siguiente tabla de frecuencias obtiene la cantidad de votos a favor y en contra acerca de un referéndum en una población de 710 personas agrupadas por rango de edad en años. Señale la alternativa que presenta la secuencia correcta después de determinar si la proposición es verdadera (V) o falsa (F).
I. El porcentaje de personas total que están a favor del referéndum y cuya edad es al menos de 61 años es del 36%.
II. El porcentaje de personas que están en contra y en el rango de 26 a 60 años es de 22% redondeado al entero más próximo.
III. Si los votos válidos excluyen a los indecisos entonces el porcentaje de los votantes de 18 a 25 años es del 21 % de los votos válidos aproximadamente.
A) FFF
B) VVV
C) FVF
D) VFV
E) FVV
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 9 :
Javier quiere iniciar un negocio de venta de electrodomésticos, para esto consulta a su amigo Fernando, quien ya tiene un negocio similar, acerca de sus ventas en los últimos meses. Fernando le proporciona la siguiente tabla.
¿Cuál es el número de artículos que espera vender Javier, en promedio, en su primer mes de trabajo?
A) 767
B) 816
C) 720
D) 800
E) 600
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 10 :
El gráfico muestra los resultados de un examen tomado a 10 alumnos: alumno 1, alumno 2,..., alumno 10. Si la nota para aprobar es mayor o igual a 15. ¿Cuantos aprobaron?
A) 4
B) 5
C) 6
D) 7
E) 3
RESOLUCIÓN :
Del gráfico se observa que los que tienen 15 o más son los alumnos: 2, 4, 5, 7, 9 y 10
Total 6 alumnos
Rpta. : "C"
PREGUNTA 11 :
El siguiente cuadro muestra las ventas (en miles de soles) en las tiendas A, B, C y D de una compañía, en todo el verano de 2022.
Calcula la diferencia entre el mayor y menor promedio obtenido por las tiendas A, B, C y D. (En miles de soles).
A) 15
B) 20
C) 10
D) 18
E) 12
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 12 :
De la pregunta anterior , ¿cuánto le falta a C (miles de soles), para que sea el 25% del total de ventas del verano?
A) 80
B) 120
C) 90
D) 95
E) 40
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 13 :
Los sueldos de un obrero (en el año 2020) trimestralmente fueron:
¿Cuál debe ser el valor de x para que el promedio sea S/.950?
Además durante el año 2021 sus sueldos trimestralmente aumentaron como sigue:
¿Cuál es el sueldo promedio durante el 2021?
A) S/. 1025
B) S/. 1050
C) S/. 1020
D) S/. 1100
E) S/. 1075
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 15 :
Dado el siguiente gráfico de sectores referente al presupuesto mensual de un trabajador.
Si gana mensualmente S/2600. ¿Cuánto gastó en educación y en otras actividades?
A) 720 y 240
B) 720 y 280
C) 760 y 280
D) 780 y 260
E) 780 y 280
RESOLUCIÓN :
PREGUNTA 16 :
El siguiente gráfico muestra el sueldo mensual de 40 personas.
¿Qué porcentaje de personas tienen un sueldo menor que S/ 3000?
A) 40,5 %
B) 40 %
C) 30 %
D) 17,5 %
E) 36 %
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 17 :
En un centro de investigación, se hace el seguimiento sobre el alto nivel de THN de un grupo de pacientes, que se indica en el gráfico anterior. Indique la alternativa correcta.
A) De marzo a abril se presenta la mayor variación porcentual.
B) De enero a febrero disminuye un 25%.
C) Con respecto a febrero, en marzo hay un incremento de 50% de los pacientes con alto índice de THN.
D) En enero se presenta el mayor número de pacientes con THN.
B) De enero a febrero disminuye un 45%.
RESOLUCIÓN :
Rpta. : "C"
Enunciado (PREGUNTAS 18 ; 19 y 20 )
El siguiente gráfico muestra el número de panes producidos por una panadería en la mañana, al medio día y en la tarde a lo largo de la semana. Se sabe además que el número total de panes producidos por día es 1300 de los cuales el 30% son de yema y el resto francés.
PREGUNTA 18 :
¿Cuál es el número de panes franceses que producen un lunes por la tarde?
A) 120
B) 91
C) 150
D) 130
E) 87
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 19 :
Halle el promedio del número de panes franceses que se producen por día en la mañana.
A) 540
B) 564
C) 456
D) 654
E) 546
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 20 :
Halle el promedio del número total de panes que se producen al medio día.
A) 489,2
B) 476,4
C) 498,3
D) 495,2
E) 456,4
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 21 :
Si los candidatos A, B, C, D participan en una elección. El siguiente gráfico solo muestra los resultados de los candidatos A, B, C.
Si el total de votos fue de 510, de los cuales 10 votos no fueron considerados.
¿Cuál fue el candidato de menor aceptación?
A) A
B) B
C) C
D) E
E) D
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 22 :
Si el siguiente cuadro muestra la tasa de mortalidad, de cada quinquenio, en tanto por mil.
¿Cuál de las siguientes variaciones es correcta?
A) La variación de la tasa de mortalidad del 1er y 2do quinquenio fue de 15%
B) La variación de la tasa de mortalidad rural del 2do al 3ero quinquenio fue de 20%
C) La variación de la tasa de mortalidad del 3ero al 4to quinquenio fue de 18%
D) La variación de la tasa de mortalidad urbana del 3ero al 4to quinquenio fue de 12%
E) La variación de la tasa de mortalidad del 3ero al 4to quinquenio fue de 32%
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 23:
La afluencia de turistas en tres zonas, A, B y C, de cierta zona turística de Arequipa en el 2015 fue de 50 000 personas y en el 2016 aumentó en 20%, como se muestra en los diagramas. Se desea conocer en cuánto aumentó la afluencia de turistas en la zona B.
A) 300
B) 3500
C) 4000
D) 4200
E) 4500
Rpta. : "C"
PREGUNTA 24:
El gráfico adjunto muestra los resultados de una encuesta acerca de las preferencias del público respecto a los candidatos a la alcaldía de cierto distrito de Lima. Señale la alternativa correcta, después de determinar si la proposición es verdadera (V) o falsa (F).
I. El candidato A tiene el 25 % de preferencia.
II. El 37,5% de preferencia la tiene B.
III. C, D y E suman igual porcentaje que B.
A) VVV
B) VVF
C) VFV
D) VFF
E) FVV
Rpta. : "A"
PREGUNTA 25 :
Un estudio para aprobar el presupuesto de un municipio revela que el gráfico de barras mostrado y lo que opinan acerca del mismo los concejales pertenecientes al partido amarillo, al partido verde y los independientes. ¿Cuál es el mayor número? en contra sin opinión
A) Número de amarillos a favor del presupuesto.
B) Número de verdes en contra del presupuesto.
C) Número de independientes sin opinión.
D) A, B, C son iguales.
E) Se requiere información adicional.
RESOLUCIÓN :
Piden determinar qué número de personas es mayor; sin embargo, en los datos solo se tiene información de porcentaje; por ejemplo, hay un 50 % de amarillos, pero al no tener el total de amarillos esta cantidad no se puede determinar y menos comparar con las otras.
Por lo tanto, se requiere información adicional.
Rpta. : "E"
PREGUNTA 26 :
El siguiente diagrama de barras muestra la distribución de las edades de un grupo de alumnos.
Si se sabe, además, que hay 1120 personas que tienen más de 13 años, determina la respuesta correcta.
A) Hay 1200 personas de 13 años.
B) Hay 760 personas menores de 12 años.
C) Hay 500 personas de más de 14 años.
D) Hay 3000 personas en total.
E) Hay 2860 personas en total.
RESOLUCIÓN :
Gráfico de barras Número de personas mayores de 13 años:
n+100+n+60+n+60=1120
⇒ 3n+220=1120
⇒ 3n=900
⇒ n=300
Analizando claves:
A) Personas de 13 años: n+600=900... (Falso)
B) Personas menores de 12 años: 2n+160=760... (Verdadero)
C) Personas mayores de 14 años: 2n+120=720... (Falso)
D) Total de personas: 7n+1180=3280... (Falso)
Rpta. : "B"
PREGUNTA 27 :
El siguiente gráfico muestra la cantidad de alumnos que ingresaron en el examen POP 2022.
¿Cuál de las siguientes afirmaciones es correcta?
A) En ciencias, los ingresantes hombres representan el 55 %.
B) El 48 % del total de ingresantes son mujeres.
C) Los ingresantes a educación representan el 7 % del total.
D) En letras, el 60 % de los ingresantes son mujeres.
E) El 24 % del total de ingresantes son mujeres.
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 28:
El gráfico muestra una figura que apareció en un diario de una ciudad. En él se indica la preferencia por el noticiero central de 5 canales de televisión según una muestra aleatoria en un año determinado.
¿Cuál(es) de las siguientes afirmaciones es(son) verdadera(s)?
I. De acuerdo a la muestra, el noticiero central con menor probabilidad de ser visto es TV5.
II. El gráfico muestra exactamente la realidad de la preferencia de los noticieros de esta ciudad.
III. Aproximadamente, un cuarto de la muestra no ve noticieros centrales de estos 5 canales.
A) solo I
B) solo II
C) I y II
D) I y III
E) I, II y III
RESOLUCIÓN :
I. De acuerdo a la muestra, el noticiero central con menor probabilidad de ser visto es TV5.
Con referencia a la muestra el noticiero central TV5 tiene menos preferencias y, por ende, menor probabilidad de ser visto con respecto a los otros 4 noticieros.
La proposición I es verdadera.
II. El gráfico muestra exactamente la realidad de la preferencia de los noticieros de esa ciudad.
La encuesta muestra una aproximación (no exacta) de la realidad, la cual tendrá un margen de error.
La proposición II es falsa.
III. Aproximadamente un cuarto de la muestra no ve los noticieros centrales de estos 5 canales.
No ven los noticieros de esos canales =
100% – (26,3% + 22,3% + 11,5% + 9,8% + 5,2%) = 24,9%
La proposición III es verdadera.
Rpta. : "D"
PREGUNTA 30:
La municipalidad de San Isidro presentó el número de multas a los establecimientos comerciales durante el segundo semestre del año 2016. De la siguiente gráfica de líneas:
Diga qué enunciados son verdaderos.
I. En diciembre hubo el mayor número de multas.
II. En los meses consecutivos de septiembre - octubre y noviembre - diciembre hubo un descenso en las multas.
III. El porcentaje de multas del mes de septiembre fue 28 %.
A) I
B) II
C) III
D) I y II
E) II y III
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 31 :
La siguiente gráfica muestra el número de postulantes (en cientos) a una universidad durante el periodo 2011 a 2021. En base a ello, señale la alternativa que presenta la secuencia correcta después de determinar si la proposición es verdadera (V) o falsa (F).
I) El porcentaje de disminución de postulantes del año 2019 al 2020 es del 37%, aproximadamente.
II) De acuerdo al gráfico solo hay dos periodos anuales cuando el número de postulantes ha aumentado.
III) El promedio de postulantes entre los años 2011 y 2015 es de 3960.
A) VVV
B) FVV
C) FVF
D) FFF
E) VFV
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 32:
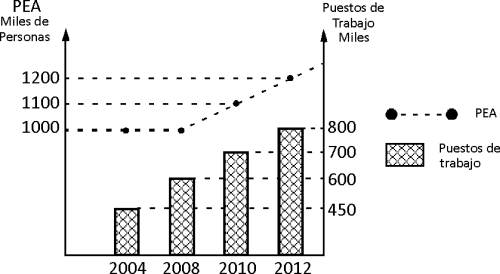
El gráfico muestra la estadística de los últimos años de la población económicamente activa (PEA) y de los puestos de trabajo.
En base a la información, determine las afirmaciones correctas.
I. La tasa de crecimiento de la PEA y de los puestos de trabajo, del 2008 al 2012 ha sido igual.
II. La tasa de crecimiento de los puestos de trabajo ha sido mayor a la PEA en los últimos 8 años.
III. El desempleo se reduce en los últimos 4 años.
A) solo I
B) solo II
C) solo III
D) I, II y III
E) I y III
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 33 :
El gráfico muestra la temperatura promedio de dos ciudades en grados Fahrenheit a lo largo de un año. Señale la alternativa que presenta la secuencia correcta después de determinar si la proposición es verdadera (V) o falsa (F).
I. El número de meses en que la temperatura en la ciudad A ha sido mayor que en la ciudad B es 4.
II. El número de meses en que tanto la temperatura en la ciudad A y de ciudad B es por lo menos 60 °F es 6.
III. El menor temperatura de la ciudad A se dio en el mes de diciembre.
A) VFV
B) VFF
C) FVV
D) FVF
E) FFF
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 34 :
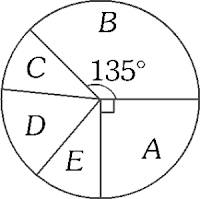
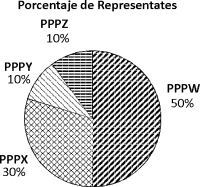
En el Congreso están elegidos 130 representantes que conforman 4 grupos con los porcentajes indicados en el gráfico circular.
El día de una votación están ausentes algunos representantes como se muestra el cuadro.
La votación obtenida después de un largo debate fue como se muestra en el gráfico de barras, en porcentaje referido al número de presentes.
Todos los presentes votan, que representan el 100 %
Con la información brindada, señale el valor de verdad (V) o falsedad (F) de las siguientes afirmaciones:
I. De la agrupación PPPW ese día solo votaron 61 representantes.
II. Si todos los miembros del grupo PPPW votó a favor, 27 miembros de otros grupos también votaron a favor.
III. Todos los miembros presentes de la agrupación PPPZ votaron a favor.
A) VVV
B) VVF
C) VFF
D) FFF
E) FFV
RESOLUCIÓN :
Rpta. : "C"