FRACCIONES EJERCICIOS RESUELTOS PDF RAZONAMIENTO MATEMÁTICO

Seguramente mas de un vez hemos visto o escuchado en alguna tienda, en los 
medios de comunicación o al hablar con algunas personas expresiones como las siguientes: 
► Comeré la octava parte de la pizza
► Hoy almorcé un cuarto de pollo a la brasa
► Véndame medio kilogramo de papa
► Compra una gaseosa de litro y medio
Todas estas expresiones hacen referencia a las fracciones. Como podemos ver están presentes en nuestro hacer cotidiano.
GUIA DE EJERCICIOS CON RESPUESTAS
PREGUNTA 1 : 
Un comerciante compró un artefacto gastando los 3/7 de su capital, quedándole de éste S/.360. ¿De qué capital disponía el comerciante? 
A) S/.430 
B) S/.530 
C) S/.630 
D)S/.480 
E) S/.690 
Rpta. : "C"
PREGUNTA 2 : 
Juan tiene cierta cantidad de dinero y gasta la cuarta parte, luego gasta la quinta parte de lo que queda y por último regala la sexta parte de lo que queda, quedándose con S/. 90. ¿Cuánto le hubiese quedado si solo gastaba la novena parte? 
A) S/. 80 
B) S/.90 
C) S/.100 
D) S/.120 
E) S/.160 
Rpta. : "E"
PREGUNTA 3 : 
Indicar la fracción equivalente a 3/7 sabiendo que la diferencia de los cuadrados de sus términos es 360 ; dar como resultado la diferencia de sus términos. 
A) 16 
B) 24 
C) 64 
D) 12 
E) 8 
Rpta. : "D"
PREGUNTA 4 : 
Gasté los 2/7 de lo que no gasté y aún me queda S/.45 más de lo que gasté, ¿cuánto tenía? 
A) S/.27 
B) 72 
C) 81 
D) 108 
E) 180 
Rpta. : "C"
PREGUNTA 5 : 
Se reparte caramelos entre 4 niños; al primero le tocó 1/4 del total; al segundo 1/8 ; al tercero 1/12 y al cuarto le tocó 6 caramelos más que a los otros 3 juntos. ¿Cuántos caramelos le tocó al segundo? 
A) 42 
B) 39 
C) 9 
D) 56 
E) 36 
Rpta. : "C"
PREGUNTA 6 : 
Una Editorial tiene para la venta un cierto número de libros, vende primero las 3/5 partes y después le hacen un pedido de los 7/8 de lo que le queda pero antes de servir este pedido se le inutilizan 240 libros, por lo tanto al enviar todos los libros útiles que le quedan, sólo se cubre los 4/5 de la cantidad pedida. ¿Qué cantidad de libros se vendieron? 
A) 1760 
B) 2500 
C) 1200 
D) 4800 
E) 7200 
Rpta. : "A"
PREGUNTA 7 : 
Gasté los 3/5 de lo que no gasté y aún me quedan S/.60 más de lo que gasté. ¿Cuánto tenía? (en soles) 
A) 150 
B) 190 
C) 200 
D) 250 
E) 240 
Rpta. : "E"
PREGUNTA 8 : 
¿Cuántos tercios hay en 5/2? 
A) 7 
B) 2/15 
C) 7,5 
D) 2,5 
E) 6/5 
Rpta. : "C"
PREGUNTA 9 : 
¿En cuántos 96 avos es menor 1/3 que 1/2 ? 
A) 24 
B) 16 
C) 48 
D) 12 
E) 28 
Rpta. : "B"
PREGUNTA 10 : 
Bruno tiene un huerto de manzanos. Cada año Bruno vende a José toda la cosecha. Sin embargo, este año Bruno pensó aprovechar una parte de la cosecha para fabricar mermelada y sidra. Repartió la cosecha de la siguiente manera: la mitad para José, la tercera parte para preparar mermelada y la sexta parte para la sidra. ¿Quedó parte de la cosecha sin repartir? 
A) Sí, quedó la tercera parte. 
B) Sí, quedó la mitad. 
C) No quedó nada. 
D) Sí, quedó la sexta parte. 
E) Sí, quedó una doceava parte. 
Rpta. : "C"
PREGUNTA 11 : 
Una bola de ping-pong cae desde una altura de 108 cm. sobre una mesa de mármol. Cada vez que toca a la mesa, rebota y se eleva a una altura igual a la tercera parte de la altura desde la cual cayó. ¿A qué altura se elevará la bola después de haber tocado a la mesa por tercera vez? 
A) 5 cm 
B) 4 
C) 3 
D) 9 
E) 12 
Rpta. : "B"
PREGUNTA 12 : 
De un reservorio se sacan 800 litros, si habían los 2/3 y quedan 2/5 . ¿Cuántos litros se necesitan para terminar de llenarla? 
A) 1200 
B) 1500 
C) 8000 
D) 7200 
E) 4800 
Rpta. : "E"
PREGUNTA 13 : 
Dos tercios de los profesores de un colegio son mujeres, 12 de los profesores varones son solteros, mientras que los 3/5 de los mismos son casados. ¿Cuál es el número de docentes? 
A) 80 
B) 90 
C) 60 
D) 70 
E) 50 
Rpta. : "B"
PREGUNTA 14 : 
Luis gastó 4/5 de su dinero. Si en lugar de los 4/5 sólo hubiera gastado los 3/8 , tendría ahora 272 soles más de lo que tiene, ¿cuántos soles tenía Luis? 
A) 650 soles 
B) 600 
C) 640 
D) 630 
E) 620 
Rpta. : "C"
PREGUNTA 15 : 
Al dejar caer al suelo una pelota cada vez que rebota se eleva a una altura igual a los 2/3 de la altura anterior. Si después de 3 rebotes alcanza una altura de 80cm. ¿De qué altura cayó inicialmente? 
A) 350 cm 
B) 270 cm 
C) 400 cm 
D) 150 cm 
E) 200 cm 
Rpta. : "B"
PREGUNTA 16 : 
Si me fui a un parque de diversiones y gasté un quinto de mi dinero, luego gasté un cuarto de lo que me quedaba y finalmente gasté un tercio de lo que tenía. Si para ir a casa el taxi me cobró 10 soles y me quedé con 14 soles, ¿cuánto gasté en total? 
A) S/. 60 
B) S/. 56 
C) S/. 46 
D) S/. 54 
E) S/. 36 
Rpta. : "C"
PREGUNTA 17 : 
En un recipiente lleno de leche se extrae un quinto de lo que no se extrae y luego se vuelve a extraer 1/5 de lo que quedaba, quedando en el recipiente 64 ml. ¿Cuántos mililitros había en el recipiente? 
A) 80mL 
B) 90mL 
C) 96mL 
D) 112m 
E)120 mL 
Rpta. : "C"
PREGUNTA 18 : 
Un cartero dejó 1/5 de las cartas que lleva en una oficina, los 3/8 en un Banco, si aún le quedaban 34 cartas por distribuir, ¿cuántas cartas tenía para distribuir? 
A) 60 
B) 80 
C) 70 
D) 120 
E) 90 
Rpta. : "B"
PROBLEMAS RESUELTOS
PREGUNTA 1 : 
En el siguiente cuadrilátero, ¿qué parte del total está sombreado? 
A) 5/16 
B) 5/12 
C) 3/16 
D) 3/4 
E) 3/8 
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 2 : 
En un salón de clase de 54 alumnos, 36 son varones. ¿Qué fracción son mujeres? 
A) 1/3 
B) 1/2 
C) 1/4 
D) 1/5 
E) 2/3 
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 3 :
Un comerciante compró cierta cantidad de ceniceros y luego vendió la sexta parte de dicha cantidad. Si, al guardar lo restante, rompió accidentalmente 55 ceniceros y aún le quedaron intactos 5/8 del total de ceniceros comprados, ¿cuántos ceniceros compró el comerciante? 
A) 288 
B) 240 
C) 312 
D) 264 
RESOLUCIÓN :
Rpta. : "D"
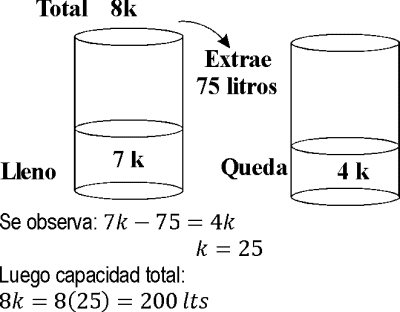
PREGUNTA 4 : 
El tanque de agua de un edificio está lleno hasta 7/8 de su capacidad. Si se vacían 75 litros, aún queda la mitad. ¿Cuál es la capacidad del tanque? 
A) 50 litros 
B) 200 litros 
C) 100 litros 
D) 250 litros 
E) 300 litros 
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 5 : 
Una persona gasta su dinero de la siguiente manera: los 2/3 en alimentos, los 3/5 del resto en pasajes, los 5/6 del resto en ropa y lo que le queda, que es S/ 24 los ahorra. ¿Cuánto destina para sus alimentos? 
A) S/. 720 
B) S/. 740 
C) S/. 680 
D) S/. 640 
E) S/. 760 
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 6  : 
Un grifo tiene un tanque que contiene gasolina hasta los 4/11 de su capacidad. Cuando llega un camión surtidor y agrega 340 galones de gasolina, la cantidad de gasolina que ahora contiene el tanque alcanza el 75 % de su capacidad. A partir de ese instante, se vende la totalidad de gasolina que tiene el tanque a razón de 20 soles el galón. ¿Cuál fue el ingreso que se obtuvo? 
A) S/.12 560 
B) S/.13 120 
C) S/.13 200 
D) S/.10 290 
RESOLUCIÓN :
Rpta. : "C"

PREGUNTA 7 : 
Magaly llegó tarde al cine; exactamente cuando la película había avanzado 1/8 del total. Seis minutos después, llegó Sonia y solo vio los 4/5 del total. Si la película empezó a las 4:00 p. m., ¿a qué hora terminó? 
A) 5:00 p. m. 
B) 5:10 p. m. 
C) 5:30 p. m. 
D) 5:15 p. m. 
E) 5:20 p. m. 
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 8 :
Un padre decide repartir de su rebaño todas sus vacas entre sus cuatro hijos. El primero recibió la mitad del rebaño, el segundo la cuarta parte, el tercero la quinta parte y el último las siete últimas vacas. ¿Cuántas vacas había en el rebaño? 
a) 100 
b) 70 
c) 140 
d) 150 
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 9 :  
Un comerciante vende mascarillas; el primer día vende la mitad, el segundo día vende la tercera parte del resto y el tercer día vende la quinta parte del nuevo resto. Si al final le quedan 120 mascarillas, ¿cuántas mascarillas vendió el segundo día? 
a) 68 
b) 75 
c) 95 
d) 80 
e) 70 
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 10 : 
A un examen solo asistieron 4/5 del número total de alumnos matriculados. De los que asistieron aprobaron los 3/4 y desaprobaron 25. ¿Cuántos alumnos matriculados no asistieron a dicho examen? 
A) 25 
B) 75 
C) 100 
D) 125 
E) 150 
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 11 : 
Se ha tomado cierta parte de un vaso lleno de agua. La tercera parte de lo que queda es igual a la mitad de lo que ha tomado. Si toma la cuarta parte de lo que queda, ¿qué fracción del total es lo que le queda? 
A) 3/20 
B) 9/20 
C) 7/20 
D) 11/20 
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 12 : 
Una estatua G hecha de bronce pesa 500 kg. Si se construyera una estatua P con el mismo material y cuyas dimensiones fueran todas las quintas partes de G , ¿cuánto pesaría P ?
A) 4 kg
B) 10 kg
C) 8  kg
D) 5  kg
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 13 : 
Un abuelo reparte una herencia entre sus 3 nietos, al primero le da los 2/5 y al segundo la mitad. Si al tercero de tocó S/18 700, ¿cuál era la herencia repartida? 
A) S/180 000 
B) S/187 000 
C) S/216 000 
D) S/360 000 
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 14 : 
En una caminata 1/5 del tiempo transcurrido equivale a 3/5 del tiempo que falta transcurrir. ¿Qué tiempo ha transcurrido hasta el momento si la caminata es de 9 horas? 
A) 6 h 
B) 6 h 15 min 
C) 6 h 30 min 
D) 6 h 45 min 
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 15 : 
¿Cuánto se debe sumar al numerador de la fracción 2/9 para que sea equivalente a los 4/5 de 10/12? 
A) 3 
B) 4 
C) 5 
D) 6 
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 16 : 
Se observa que cierto tipo de café pierde 1/5 de su peso al tostarlo. Comprando café verde a 12 soles cada kilogramo, ¿a cómo deberá venderse el kilogramo de café tostado para ganar 1/10 del precio de compra? 
A) 18,00 soles 
B) 17,50 soles 
C) 16,50 soles 
D) 15,50 soles 
E) 14,00 soles 
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 17 : 
En un colegio, donde asisten más de 150 alumnos, pero menos de 200, se observa que los 3/35 de ellos son extranjeros. ¿Cuántos alumnos asisten al colegio? 
A) 140 
B) 175 
C) 210 
D) 150 
E) 200 
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 18 :
El producto de los términos de una fracción es 120. Si se le suma uno al numerador y se le quita uno al denominador, ambos términos serían iguales. Da como respuesta la suma de dichos términos. 
a) 11 
b) 10 
c) 12 
d) 22 
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 19 : 
Se tiene una tela rectangular de 8 dm de ancho. Cada vez que se lava se reduce 1/16 de su ancho y 1/5 de su largo. ¿Cuánto medía su largo (en metros), si luego de ser lavada tiene un área de 60 000 cm²? 
A) 8 
B) 12 
C) 10 
D) 15 
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 20 : 
Al efectuar la siguiente operación 
Se obtiene A/B . 
Halle (A+B) 
A) n²+2n+1 
B) 2 
C) n+3 
D) n+1 
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 21 : 
Ruth tenía cierta cantidad de dinero y decide gastarlo. Gastó 3/7 en comprar un vestido, luego gastó las 3/5 partes del dinero restante en comprar un pantalón; por último gastó la mitad de lo que le queda en comprar una blusa. Si todavía le quedan S/40, ¿cuánto dinero tenía? 
A) S/ 350 
B) S/ 400 
C) S/ 450 
D) S/ 500 
E) S/ 550 
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 22 :
Dados los números p y q definidos como 
p = 3/7  – 4/9
q = 11/5 – 4 
es posible afirmar que 
A) p es positivo y q es negativo. 
B) p es negativo y q es positivo. 
C) p es positivo y q es positivo. 
D) p.q es negativo. 
E) p.q es positivo. 
RESOLUCIÓN :
Rpta. : "E"

Ejercicios resueltos de examen de admisión a la Universidad