DERIVADAS TEORÍA Y EJEMPLOS BASICOS PDF
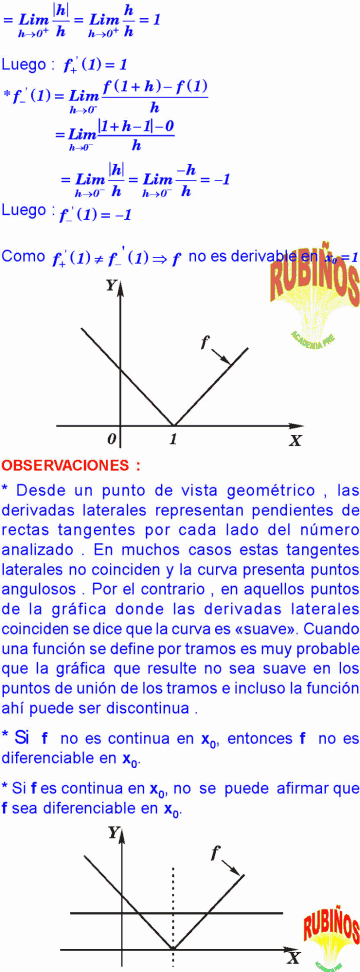
Indica la verdad o falsedad de las siguientes afirmaciones : a) , entonces f ’(x) = –2x + 4 b) Si , entonce c) Si f(x) = x3 – 2x , entonces f ’(1) = 1 d) f(x) = senx + 5x , entonces Calcular las derivadas de : a)f(t) = 12 – 3t4 + 4t6 b)k(x) = (2x2 – 4x + 1)(6x – 5) c) f(x) = (4x – 5) / (3x + 2) d) f(x) = 1 / (1 + x + x2 + x3) Indicar la verdad o falsedad de las siguientes afirmaciones : a) La recta tangente a una curva y = f(x) en el punto (x0, y0) , corta a la gráfica de la función necesariamente en otro punto . Justifica tu respuesta graficamente . b) La recta tangente a una curva y = f(x) en punto (x0 , y0) no corta a la gráfica de la función en otro punto . c) La recta secante a una curva y = f(x), corta a la gráfica de f en dos o más puntos. La siguiente proposición es verdadera o falsa: Existen funciones que tienen la misma derivada . Justifica algebraicamente tu respuesta . Por ejemplo considera f(x)= x + 1 y g(x)= x – 3. Da un par de ejemplos más . Indica la verdad o falsedad de la siguiente afirmación : Si f es una función diferenciable, entonces f(x) y f(x) + c tienen la misma derivada . Indica la verdad o falsedad de la siguiente proposición : Si una función f es continua en x0, entonces será diferenciable en x0 . Justifica tu respuesta. Demuestre que es diferenciable en todo su dominio . Demuestra que f(x) = cosx es diferenciable sobre . Dada la función a) ¿Para qué valor de “a”, f es continua en todo su dominio? b) ¿Existe (3) y (3) ? c) ¿Es f diferenciable en ? Dada la función , halla: a) f’(1) b)f’(8) c)f’(x0) Halla la pendiente de la recta tangente a la curva definida por f(x) = 2x + senx en el punto abscisa Halla la pendiente de la recta tangente a la curva definida por f(x) = x3 + 3 en el punto de ordenada y0 = 4 . Dada la función definida por : a) Determina si f es continua en x = 1. b) Determina si f es diferenciable en x = 1. Dada la función f(x) = x|x| a) ¿Es continua en x = 0? b) ¿Es derivable en x = 0? Dada la función definida por : a) ¿Es f diferenciable en x = –1? b) ¿Es f continua en x = –1? Sea f(x) = 15x2 + (65 – 10x)2, halla los máximos y mínimos relativos de f , si existen. Dada la función , halla los valores extremos relativos de f , si existen. Efectúa la gráfica de