FÓRMULAS DE CONVERSIÓN DE MEDIDAS ANGULARES EJERCICIOS RESUELTOS PDF TRIGONOMETRÍA

APRENDIZAJES ESPERADOS

• Reconocer la fórmula general de conversión y usarla convenientemente en los problemas que involucran número de grados sexagesimales (S), número de grados centesimales (C) y número de radianes (R) que contiene un ángulo.

• Interpretar correctamente los problemas de enunciado literal, para su posterior resolución.

FÓRMULA GENERAL DE CONVERSIÓN

Es la relación existente entre los números que representan la medida de un ángulo en los tres sistemas conocidos.

PRIMERA PRACTICA

EJERCICIO 1 :

Convertir 36º a radianes

EJERCICIO 2 :

Convertir 54° al sistema centesimal.

EJERCICIO 3 :

Convertir 54° al sistema centesimal.

EJERCICIO 4 :

Convertir 1 rad al sistema sexagesimal.

EJERCICIO 5 :

Convertir 40° al sistema radial.

EJERCICIO 6 :

Hallar la medida de un ángulo en radianes, si su número de grados centesimales (C) y sexagesimales (S) cumplen: C – S = 4

EJERCICIO 7 :

Siendo “S” y “C” lo conocido para un mismo ángulo , tal que:

S = n + 1

C = n + 3

¿cuál es la medida sexagesimal del ángulo?

EJERCICIO 8 :

Calcula la medida de un ángulo en radianes si:

S + C = 95

a) 𝛑/ rad

b) 𝛑/2 rad

c) 𝛑/3 rad

d) 𝛑/4 rad

e) 𝛑/5 rad

Rpta. : "D"

EJERCICIO 9 :

Sabiendo que S y C representan lo convencional para un ángulo “α” y además:

C – S = 4

Halla la medida circular de “α”

a) 𝛑/4 rad

b) 𝛑/2rad

c) 𝛑/5rad

d) 𝛑/8rad

e) 𝛑/9rad

Rpta. : "C"

EJERCICIO 10 :

Determina la medida circular de un ángulo que verifica :

S=x – 10

C=x + 10

Siendo S y C lo conocido.

a) 𝛑rad

b) 𝛑/2rad

c) 𝛑/4rad

d) 𝛑/6rad

e) 2𝛑rad

Rpta. : "A"

EJERCICIO 11 :

Calcula un ángulo en radianes,

Si: 2S+5C = 13,6

a) 𝛑/10 rad

b) 𝛑/100 rad

c) 𝛑/1000 rad

d) 𝛑/50 rad

e) 𝛑/40 rad

Rpta. : "B"

EJERCICIO 12 :

Determina la medida circular de un ángulo que verifica :

S + C + R = 383,1416

Siendo S, C y R lo conocido.

a) 𝛑rad

b) 𝛑/2rad

c) 𝛑/4rad

d) 2𝛑rad

e) 𝛑/6rad

Rpta. : "A"

SEGUNDA PRACTICA

PREGUNTA 1 :

Señale el equivalente de 40^g en el sistema sexagesimal.

a) 18°

b) 20°

c) 24°

d) 36°

e) 42°

PREGUNTA 2 :

¿Cuál es la razón geométrica entre la suma de los números de grados sexagesimales y centesimales de un ángulo no nulo, con su número de grados centesimales?

a) 1,9

b) 2,1

c) 3,8

d) 5,7

e) 0,9

PREGUNTA 3 :

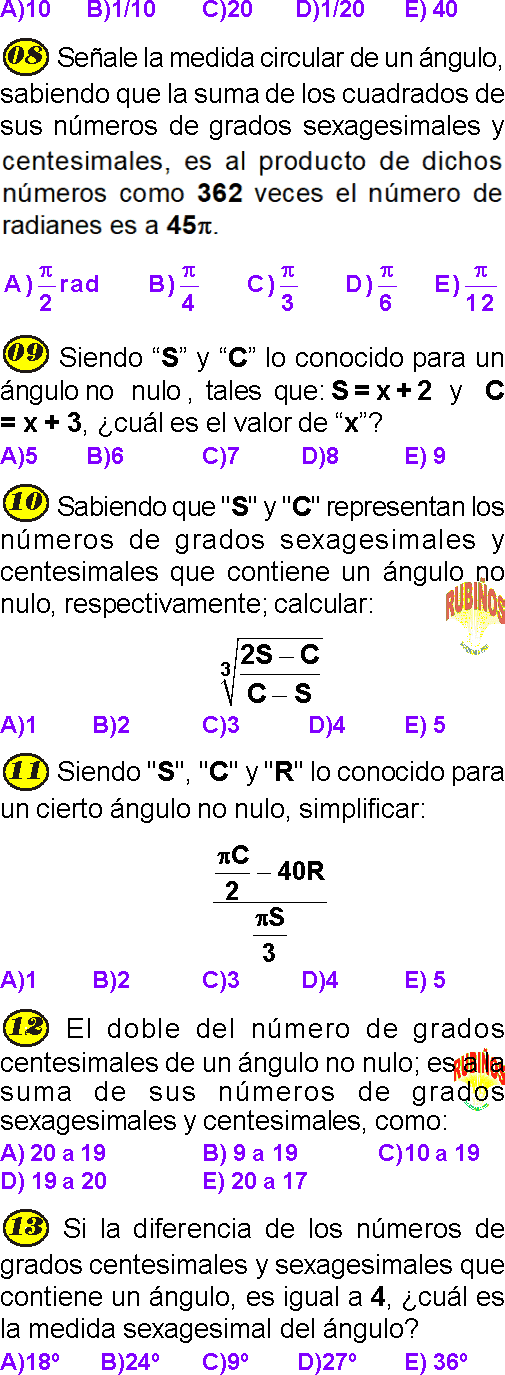
Señale la medida circular de un ángulo, sabiendo que la suma de los cuadrados de sus números de grados sexagesimales y centesimales, es al producto de dichos números como 362 veces el número de radianes es a 45𝛑.

A) (𝛑/2)rad

B) (𝛑/4)rad

C) (𝛑/3)rad

D) (𝛑/6)rad

E) (𝛑/12)rad

PREGUNTA 4 :

Siendo “S” y “C” lo conocido para un ángulo no nulo , tales que:

S = x + 2

C = x + 3

¿cuál es el valor de “x”?

a) 5

b) 6

c) 7

d) 8

e) 9

PREGUNTA 5 :

El doble del número de grados centesimales de un ángulo no nulo; es a la suma de sus números de grados sexagesimales y centesimales, como:

A) 20 a 19

B) 9 a 19

C) 10 a 19

D) 19 a 20

E) 20 a 17

PREGUNTA 6 :

Si la diferencia de los números de grados centesimales y sexagesimales que contiene un ángulo, es igual a 4, ¿cuál es la medida sexagesimal del ángulo?

a) 18º

b) 24º

c) 9º

d) 27º

e) 36º

PREGUNTA 7 :

Señale la medida radial de un ángulo, si el doble de su número de grados sexagesimales excede a su número de grados centesimales, en 16.

A) (𝛑/18)rad

B) (𝛑/20)rad

C) (𝛑/10)rad

D) (𝛑/36)rad

E) (𝛑/72)rad

PREGUNTA 8 :

Señale la medida sexagesimal de un ángulo tal que:

S = n + 1

C = n + 4

siendo “S” y “C” lo conocido para dicho ángulo.

a) 18°

b) 9°

c) 27°

d) 15°

e) 36°

PREGUNTA 9 :

Señale la medida centesimal de un ángulo tal que:

S = 7n + 1

C = 8n;

Siendo “S” y “C” lo conocido para dicho ángulo.

A) 10g

B) 20g

C) 30g

D) 40g

E) 50g

PREGUNTA 10 :

Señale la medida radial de un ángulo sabiendo que el producto de los números que representan su medida en los tres sistemas conocidos, es igual a 𝛑/6.

A) (𝛑/3)rad

B) (𝛑/5)rad

C) (𝛑/6)rad

D) (𝛑/60)rad

E) (𝛑/30)rad

TERCERA PRACTICA

PREGUNTA 1 :

La diferencia de los recíprocos de los números de grados sexagesimal y centesimal de un mismo ángulo es igual a su número de radianes que contiene el ángulo dividido por 6𝛑. Halle aproximadamente, el valor de dicho ángulo en radianes.

A) 0,128

B) 0,181

C) 0,256

D) 0,362

E) 0,543

Rpta. : "A"

PREGUNTA 2 :

El número que representa el valor de un ángulo en el sistema centesimal es mayor en 11 unidades al número que representa al mismo ángulo en el sistema sexagesimal. Entonces, el valor del ángulo, en radianes, es:

A) 0,172

B) 0,727

C) 2,750

D) 1,727

E) 3,172

Rpta. : "D"

PREGUNTA 3 :

Un estudiante observa que las agujas de su reloj forman un ángulo, cuyo número de grados sexagesimales y centesimales son iguales, luego la hora que indica el reloj podría ser:

A) 3:15 a.m.

B) 6:30 a.m.

C) 6 a.m.

D) 12 m.

E) 12:30 p.m.

Rpta. : "D"

PREGUNTA 4 :

Sean dos ángulos, el primero mide p grados sexagesimales y el segundo q grados centesimales. La diferencia numérica de estas medidas es 15 . Si la suma de estos ángulos en el sistema sexagesimal es 129 , los ángulos, tal como estaban medidos originalmente, son:

A) 30 y 15

B) 45 y 30

C) 60 y 45

D) 75 y 60

E) 90 y 75

Rpta. : "D"

PREGUNTA 5 :

Siendo S y C los números que expresan la medida de un mismo ángulo en los sistemas sexagesimal y centesimal que cumple 20 < 3C – 2S < 60. Halle la medida del mayor ángulo en radianes ,tal que S y C son números enteros.

A) (𝛑/10)rad

B) (𝛑/5)rad

C) (𝛑/4)rad

D) (𝛑/3)rad

E) (𝛑/2)rad

Rpta. : "B"

PREGUNTA 6 :

Determine el ángulo entre 100° y 220° que sea coterminal con 1285°.

A) 45°

B) 55°

C) 65°

D) 75°

E) 205°

Rpta. : "E"

PREGUNTA 7 :

La suma de las inversas de los números que representan a dos ángulos suplementarios en grados sexagesimales es 10 veces la diferencia de las inversas de los números que representan a dichos ángulos en el sistema centesimal. Halle el mayor de ellos en el sistema sexagesimal.

A) 100°

B) 105°

C) 110°

D) 115°

E) 120°

Rpta. : "A"

PREGUNTA 8 :

La medida de un ángulo en los sistemas sexagesimal y centesimal están representadas por dos números pares consecutivos. Halle la medida de dicho ángulo en radianes.

A) (𝛑/12)rad

B) (𝛑/10)rad

C) (𝛑/6)rad

D) (2𝛑/3)rad

E) (5𝛑/3)rad

Rpta. : "B"

PREGUNTA 9 :

Los números que representan la medida de un ángulo en los sistemas sexagesimal y centesimal son x¹⁰⁰ y x¹⁰⁰+1 respectivamente. Halle el valor del complemento del ángulo , expresado en radianes.

A) (7𝛑/20)rad

B) (8𝛑/20)rad

C) (9𝛑/20)rad

D) (10𝛑/22)rad

E) (11𝛑/3)rad

Rpta. : "C"

PROBLEMAS RESUELTOS

PREGUNTA 1:

Si “S” y “C” son los números de grados sexagesimales y centesimales respectivamente de un mismo ángulo, halle su medida en el sistema radial, sabiendo que: